「文字式の利用（説明・等式の変形）」応用問題の解き方も紹介

中学２年数学で学習する「文字式の利用」について、式による説明の仕方、等式の変形のやりかた、文字式の利用の応用問題・カレンダーの問題などをわかりやすく解説しています。

「文字式の利用（説明・等式の変形）」 応用問題の解き方も紹介のPDF（27枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 数の性質を説明してみよう（式の説明）
• 式を変形してみよう（等式の変形）
• 文字式の利用の応用問題
• まとめ

数の性質を説明してみよう（式の説明）

「数の性質を説明する」って、そもそもどういうことだろう。
たとえば、テストではこんなふうに問題が出るんだ。

「説明しなさい」なんて言われると、たとえばこの問題を説明するとしたら

たろう

１＋２＋３＝６
６は３の倍数だから成り立つよ！

・・・というように、実際の数字を使って説明したくなってしまうよね。

でも、もし一番小さい数字が、たとえば「３８１」だったらどうかな？

たろう

「３８１」か・・・。
３８１＋３８２＋３８３＝１１４６
１１４６は３の倍数だからやっぱり成り立つよ！

たしかに、こんなふうに特定のパターンが決まっているのであれば、計算式をひとつひとつ書いてあげることで説明することができるけれど、実際には数字は無限にあるため、全てが成り立つような説明をすることって不可能だよね。

くまごろう

全部のパターンをひとつひとつ計算式で説明するなんて、不可能だよね。

そこで、役に立つのが中学数学で使うようになった「文字」なんだ。
文字を使えば、全てのパターンについて説明することができるようになるんだよ。

それでは、文字を使って説明する方法を確認しよう。

（１）文字を使う数量の表し方を確認しよう。

今回の問題では、『連続する３つの整数』や『３の倍数』という言葉がでてきたね。これらは、全て文字式を使って表すことができるんだ。

●連続する３つの整数を文字で表す方法

まずは、連続する３つの数を数字だけで考えてみよう。
例えば、≪１、２、３≫　や　≪７、８、９≫　がイメージできたかな？

では、これを文字を使って表してみよう。

連続する３つの整数のうち、一番小さい整数を『ｎ』とした時に、残りの２つの整数はどんな風に表現できるだろう？

≪１、２、３≫　≪７、８、９≫をそれぞれの一番小さい数字を基準に考えると

のこりの２つの整数はそれぞれ、
『一番小さい数＋１』、
『一番小さい数＋２』
という形になっていることに気づいたかな？

この性質を利用すると、一番小さい整数が『ｎ』だった時、残りの２つの整数は、

ｎ＋１、ｎ＋２

と表すことができるね。

●３の倍数

３の倍数も実際の数字で考えてみよう。
たとえば、≪３、９、１８、２１≫などがイメージできたかな？

それぞれの数字を分解して考えてみると…

全て、≪３×□≫の形になっているね。
文字式で表す時も、同じように３×ｎのように表すことができるよ。

このように、問題文に出てくる数量のことを、文字を使ってどのように表現できるかを確認するところからはじめよう！

この「問題文に出てくる数量を、文字を使って表すことができるか」がかなり重要なポイント。
むずかしそうに感じるかもしれないけれど、たくさんの問題を解いているうちに、だいたいパターンやコツがつかめてくるから安心してね。

（２）説明の手順を覚えよう

さて、問題文に出てくる数量のことを、文字を使って表現できたら、次はそれを使って「説明」をしなくてはいけないよ。

例えるなら、材料（文字で表現した数量）がそろったので、問題文のとおりに料理をしていくイメージ。

「説明」には、書き方の「型」のようなものがあるので、これもたくさん問題を解いて、説明の書き方に慣れていく必要があるよ。

では、実際にさっきの問題を使って「説明の書き方」について確認しよう。

手順➀　使う文字式について説明する

もう一度問題文を見てみるよ。

問題文の最初から料理していこう。
今回の問題ではまず『連続する３つの整数』とあるので、これを文字で表現することを説明するよ。

このように、書き始めるよ。
これは、他のパターンでも同じように書き始めるから、覚えておこう。

手順➁　問題文にある「計算」をする

問題文の中には、必ず『計算』するところが隠れているよ。

今回の問題では『和』と書かれているね！『和』は、『足し算』をした時の答えのことだから、「連続する３つの整数を足す」ということだね。

これを揃えた材料（文字と数字）で表すと、

このように計算することができるね。

説明する問題の中にある計算は、簡単な計算が多いよ。

手順③　問題に書かれている『〇〇になること』の形へ変形する

問題の中に、『〇〇になること』を説明しなさい、と書かれているのが説明問題の特徴だよ。

説明問題では、計算した答えを『〇〇になること』の形に変形する必要があるんだ。

今回は、『３の倍数になること』と書かれているね。
②で解いた計算の答えを３の倍数の形に変形するよ。

３の倍数は、『３×□』の形で表すことができるから、今回の　≪３ｎ＋３≫　も同じように変形すると、

このように表現することができるよ。

３ｎ＋３を『３×（　　　）』の形に変形するところがポイントだよ。この形に変形するのが苦手な人は、途中式にある

３×ｎ＋３×１

と分解した形を書くと整理しやすくなるよ。

手順④　式と言葉をつなげて説明を完成させる

ここまでくればもうゴールは近いよ。

①から③まで書くことができたら、あとはそれぞれをつなげて、説明を完成させよう。

また、①から③まで書いたあと、毎回書くキーワードがあるから、それも確認しよう。

途中にある、

ｎ＋１は整数だから、３（ｎ＋１）は３の倍数になる

これは、説明の時に必ず書くキーワードなんだ。

このフレーズは書き忘れないように注意しよう。書き忘れた場合には、減点される可能性があるので注意！

説明問題は、フレーズや数量の表現の仕方など暗記の要素が多い単元だよ。
最初は、書き方を確認しながら覚えるまで繰り返し取り組もう。

それでは、ほかの問題のパターンも見てみよう。

２けたの自然数の問題もよく出題されるパターンだよ。

２けたの自然数がどのように表されるか、そして、一の位の数字と十の位の数字を入れかえた数の表し方について確認しよう。

２けたの自然数とは、

３５、７３、９８のような数だね。

これらは、

と考えるんだ。

１０円玉と１円玉を使って数字を表現しているイメージを持ってもらえるといいね！
※３けたの自然数の場合は、１００円玉と１０円玉と１円玉と考えるようにしよう。

これを文字を使って表現すると、

このように表すことができるよ。

あとは、最初の問題と同じように、手順に沿って書き進めていこう。
※問題にある『差』は引き算をした時の答えだから、「引き算」をすればいいんだよ。

※「χ－ｙ」が整数になる理由・・・２けたの自然数の十の位の数である「χ」も、２けたの自然数の一の位の数である「ｙ」も整数だよね。
ということは、「χ－ｙ」は、「整数－整数」ということになる。
整数から整数を引くだけだから、答えはかならず整数になるよね。

※９（χ－ｙ）は９の倍数となる理由・・・「χ－ｙ」は整数なんだよね。
そうすると、９（χ－ｙ）は９×□とおなじことだから、かならず９の倍数になるよ。

１年生の時に学習した文字式の単元の知識（偶数や奇数など）も使うことがあるので、不安な人は復習をしておこう！

カレンダー問題

「カレンダー問題」は、文字式の利用でよく出る応用問題だよ。
カレンダーの性質を利用した問題について確認しよう。

問題

上にあるカレンダーは、ある月のカレンダーである。

上のカレンダーのように、縦２つ、横２つの正方形で囲んだとき、４つの数の和は４の倍数になることを説明しなさい。

まずは、赤い□で囲われた箇所を文字を使って表現してみよう。

上の例の場合

となっているので、これを参考にして、一番小さい数字をｎを使うと

と表すことができるね。これを元に、先ほどの問題と同じように説明を書き進めていこう。

カレンダーの問題も数量の表し方さえ間違えなければ、大丈夫！

ぜひチャレンジしてみよう！

式を変形してみよう（等式の変形）

文字式の問題では、式の形を変形する問題が出題されるんだ。
変形する、と聞くと難しそう……と感じる人もいるかもしれないけれど、実はみんな中学１年生の時にやったことのある知識で解くことができるよ！

じゃあ、早速問題を見てみよう！

問題にある『ｙについて解く』とは、どういうことか説明するね。

これは、式を『ｙ＝』の形に変形する、ということなんだ。
つまり中学１年生の時に習った、『方程式』と同じように解く問題ということなんだよ。
※方程式の時は、『χ＝』と変形したね！

実際に解くときの手順は、とてもシンプルだよ。

この手順を頭に入れて例題の解き方を見てみよう。

手順➀　移項する

最終的に『ｙ＝』の形にしたいから、ｙのついた項以外は、全て『＝』の右側に移項しよう。

移項する時のルールは、『移項した項の符号が変わる』だったね！
『＋のものは、－に』『－のものは、＋に』

このルールで、

と変形することができたね！

手順➁　『×（かける）』でくっついている数字は、『逆数を掛けて消す』

『ｙ＝』の形に変えるために、あと余計なものは、『４』だね！

『よし、じゃあこれを移項して…』というのはやってはいけない方法だよ。
移項をしていいのは、『＋』や『－』でくっついている時だけ！

『×（かける）』でくっついている場合には、逆数をかけて消す、と覚えておこう。

では、このルールで、４ｙ＝－２χ＋１３を『ｙ＝』の形に変形してみよう。

４ｙは、もともと４×ｙの『×』を省略した形だったね。
なので、４を消すためには、\(\frac{１}{４}\)をかけて消そう。

また、左側の項だけではなく、右側の項の全てに同じ数を掛けることも忘れずに！
右側の項は、『－２χ』と『＋１３』だね！このどちらにも\(\frac{１}{４}\)を掛けて、実際に計算をしていくと、

となるね！

ちなみに、教科書では両辺を同じ数で割って整理する、という解き方をしているよ。

この解き方でも同じ答えになるんだけれど、計算ミスをしないようにするためにも『今回説明した逆数をかける』がおすすめだよ！

では、次の問題に進もう！

この問題で、注意してほしいのは

ａｂが真ん中に書かれているけれど、これは分子（上側）にくっついている

ということなんだ。書き換えると……

\(\frac{２ａｂ}{３}\)＝８

これと同じ式だということなんだ。

では、ここから解き進めていこう！

この式は、全て『×（かける）』でくっついていることに気がついたかな？

つまり

\(\frac{２}{３}\)×ａ×ｂ＝８

ということだよ。

『×（かける）』でくっついている時は、逆数を掛けて消す

というルールなので、ｂ以外の逆数を考えてみよう。

なので、『ｂ＝』の形に変形するには、

\(\frac{３}{２}\)と\(\frac{１}{ａ}\)を両辺に掛けると解くことができるよ！

さあ、ここまでできたら、難問にチャレンジしてみよう！

分数だし、分子はごちゃごちゃしていて、よくわからない……となりそうだけど、一つひとつ整理して見ていくと、解くことができるよ！

まずは、みんなが気になる \(\frac{２χ－４ｙ}{３}\) について確認しよう。

この部分は、

をまとめた形なんだ。計算する時には、このバラバラの状態にするとミスなく解くことができるよ！

あとは、解き方のルールにしたがって解き進めればOK！

ちなみに答えは、 χ＝\(\frac{４ｙ＋１５}{２}\) のようにまとめた形でも正解だよ。

式の形を変形する問題は、ミスなく正確に解くことが重要だよ。
途中式を省略して、計算ミスをすることが無いように注意しよう！

文字式の利用の応用問題

これまで学習した内容を使って、応用問題にチャレンジしよう！

応用問題１

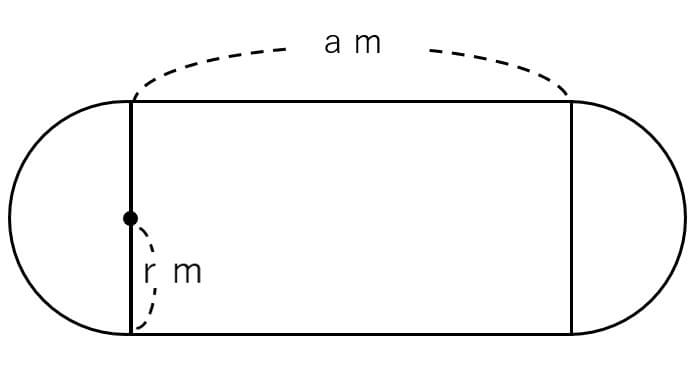
上の図のような、直線部分がａｍ、半円部分の半径がｒｍ、１周の長さが４００ｍのコースがあります。

このとき、コース１周の長さについて

２ａ＋２πｒ＝４００

という等式が成り立ちます。このとき、次の問に答えなさい。

（１）２ａ＋２πｒ＝４００をａについて解きなさい。

（２）（１）で変形した式を使って、半円部分の半径が２５ｍのときの直線部分の長さを求めなさい。

（１）ａについて解く、というのは『ａ＝』の形に変形する、ということだったね。

手順通りに解き進めれば、問題なく解くことができるよ。

（２）は（１）を解くことができれば、代入するだけで解くことができるよ。
今回の問題では、半径が２５ｍ、ということは、ｒ＝２５ということだよ。

※ちなみに、代入とは文字と数字を交換する、と覚えておこう。
今回の問題では、ｒと２５を交換すればＯＫだよ。

式の変形を使った問題だけれど、基本をマスターしていれば解くことができる問題だよ！

まずは、連続する３つの偶数を文字を使って表現しよう。

ちなみに、偶数とは２で割り切れる数、のことだよ。
具体的には、２、４、６、８、１０、、、の数字が偶数なんだ。

これを参考に、３つ連続した偶数を文字を使って表現してみよう。

使う文字を表現できたら、文字式の説明の手順で書き進めていこう。

６の倍数は、６×□の形にすることも忘れずに！

※連続する３つの偶数について、真ん中の数を２ｎとして、
２ｎ－２、２ｎ、２ｎ＋２と表現する方法もあるよ。解きやすい方を選ぶようにしよう！

応用問題３

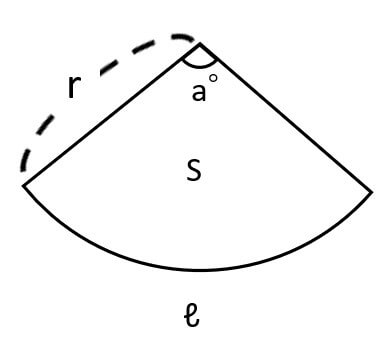
上の図のように、おうぎ形の半径をｒ、中心角をａ°とすると、弧の長さℓ、面積Ｓは、それぞれ次のように表すことができます。

ℓ＝２πｒ×\(\frac{ａ}{３６０}\)

S＝πｒ²＋\(\frac{ａ}{３６０}\)

この２つの式から、おうぎ形の面積Sは、

S＝\(\frac{１}{２}\)ℓｒ

と表されることを証明しなさい。

この問題は、パズルのように式を変形して証明をする問題なんだ。

数字や文字をうまくかけて、証明したい形へ変形してみよう。

問題で与えられた ℓ＝２πｒ×\(\frac{ａ}{３６０}\)

を変形して、証明したい S＝\(\frac{１}{２}\)ℓｒに近づけていこう。

証明したい式の右辺（イコールの右側）を見てみると

\(\frac{１}{２}\)ℓｒとなっているね。

これは、

ℓ＝２πｒ×\(\frac{ａ}{３６０}\)

この式に\(\frac{１}{２}\)ｒを掛けたら同じ形になることに気づけるかどうかがポイントだよ。

両辺に\(\frac{１}{２}\)ｒを掛けると

と変形することができるよ。

右辺に注目すると、

S＝πｒ²＋\(\frac{ａ}{３６０}\)

と同じ形になっていることに気づいたかな？

ここまできたら、あとは答えを書き進めて証明を完成させよう。

この証明で使われた、S＝\(\frac{１}{２}\)ℓｒの式は、実際におうぎ形の面積を求める計算に使うことができるよ。

式もシンプルだから、計算ミスの防止にもなる便利な公式だよ！

まとめ

文字式を利用した問題は、難しいと感じる人が多いんだ。

でも、出題パターンや解き方の手順が決まっているよ。

・等式の変形の手順

・説明問題の説明の手順

それぞれの解き方の手順を、何度も確認をして、マスターしよう！

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。

1. ないろ より:

   2024年6月20日 11:10 PM

   とても分かりやすかったです!!

   返信