対頂角・同位角・錯角とは？「平行線の性質」をわかりやすく解説

中学２年生の数学で学習する「対頂角」「同位角」「錯角」とはどういう位置関係の角なのか？それぞれ、どういう性質をもっているのか、平行な２つの線と交わる１つの直線が作る角の、対頂角・同位角・錯角はどういう性質をもっているのかをわかりやすく解説するよ。

対頂角・同位角・錯角とは？「平行線の性質」をわかりやすく解説のPDF（8枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

対頂角とは

図形の単元で使う角度には、色々な名前がついた角度があるんだけれど、最初は「対頂角たいちょうかく」について説明するね。

２つの直線が交わった時に、下の図のように４つの角度ができるよね。

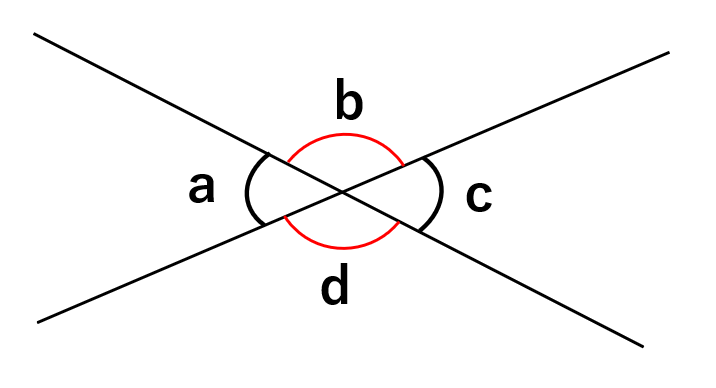
この時、「ａとｃ」「ｂとｄ」のように向かい合う角のことを対頂角と呼ぶんだ。

対頂角の角の大きさは必ず等しくなる、という性質があるよ。
図形の角度の計算問題でよく使う性質だから、確実に覚えておこう。

問題

下の図の角ａ、ｂ、ｃ、ｄの大きさを求めなさい。

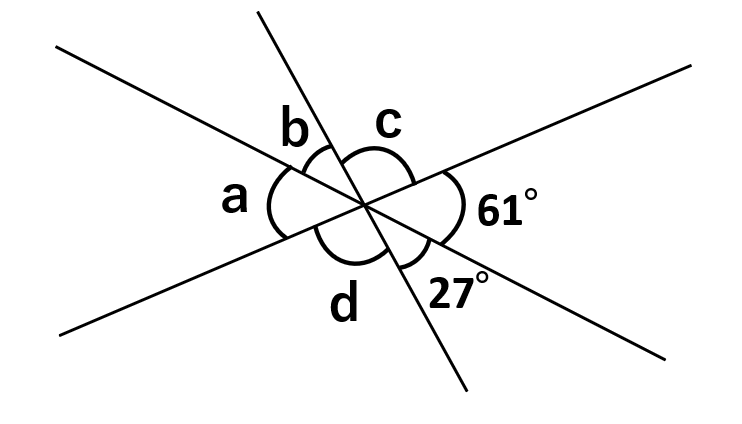
①∠ａと∠ｂの大きさ
∠ａと∠ｂは、それぞれの対頂角の大きさがわかっているね。
対頂角の大きさは等しくなるから、∠ａ＝６１°、∠ｂ＝２７°と求めることがでできるよ。

②∠ｃと∠ｄの大きさ
∠ｃと∠ｄは対頂角の関係だから、片方の大きさがわかればＯＫだよ。

∠ｄは「一直線が作る角の大きさは１８０°」という性質を使うと角の大きさを求めることができるよ。

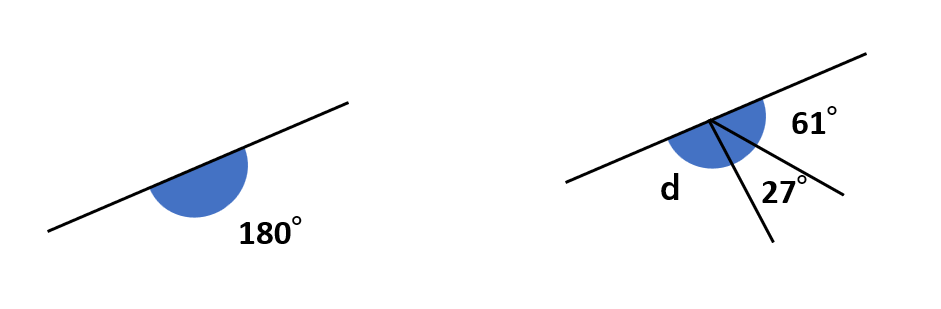
上の図のように考えると、∠ｄ＋２７°＋６１°＝１８０°となるから、∠ｄ＝９２°と求めることができるね。
∠ｃは∠ｄと同じ大きさだから、∠ｃ＝９２°となるよ。

同位角とは

次は「同位角どういかく」について確認していこう。
同位角は漢字の通り「同じ位置にある角」という意味なんだ。

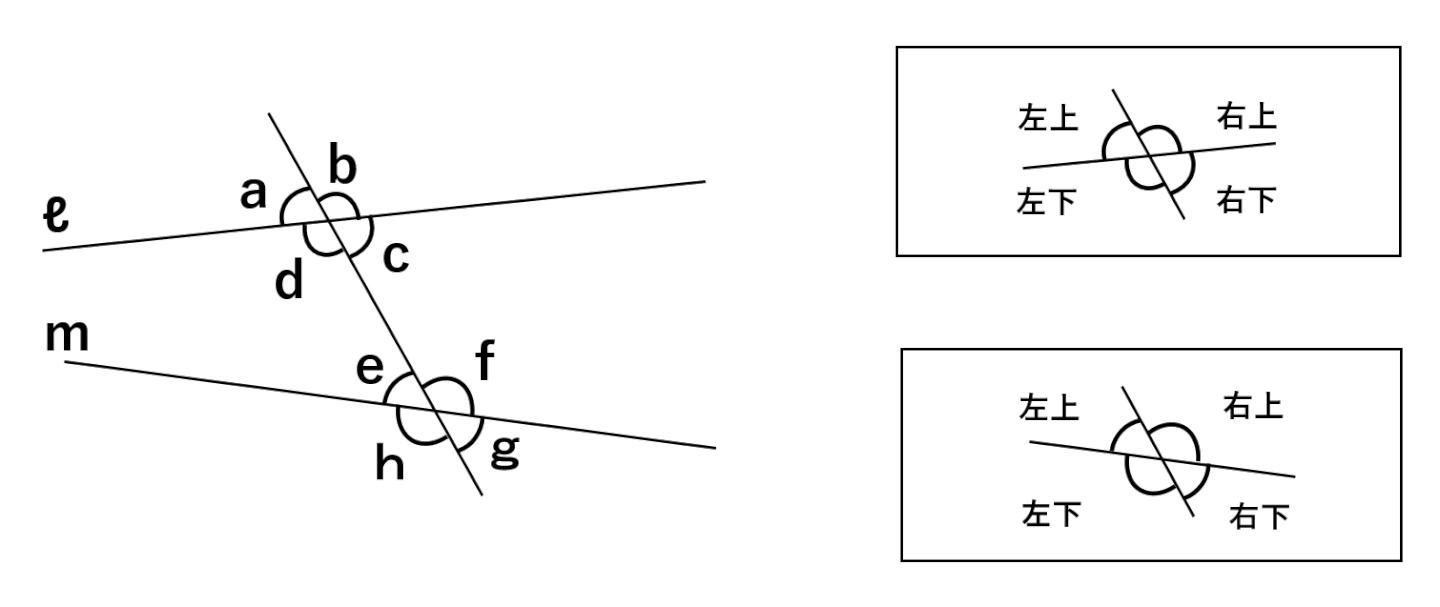
上の図の直線ℓと直線ｍに１つの直線が交わって作られる角の位置に注目してみよう。

直線ℓで作られる∠ａ、∠ｂ、∠ｃ、∠ｄは、∠ａが左上、∠ｂが右上、∠ｃが右下、∠ｄが左下にあることがわかるね。
直線ｍで作られる∠ｅ、∠ｆ、∠ｇ、∠ｈも同じように考えると、∠ｅが左上、∠ｆが右上、∠ｈが右下、∠ｇが左下にあるね。

この時、∠ａと∠ｅ（左上にある角）、∠ｂと∠ｆ（右上にある角）、∠ｃと∠ｇ（右下にある角）、∠ｄと∠ｈ（左下にある角）のように作られている位置関係が同じ角を同位角と呼ぶんだ。

錯角とは

次は「錯角さっかく」という角について確認しよう。

「目の錯覚さっかく」という言葉があるから、聞いたことがあると思った人がいるかもしれないけれど、漢字が違うから注意してね。

錯角も同位角と同じように、角の位置関係から呼ばれる角なんだけれど、少し複雑なんだ。

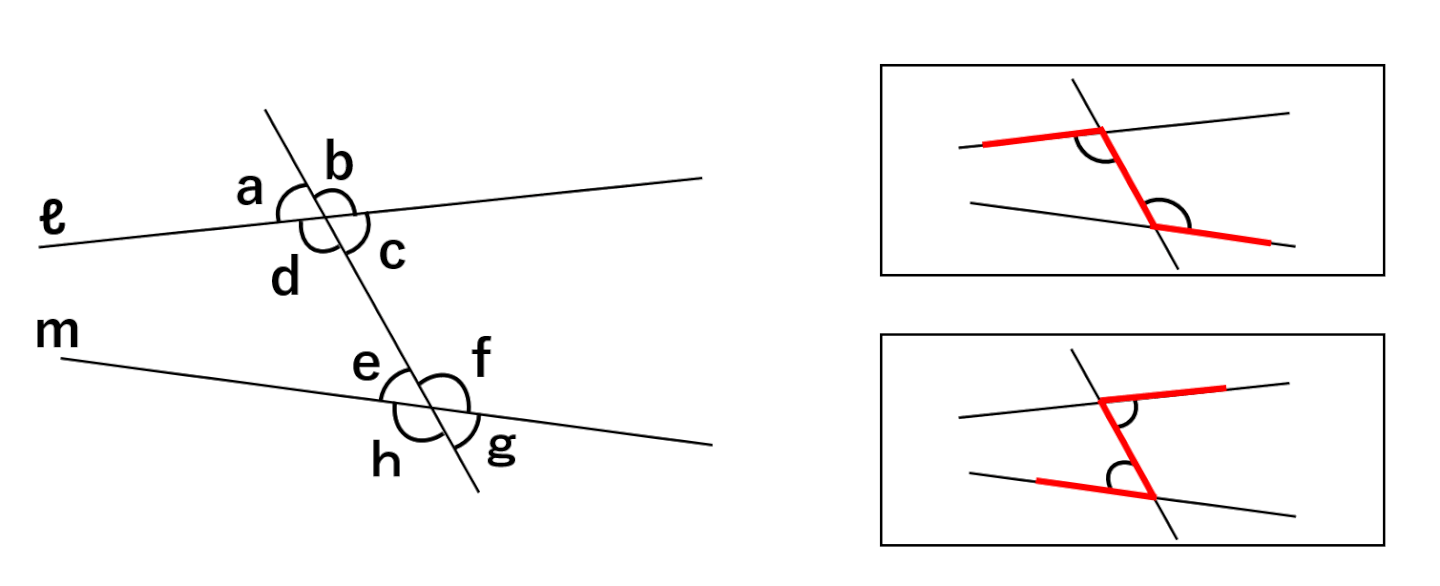
上の図で錯角の関係になっているのは、∠ｄと∠ｆ、∠ｃと∠ｅだよ。

錯角を見つけるコツとして、錯角の位置関係はアルファベットのZと逆Zの形をしたところにできる角の位置関係と覚えておこう。

錯角は同位角のように、わかりやすい関係ではないため錯角を見つけるのに苦労するかもしれないけれど、中学２年生の図形単元ではよく出てくるから、問題演習を通して慣れていこう。

平行線の性質

これまで説明してきた同位角・錯角について、直線ℓと直線ｍが平行な時について考えてみよう。

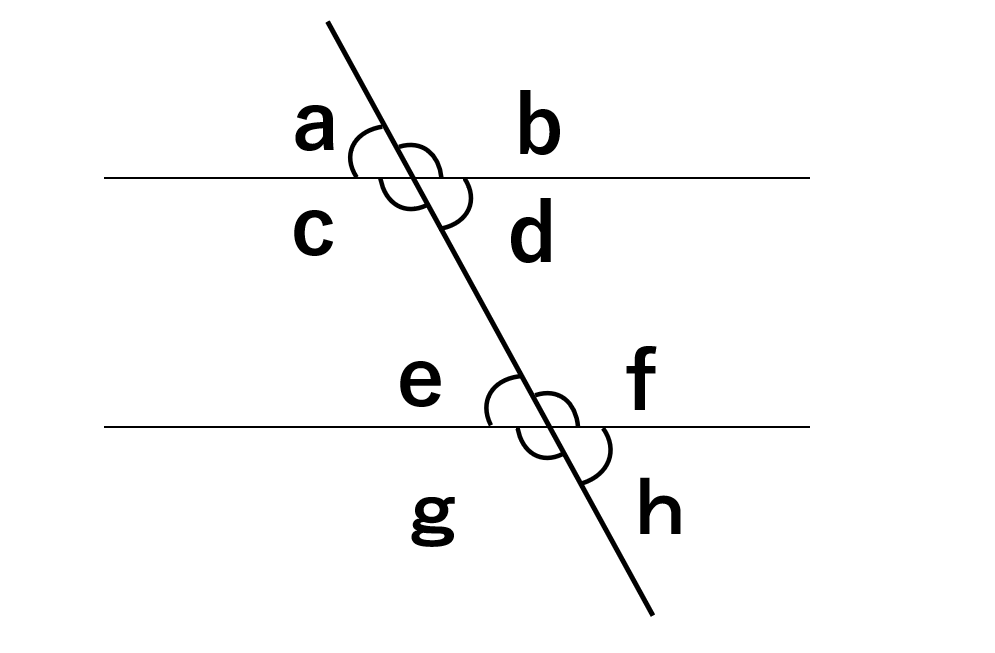
上の図を見ると、少し予想できた人もいるかもしれないけれど、２つの平行な直線に１つの直線が交わる時、

同位角は等しくなる（∠ａ＝∠ｅ、∠ｂ=∠ｆ、∠c＝∠ｇ、∠ｄ＝∠ｈ）
錯角は等しくなる（∠ｄ＝∠ｅ、∠ｃ＝∠ｆ）

という性質があるんだ。
この性質を使って角の大きさに関する問題にチャレンジしてみよう。

問題

上の２つの平行な直線に１つの直線が交わる時の図の中で、∠ａ・∠ｂと同じ大きさの角を全て答えなさい。

見た目で同じ大きさの角を見つけられる人もいると思うけれど、「なぜ同じ大きさになるか」ということも言えるようにしよう。

①∠ａと同じ大きさの角
２つの平行な直線に１つの直線が交わる時、同位角の角の大きさは等しいから∠ａ＝∠ｅ
対頂角の大きさは等しいから∠ａ＝∠ｄ
∠ｅと∠ｈは対頂角なので角の大きさは等しいから、∠ｅ＝∠ｈ
∠ａ＝∠ｅ、∠ｅ＝∠ｈより∠ａ＝∠ｈ

∠ａと同じ大きさの角は、∠ｄ、∠ｅ、∠ｈということがわかるね。

②∠ｂと同じ大きさの角
２つの平行な直線に１つの直線が交わる時、同位角の角の大きさは等しいから∠ｂ＝∠ｆ
対頂角の大きさは等しいから∠ｂ＝∠ｃ
∠ｆと∠ｇは対頂角なので角の大きさは等しいから、∠ｆ＝∠ｇ
∠ｂ＝∠ｆ、∠ｆ＝∠ｇより∠ｂ＝∠ｇ

∠ｂと同じ大きさの角は、∠ｃ、∠ｆ、∠ｇということがわかるね。

平行線になるための条件

実は平行線の性質の逆、つまり「同位角や錯角の大きさが等しければ、２つの直線は平行である」ということも正しいと言えるんだ。

定期テストでは、この性質を利用して平行な直線を見つける問題が出題されることもあるから確認しておこう。

例題

下の図の直線ａからｆの中で平行な組み合わせを答えなさい。

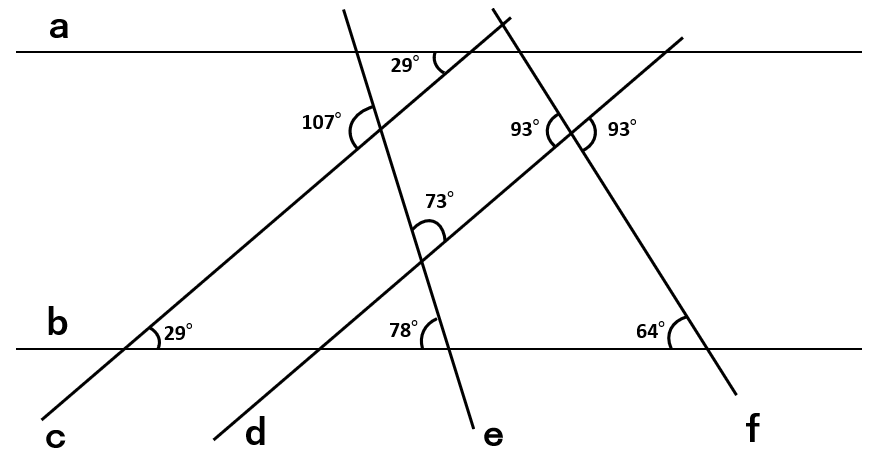
いくつもの直線が交わっていて、なかなか見つけるのに苦労しそうだよね。
平行の可能性がある２本の直線とそれらと交わる１本の直線の組み合わせを書き抜いて考えると、答えとなる組み合わせを見つけやすくなるよ。

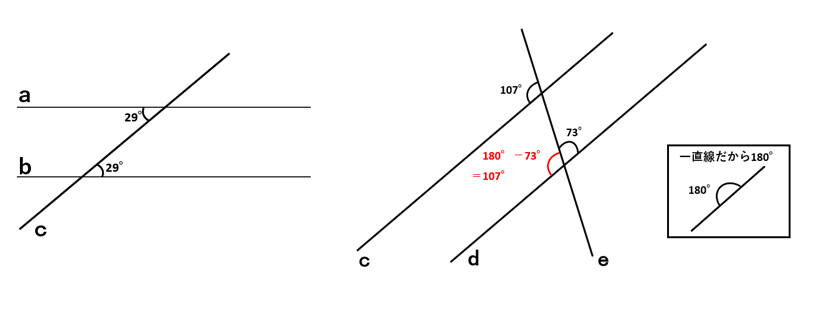
①直線ａ、直線ｂ、直線ｃの組み合わせ
直線ａと直線ｃで作られる２９°の大きさの角と直線ｂと直線ｃで作られる２９°の大きさの角の関係について考えよう。

この２つの角の位置関係は、「錯角」だね。
錯角の大きさが等しければ、２つの直線は平行である、という性質から直線ａと直線ｂは平行ということがわかるよ。

②直線ｃ、直線ｄ、直線ｅの組み合わせ
上の右側の図を見てみると、同じ大きさの角は問題の図にはないよね。
そこで１つ計算が必要になるんだ。

直線ｄと直線ｅから作られる７３°の隣の角の大きさを求めてみよう。
一直線が作る角は１８０°だから、１８０°ー７３°を計算して１０７°と求めることができるね。

直線ｃと直線ｅで作られる１０７°の大きさの角と直線ｄと直線ｅで作られる１０７°の大きさの角の関係は、同位角だね。

同位角の大きさが等しければ、２つの直線は平行である、という性質から直線ｃと直線ｄは平行ということがわかるよ。

今回の問題のように、角度を計算して求めるだけじゃなく、平行な直線を見つけるために角度に関する知識が必要な問題もあるから、色々な問題にチャレンジしてテストに備えよう！

対頂角・同位角・錯覚「平行線の性質」まとめ

対頂角・同位角・錯覚「平行線の性質」まとめ

２つの直線が交わった時に向かい合う角のことを対頂角と呼ぶ
対頂角の角の大きさは必ず等しくなる
２つの直線に１つの直線が交わって作られる角のうち、位置関係が同じ角を同位角と呼ぶ
２つの直線に１つの直線が交わって作られる角のうち、アルファベットのZと逆Zの形をしたところにできる位置関係の角を錯角と呼ぶ
２つの平行な直線に１つの直線が交わる時、同位角は等しくなる
２つの平行な直線に１つの直線が交わる時、錯角は等しくなる
同位角の大きさが等しければ、２つの直線は平行である
錯角の大きさが等しければ、２つの直線は平行である

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。