「多角形の内角の和」と「外角の和」の求め方をわかりやすく解説
中学2年生の数学で学習する「多角形の角」について、内角とはなにか、外角とはなにか、多角形の内角の和の求め方と、多角形の外角の和の求め方をわかりやすく解説するよ。
多角形の示し方
中学2年生の図形の単元がスタートするけれど、まずは中学1年生の時に習った内容の復習をしよう。
図形を示す時には、図形の名前の後に、頂点の名前(A、B、C、Dなど)を周にそって順に示すんだったんね。
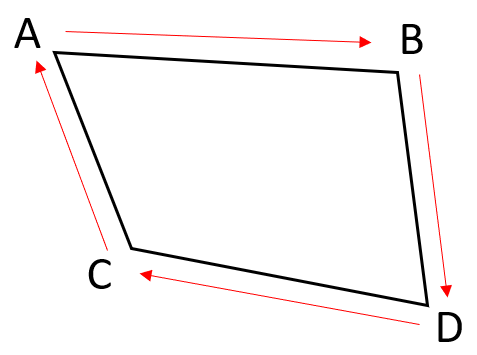
上の図であれば、図形は四角形で、頂点の順はA→B→D→Cだから、四角形ABDCとなるよ。
今回の図のように、頂点の順(上の図の場合:ABDC)=アルファベットの順(ABCD)にならない時もあるから注意しよう。
※上の図の四角形を書くときに、四角形ABCDと書いたら間違いになるよ。
多角形の外角とは
次は図形の角度の名前について確認しよう。
最初に確認するのは、外角という角なんだけれど、どんなものか図を使って説明するね。
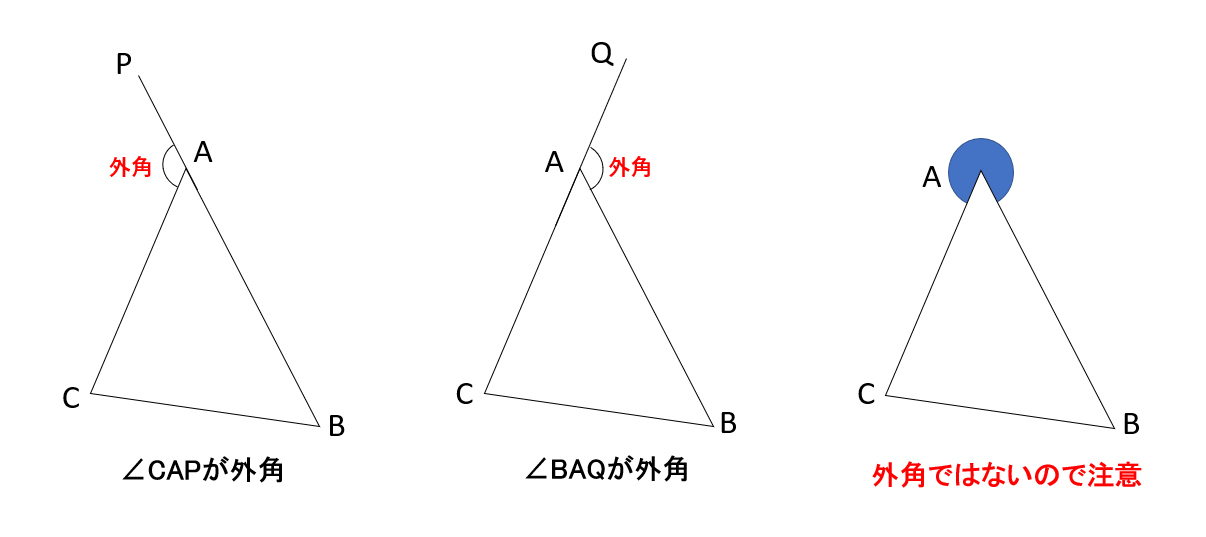
1つの辺と、その隣の辺を延長した時にできる図形の外側の角のことを外角というんだ。
頂点Aのところにできる外角は、上の図のように「辺ABを延長した場合の∠CAP」と「辺ACを延長した場合の∠BAQ」の2つのパターンが考えられるけれど、どちらでもOKだよ。
なぜなら、∠CAPの大きさと∠BAQの大きさは等しくなるからなんだ。
ちなみに3つ目に書いてある、「頂点Aの外側をぐるっと囲むような角」は、外角とは言わないので注意しよう。
※外角は180度よりも大きくなることはないので、覚えておこう!
多角形の内角とは
小学5年生の時に習った「内角」について、覚えているかな?
さっきの外角は図形の外側にできる角だけれど、内角は文字のとおり内側にできる角のことだったね。
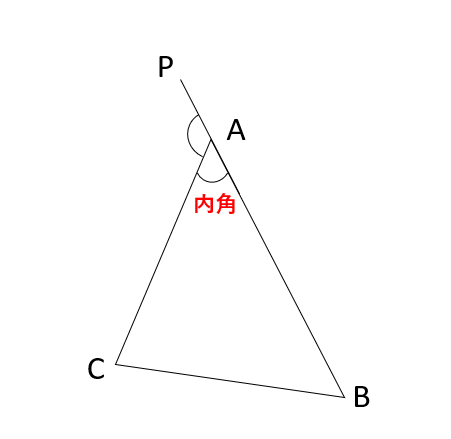
頂点Aのところにできている∠BAC(または∠CAB)が内角だね。
また上の図を見ると、1つの内角と隣り合う外角の和が180°になっていることに気づいたかな?
つまり∠BAC+∠CAP=180°という関係なっているんだ。
これは角度の計算問題でも使える便利な関係式だから、忘れずに覚えておこう!
多角形の内角の和
次は内角の和について確認していくよ。
三角形や四角形の内角の和は、それぞれ180°や360°になることは覚えているよね。
中学2年生で習う多角形では、八角形や十二角形などこれまで見たことがないような図形の内角の和を求める問題も出てくるんだ。
そこで、内角の和の求め方について確認をしていくよ。
多角形の内角の和は、「1つの頂点から対角線を引いたとき、いくつ三角形ができるか」という考え方を使って求めていくんだ。
四角形を例に見てみよう。
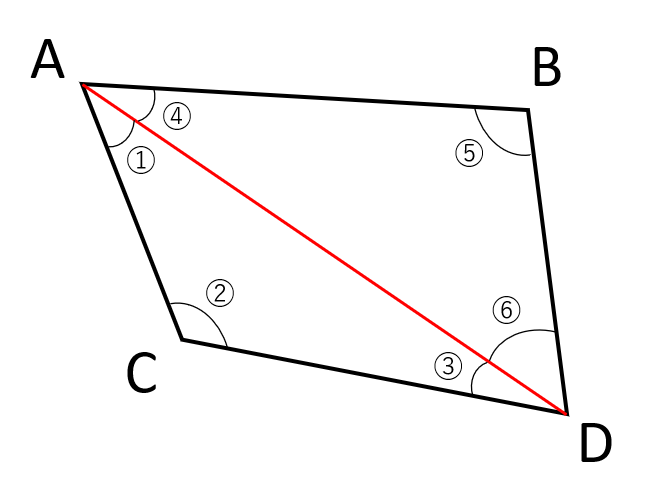
頂点Aから引くことができる対角線は1本(AD)だけだね。
対角線を引くと、四角形ABDCは△ACDと△ABDの2つに分けることができるね。
次に△ACDの①、②、③の角と△ABDの④、⑤、⑥の角の関係について見ていこう。
三角形の内角の和は180°になるから、
①+②+③=180°・・・・(1)
④+⑤+⑥=180°・・・・(2)
四角形ABDCの内角の和は、上の図で考えると
①+②+③+④+⑤+⑥となるから、(1)と(2)を足して360°と求めることができるんだ。
これを整理すると、
- 四角形では1つの頂点から対角線を引いて2つの三角形を作ることができる
- 四角形の内角の和は、三角形の数×2で求めることができる
ということがわかるよ。
実は四角形以外の五角形、六角形、七角形も同じように、1つの頂点から対角線を引いて作ることができる三角形の数を使って、内角の和を求めることができるんだ。
多角形ごとの三角形の個数と内角の和を求める式
| 四角形 | 五角形 | 六角形 | 七角形 | |
|---|---|---|---|---|
| 三角形の個数 | 2 | 3 | 4 | 5 |
| 内角の和を求める式 | 180×2 | 180×3 | 180×4 | 180×5 |
作ることができる三角形の個数は、その多角形の「辺の数-2」になっていることに気づいたかな?
※辺の数は、○角形の○の部分の数字と同じになるよ。四角形なら4本、五角形なら5本だね。
内角の和は、三角形の数、つまり「辺の数-2」に180を掛けると求めることができるよ。
この2つを組み合わせると、多角形の内角の和を求める公式は次のようになるよ。
多角形の内角の和を求める公式
(辺の数ー2)×180
早速この公式を使った練習問題にチャレンジしてみよう。
問題
十角形の内角の和を求めなさい。
この問題は、さっき習った公式をそのまま使えば、すぐに求めることができるね。
十角形だから、辺の数は10なので、(10-2)×180=1440と求めることができるよ。
公式を覚えていたら簡単に求めることができるから、公式を忘れないように色々な問題にチャレンジしよう。
多角形の外角の和
次は多角形の外角の和について確認をしよう。
内角のところで説明した「1つの内角と、隣り合う外角の和は180°」という性質を使って考えていくよ。
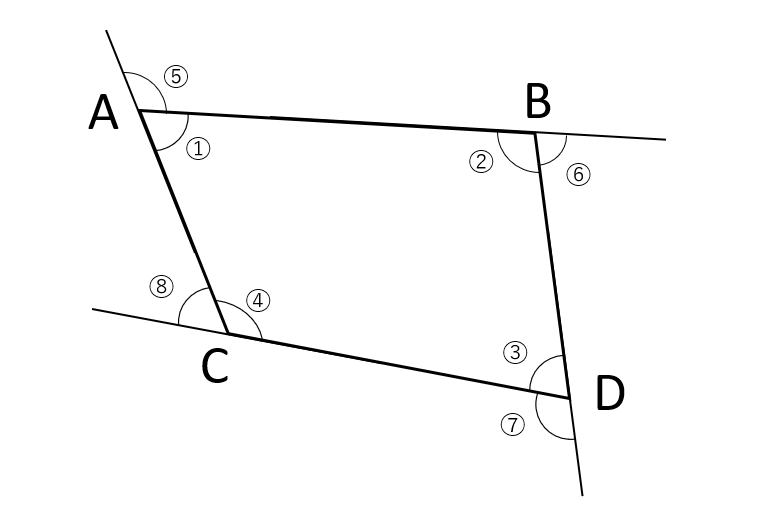
上の図で「1つの内角と、隣り合う外角の和は180°」だから
①+⑤=180°、②+⑥=180°、③+⑦=180°、④+⑧=180°
これを全て足すと
①+⑤+②+⑥+③+⑦+④+⑧=180°+180°+180°+180°
=720°・・・・(1)
四角形の内角の和は、360°だから
①+②+③+④=360°・・・・(2)
(1)の式を整理して、(2)を代入すると
①+②+③+④+⑤+⑥+⑦+⑧=720°
360°+⑤+⑥+⑦+⑧=720°
⑤+⑥+⑦+⑧=360°
⑤+⑥+⑦+⑧は四角形の外角を足したものだから、四角形の外角の和は360°になるということがわかるんだ。
つまりは、まず全ての「内角+外角」の合計である720°を求めて、そこから「内角の合計の360°」を引けば、「残りは外角の合計」になるという考え方だね。
他の多角形でも同じように計算すると、外角の和を求めることができるんだけれど、実はどの多角形も外角の和は360°になるんだ。
だから、外角の和を聞かれたときには計算不要で360°と答えよう。
非常にシンプルな性質なんだけれど、色々な問題で使われる考え方だから、問題演習を通して使い方をマスターしよう。
問題
(1)正十二角形の外角の和を求めなさい
(2)正十二角形の1つの外角の大きさを求めなさい。
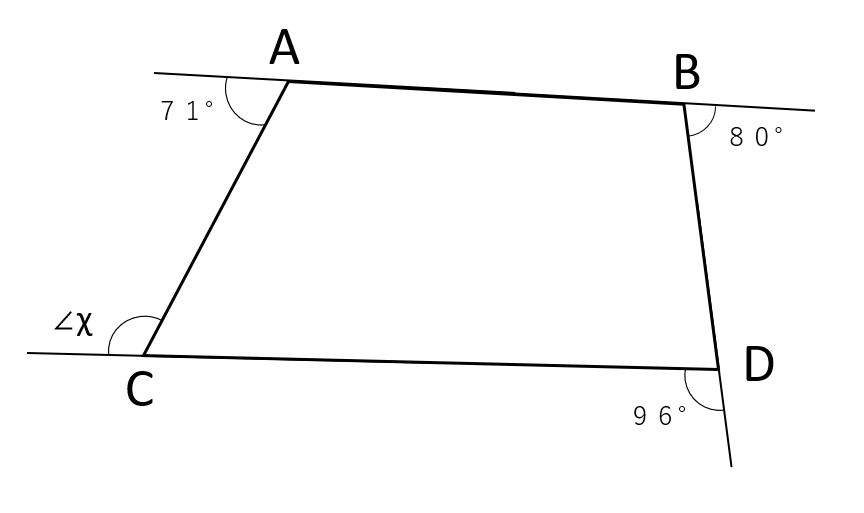
(3)下の図の∠χの大きさを求めなさい。
(1)正十二角形の外角の和
何角形でも、外角の和は必ず360°になるから、答えは360°になるよ。
(2)正十二角形の1つの外角の大きさ
正十二角形の外角の和が360°だから、それを12等分すればOKだよ。
360°÷12=30°
(3)∠χの大きさ
「多角形の外角の和は360°」の性質を使うと求めることができる問題だね。
∠χ以外の外角がわかっているので、360°から∠χ以外の角度の合計を引いてあげれば、∠χの角度を求めることができるね。
71°+80°+96°+χ=360°
χ=360°-247°
χ=113°
「内角の和の公式」や「多角形の外角の和は360°」の考え方を使った問題は定期テストでよく出題されるから、学校のワークや教科書の問題で繰り返し練習をしよう!
「多角形の内角の和・多角形の外角の和」まとめ
「多角形の内角の和・多角形の外角の和」まとめ」
- 図形を示す時には、図形の名前の後に、頂点の名前(A、B、C、Dなど)を周にそって順に示す
例:四角形ABDC(※アルファベット順とはかぎらないので注意しよう) - 1つの辺と、その隣の辺を延長した時にできる図形の外側の角のことを外角という
※外角は180度よりも大きくなることはない - 図形の内側にできる角のことを「内角」という
- 「1つの内角と、隣り合う外角の和は180°」になる
- 多角形の内角の和は、(辺の数ー2)×180で求めることができる
※辺の数は、〇角形の「〇」の数と等しい - どの多角形も外角の和は360°になる
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。