「三角形の合同条件3つ」とは?なぜ合同になるのか?くわしく解説
中学2年生の数学で学習する「三角形の合同条件」について、三角形の合同条件3つをそれぞれくわしく紹介。なぜそれらが合同の条件となるのか、実際に作図をしてみながら、基本から解説していくよ。
合同な三角形をかくのに必要な条件とは
2つの図形がぴったり重なり合うとき、2つの図形は「合同」というんだったね。
それでは、「合同な図形」をかくには、どんな方法があるんだろう?
今回の学習では、「合同な2つの三角形」をかくにはどうすればいいのか、「2つの三角形が合同である」ということを証明するには、どんな条件がそろえばいいのか?を考えていくよ。
それでは、まず「合同な三角形をかく方法」について確認していこう。
これまでに解いたことがある作図の問題と同じように、「辺の長さ」と「角の大きさ」に注目して、どんな条件の時に決まった1つの三角形を作図できるかを考えてみよう。
ある条件のときに、「決まった1つの三角形を作図できる」ということは、つまり「その条件だと、かならず決まった形の三角形になる」ということだよね。
かならず決まった形の三角形になるということは、その条件でかいた三角形は、すべておなじ形になるから、「合同になる」ということなんだよ。
だから、その「条件」がなにかを探そう、ということだね。
その条件は、3つあるんだよ。
①3つの辺の長さがわかっている時
3つの辺の長さが、3cm、7cm、8cmの三角形の作図をすると考えてみよう。
3つの辺のうち、どれか1つの辺を定規を使ってひき、残りの2辺の長さをコンパスで取り、作図をすると1つの三角形しかできないよ。
※回転したものは同じ三角形として考えるよ。
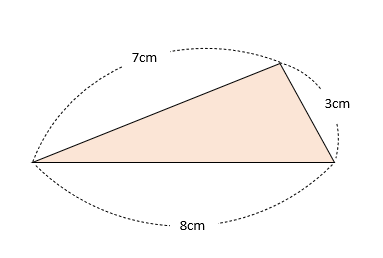
3つの辺の長さがわかるだけで、かならずひとつの決まった三角形になるなんて、すこし不思議だよね。
でも、実際に3つの長さが決まった辺を、スキマや余分な辺ができないようにして三角形をつくろうとしてみると、「ぴったり3つの辺が組み合わさって三角形になる」形は、たった一つしかないことがわかるよ。
合同な三角形をかくための条件➀
3つの辺の長さが決まると、たったひとつの三角形にしかならない
→「3つの辺の長さが同じであれば、合同の三角形になる」
②2つの辺の長さと2辺の間の角の大きさがわかっている時
まずは、「2つの辺の長さと1つの角の大きさがわかっている」場合の作図について考えてみるよ。
たとえば、2つの辺の長さが4cmと8cmで、1つの角の大きさが30°の三角形の作図をするとしたらどうなるだろう。
2つの辺のどちらか1つの辺を定規を使ってひき、角度は分度器を使い、残りの1辺はコンパスを使って作図をしてみよう。
たとえば、8cmの辺を定規を使ってひいて、その8cmの辺の右端に分度器で30°を測って、残りの1辺(4cm)はコンパスを使って作図するとするよ。
この方法で三角形を作図すると、2通りの三角形がかけてしまうんだ。
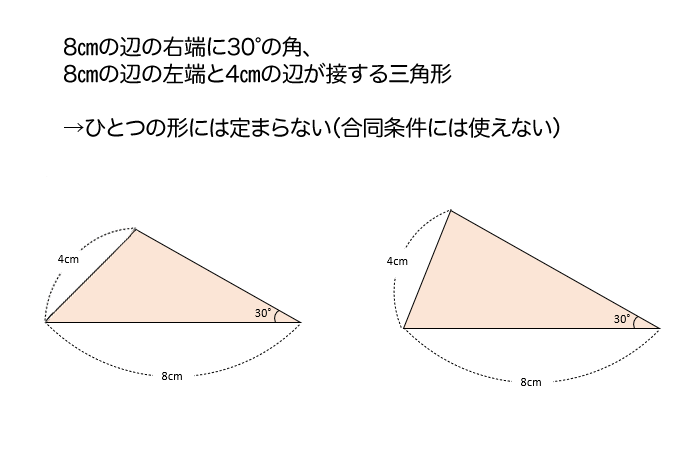
どうしてかというと、
角30°を作る直線と、8cmの辺の左端を中心とした半径4cmの円の交わる点は、2つあるから。
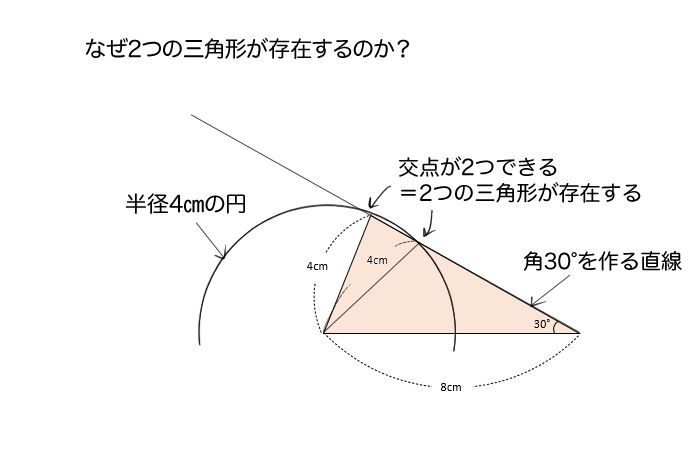
ということは、2辺と1つの角がわかっただけでは、三角形の形は何通りかできてしまうので、ひとつに定まらないね。
だから、合同条件にすることはできないね。
でも、「1つの角の位置」を長さがわかっている『2辺の間の角』とすると、なんと作図結果は1つになるんだ。
「8cmの辺と、4cmの辺の間が、30°の角」の三角形を作図してみよう。
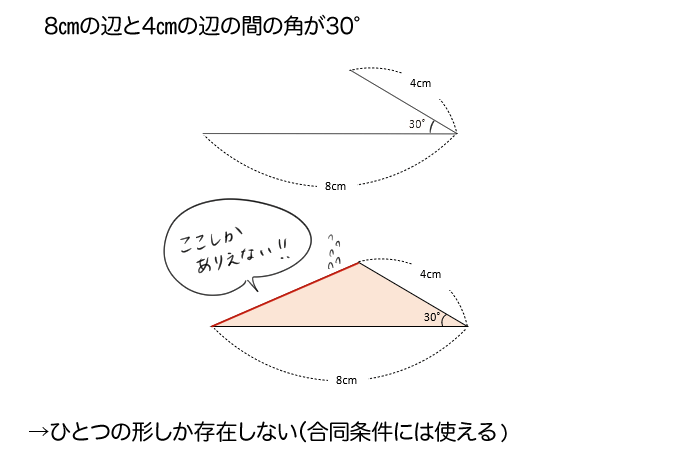
2つの辺と、その間の角の大きさがわかれば、できる三角形はたった一つになるよ。
ということは、「2つの辺と、その間の角が同じ三角形は、合同になる」といえるね。
合同な三角形をかくための条件➁
2つの辺の長さと、その間の角の大きさが決まると、たったひとつの三角形にしかならない
→「2つの辺の長さとその間の角が同じであれば、合同の三角形になる」
③1つの辺の長さと2つの角の大きさがわかっている時
それでは、「1つの辺の長さと、2つの角の大きさがわかっている」場合はどうだろう?
たとえば、1つ辺の長さが4cmで、2つの角の大きさが30°と45°の三角形の作図をして考えてみよう。
1つの辺は定規を使ってひき、角度は分度器を使って作図をしてみよう。
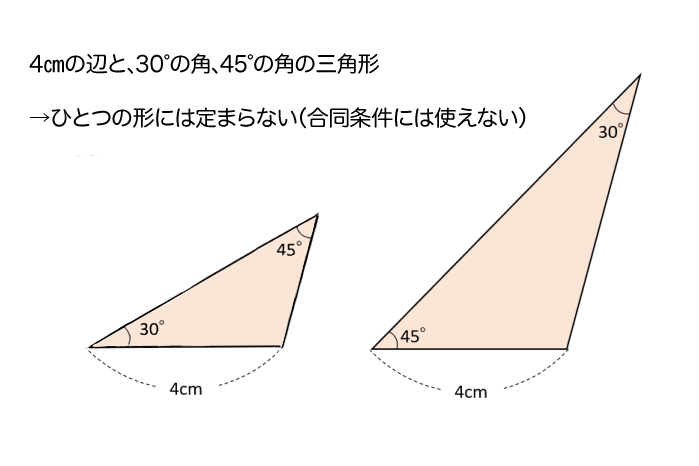
このパターンも上の図のように、4cmの辺の左端に30°の角があるのか、それとも45°の角があるのかによって2通りの作図結果ができてしまうんだ。
ということは、1つの辺の長さと、2つの角の大きさがわかっただけでは、三角形の形は1つには定まらないので、合同条件に使うことはできないね。
けれど、「2つの角の位置」を長さがわかっている『1辺の両端』とすると作図結果は1つになるんだよ。
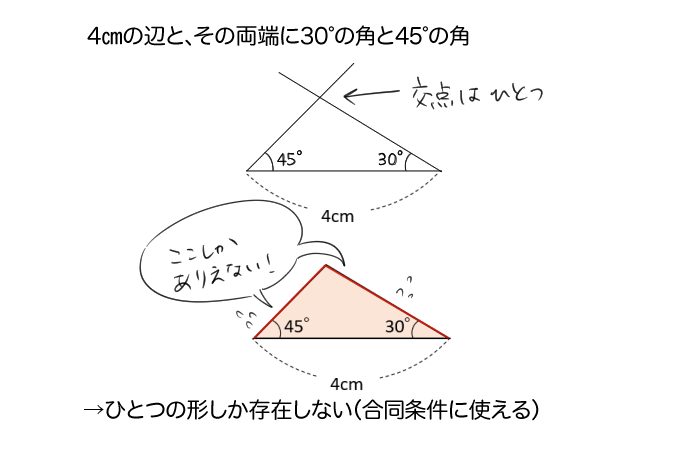
1つの辺と、その両端の角の大きさがわかれば、できる三角形はたった一つになるんだね。
ということは、「1つの辺と、その両端の角が同じ三角形は、合同になる」といえるね。
合同な三角形をかくための条件③
1つの辺の長さと、その両端の角の大きさが決まると、たったひとつの三角形にしかならない
→「1つの辺の長さとその両端の角が同じであれば、合同の三角形になる」
この3つのパターンをまとめると
- 3つの辺の長さがわかっている時
- 2つの辺の長さとその間の角の大きさがわかっている時
- 1つの辺の長さとその両端の角の大きさがわかっている時
この3つのうち、いずれかの条件の時は、合同な三角形を作図することができるということだね。
三角形の合同条件
合同な三角形をかくのに必要な条件がわかったとおり、次の3つの条件のどれかが当てはまれば、2つの三角形がぴったり重なるかどうかを確認しなくても、「合同であると判断する」ことができるよ。
この、「2つの三角形が合同であると判断することができる条件」を、「三角形の合同条件」と呼ぶんだ。
三角形の合同条件
①3組の辺がそれぞれ等しい。
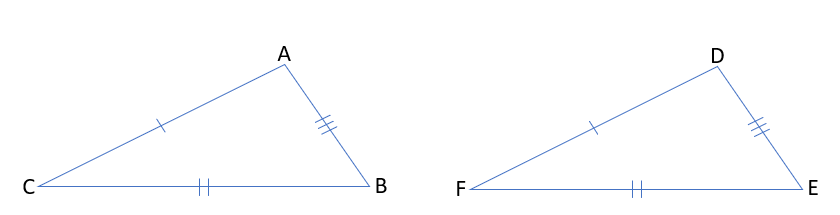
AB=DE、BC=EF、CA=FD
②2組の辺とその間の角がそれぞれ等しい。
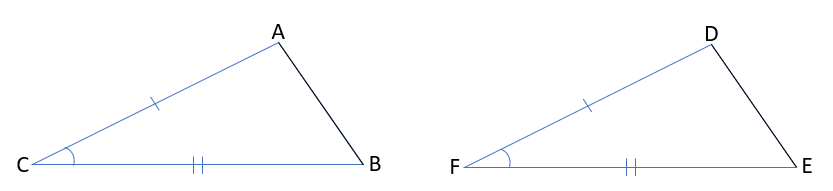
BC=EF、CA=FD、∠ACB=∠DFE
③1組の辺とその両端の角がそれぞれ等しい。
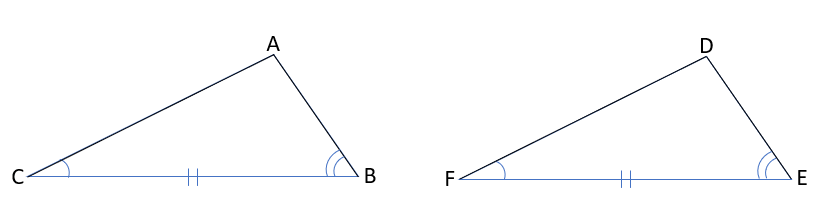
BC=EF、∠ACB=DFE、∠ABC=∠DEF
三角形の合同条件については、教科書や参考書によって表現(使う言葉など)が異なる場合があるから、学校で習った表現で覚えるようにしよう。
ところで、「3つの角が等しい場合」は、合同にならないの?
と思った人がいるかもしれないね。
3つの角度が等しいだけでは、辺の長さが違う「拡大・縮小した関係」の三角形が作図できる場合があるので、「合同」にはならないから注意しよう。
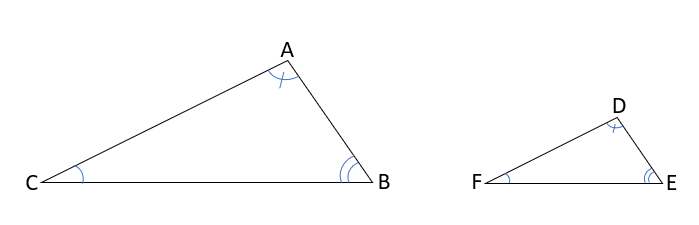
ちなみに、このように「2つの図形が拡大縮小の関係になっている」ときは、合同ではなく『相似』と呼ぶんだ。
詳しくは中学3年生で習うから楽しみにしていてね!
「三角形の合同条件」まとめ
三角形の合同条件まとめ
- 「2つの三角形が合同であると判断することができる条件」を、「三角形の合同条件」と呼ぶ
- 三角形の合同条件3つ
3組の辺がそれぞれ等しい
2組の辺とその間の角がそれぞれ等しい
1組の辺とその両端の角がそれぞれ等しい - 「3つの角が等しい」三角形は、合同であるとはいえないので注意する
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。



