「確率の求め方」確率pとは?公式と練習問題をわかりやすく解説
中学2年生の数学で学習する「確率」について、「同様に確からしい」とはどういうことか、「確率p」とは何か、確率の求め方と公式をわかりやすく解説するよ。
練習問題をもとに、確率の問題の解き方もくわしく紹介。
「確率」とは
「確率」ということばは、日常でもよく使うよね。
「こんなことが起こるなんて、すごい確率だ!!」とか、「高確率で当たる!!」とか。
「すごい確率だ!」と驚くときは、「めったに起こらないことが起きてびっくりだ!」ということだし、「高確率で当たる!」というのは、「ほとんどの場合当たるよ!」ということだよね。
「確率」とは、「ある事が、どのくらい起こりやすいか」を表すものなんだ。
「同様に確からしい」とは
確率は、ある事がどのくらい起こりやすいかを表すことばだけれど、世の中には、「起こりやすさが平等」なものもあるんだ。
たとえば、100円玉1枚を100回投げた時に、表(おもて)が何回出るか考えてみよう。
100回投げるあいだ、「表・裏」と交互に出る時もあれば、「表・表」や「裏・裏」のように、同じものが連続する時もあるよね。
ただ、最終的に100回投げ終わるときには、表が出た回数は50回、裏が出た回数も50回、のように表が出る数と裏が出る数は「同じ回数ぐらい」になるんだ。
このように、表や裏のどちらかが多く出ずに、どちらの側も同じ程度出る場合のように、起こりやすさが平等なことを同様に確からしいというんだ。
ちなみに100回投げただけでは、実際には「表が48回で、裏は52回」などのようにすこし偏ったりすることもあるんだけれど、これを1000回、10000回と投げる回数を増やせば増やすほど、表の数と裏の数は、ほぼ同じ回数になるよ。
これは、回数が多くなればなるほど、あることが起きる頻度は、精度が増して確率どおりに起こるようになるからだよ。
「さいころの出る目の数」についても同じように見てみよう。
さいころを投げた時に「1の目が出た回数」を集計すると、下の表のようになったよ。
| 投げた回数 | 1の目が出た回数 |
|---|---|
| 60回 | 14回 |
| 600回 | 110回 |
| 6000回 | 1072回 |
| 60000回 | 10033回 |
さいころを投げた回数が増えるほど、「1の目が出た回数」は、「さいころを投げた回数」を6で割った数に近づいていくことがわかるね。
上の表は「1の目が出た回数」だけを数えているけれど、他の「2」・「3」・「4」・「5」・「6」の目も、60000回さいころを投げた時には、約10000回出たよ。
つまり、さいころを投げたときにどの目が出るかも、「起こりやすさが平等」なんだね。
確率の求め方
確率とは、「ある事がどのくらい起こりやすいか」を表すことばだったね。
でも、どのくらい起こりやすいかを「あんまり起こらない」とか、「よく起こる」なんてざっくりしか表せないと、困ることもあるよね。
そこで、「ある事がどのくらい起こりやすいか」を数字で表すにはどうすればいいのかを考えてみよう。
さいころのそれぞれの目の出る確率を考えてみよう
「さいころの目の出る数」を集計したときは、さいころを60000回投げた時、「1・2・3・4・5・6」の6つの目それぞれの出た回数は、どれも「約10000回」になったんだったよね。
60000回のうち10000回出たということは、つまり投げた回数の\(\frac{1}{6}\)回ということだね。
なぜ\(\frac{1}{6}\)になるのかというと、「さいころを投げたときにどの目が出るか」は、「起こりやすさが平等」なのだから、「1・2・3・4・5・6」の6つの目で平等にするから\(\frac{1}{6}\)になるんだよ。
このように、確率は「\(\frac{ある事が起こりうる場合の数}{起こりうる場合の数}\)」で求めることができるんだ。
※起こりうる場合の数=「1・2・3・4・5・6」の6つの目があるので、6通り。
※ある事が起こりうる場合の数=それぞれの目が出る場合は1通り。
確率の公式
確率の求め方
起こりうる場合が全部でn通りあり、Aの起こる場合がa通りあるとき、Aの起こる確率pは、次のように求めることができる。
p=\(\frac{n}{a}\)
「確率p」の「p」は、英語で「確率」という意味の「probability」の頭文字だよ。
ちなみに、確率pの値は、必ず0≦p≦1の範囲になるから、計算結果が1よりも大きい値が出た場合には、式や計算間違いということがわかるよ。
決して起こらないことがらの確率が「0」になるのは分かりやすいよね。
どうして必ず起こることがらの確率が「1」になるのかというと、確率は\(\frac{ある事が起こりうる場合の数}{起こりうる場合の数}\)だということを考えてみて。
必ず起こるということは、この分母と分子が同じ数になるんだ。
さいころで言えば、「6回中6回出る」という状態。
だから、\(\frac{6}{6}\)=1になるんだよ。
さいころの偶数の目がでる確率を考えてみよう
さいころのそれぞれの目が出る確率は\(\frac{1}{6}\)だね。
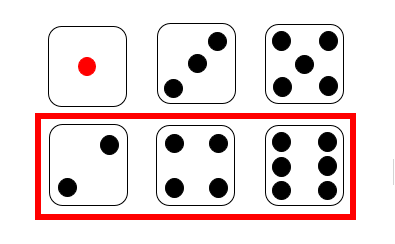
では、さいころを1つ投げた時に「偶数の目が出る確率」を求めてみよう。
さいころの目の出方は全部で6通りあって、どの目が出ることも同様に確からしい(平等にどの目も出る)から、偶数の目が出る場合は「2・4・6」が出る「3通り」だよね。
この時の確率は、「\(\frac{ある事が起こりうる場合の数}{起こりうる場合の数}\)」に当てはめると、\(\frac{偶数の目が出る場合の数}{全部の目が出る場合の数}\)となるよ。
さいころを1つ投げた時に偶数の目が出る確率=\(\frac{3}{6}\)=\(\frac{1}{2}\)
この答えから6回中3回、つまり、2回に1回は偶数の目が出る可能性がある、ということがわかるんだ。
確率を求める問題
それでは、確率を求める練習問題に挑戦してみよう。
問題
ジョーカーを除く52枚のトランプから1枚ひくとき、次の確率を求めなさい。
(1)ひいたカードが、エースである確率
(2)ひいたカードが、ハートである確率
(3)ひいたカードが、ジョーカーである確率
(1)
起こりうる場合は、全部で52通りだね。
エースは、ハート・ダイヤ・クラブ・スペードで1枚ずつあるから、エースを引くのは、全部で4通りあるね。
だから求める確率は、
\(\frac{4}{52}\)=\(\frac{1}{13}\)
と求めることができるよ。
(エースは、13回に1回は引くことができるということだよ。)
(2)
起こりうる場合は、全部で52通りだね。
ハートは全部で13枚あるから、ハートを引くのは全部で13通りだよ。
だから求める確率は、
\(\frac{13}{52}\)=\(\frac{1}{4}\)
と求めることができるよ。
(ハートは、4回に1回は引くことができるということだよ。)
(3)
起こりうる場合は、全部で52通りだね。
ジョーカーは、このトランプには含まれていないから、ジョーカーを引く場合の数は、0だよ。
だから求める確率は、
\(\frac{0}{52}\)=0
と求めることができるよ。
(ジョーカーは、絶対に引くことができないということだよ。)
確率の計算では、約分をすることが多くなるから、約分のし忘れや計算間違いに注意しよう。
確率まとめ
起こりうる場合が全部でn通りあり、Aの起こる場合がa通りあるとき、Aの起こる確率pは、次のように求めることができる。
p=\(\frac{n}{a}\)
確率pの値は、必ず0≦p≦1の範囲になり、必ず起こることがらの確率は1、決して起こらないことがらの確率は0となる。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。


