「一次関数の式の求め方」をパターン別にわかりやすく解説
中学2年生の数学で学習する一次関数について、グラフから一次関数の式を求める方法や、「傾き」「切片」「座標」それぞれのうちどれが分かっているかによるパターンごとの式の求め方をくわしく解説するよ。
これまでの学習で「一次関数のグラフの特徴」や、一次関数の「傾き」や「切片」「座標」について学習してきたね。
今回は、一次関数の式を、グラフを読み取って求める方法や、分かっている「傾き」「切片」「座標」の乗法などから求める方法を学習するよ。
「グラフ」、「傾き」、「切片」、「座標」のうち何が分かっているかによって、式を求める方法が変わるんだ。
何が読み取れるかのパターン別に、式を求める方法をそれぞれ解説していくよ。
一次関数の式の求め方
「グラフ」から式を求めてみよう
まずは、「一次関数のグラフ」から式を求める方法を確認しよう。
グラフから一次関数の式を求める手順
①切片を確認して、y=aχ+bのbを求める
②χのプラス側で読み取りやすい点を見つける
③切片から②の点まで「右にいくつ進んだか」「上下にいくつ進んだか」を求める
④③で求めた値をa=\(\frac{上下に進んだ数}{右に進んだ数}\)に代入してaを求める
上の手順で早速グラフから一次関数の式を求めてみよう。
問題
(1)(2)のグラフから一次関数の式を求めなさい。
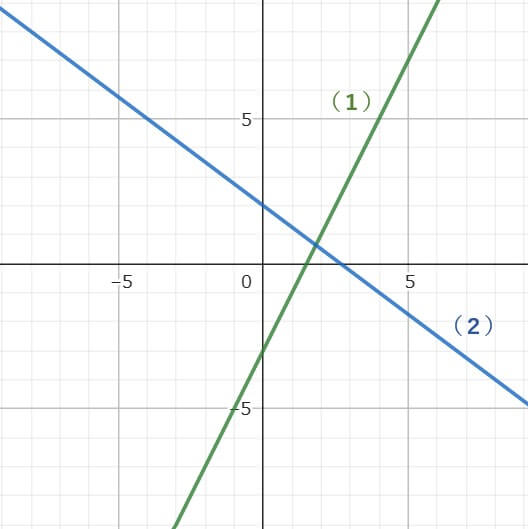
(1)
確認した手順の通りに問題を解いていこう。
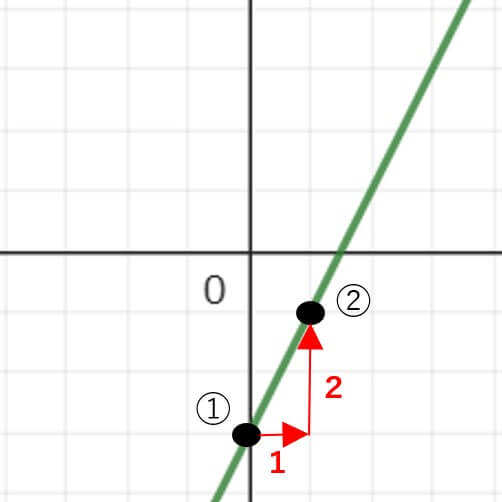
①切片を確認して、y=aχ+bのbを求める
切片の座標は上のグラフから(0、-3)だね。
だからbは-3ということがわかるよ。
②χのプラス側で読み取りやすい点を見つける
上のグラフの②の点(1、-1)が読み取りやすい点だね。
※(2、1)や(3、3)を読み取った場合でも式を求めることができるよ。
③切片から②の点まで「右にいくつ進んだか」「上下にいくつ進んだか」を求める
上のグラフから、切片から②の点は、「右に1」「上に2」進んでいることがわかるね。
④③で求めた値をa=\(\frac{上下に進んだ数}{右に進んだ数}\)に代入してaを求める
a=\(\frac{上下に進んだ数}{右に進んだ数}\)に③で求めた「右に1」「上に2」を代入するよ。
a=\(\frac{2}{1}\)
=2
これで、(1)の式がy=2χ-3と求めることができたね!
※ちなみに、②で(2、1)を読み取った場合、切片から「右に2」「上に4」進むから、a=\(\frac{上下に進んだ数}{右に進んだ数}\)に代入すると
a=\(\frac{4}{2}\)
=2
となって、aの値は同じさっき求めたものと同じになるよ。
同じ手順で(2)も求めてみよう。
(2)
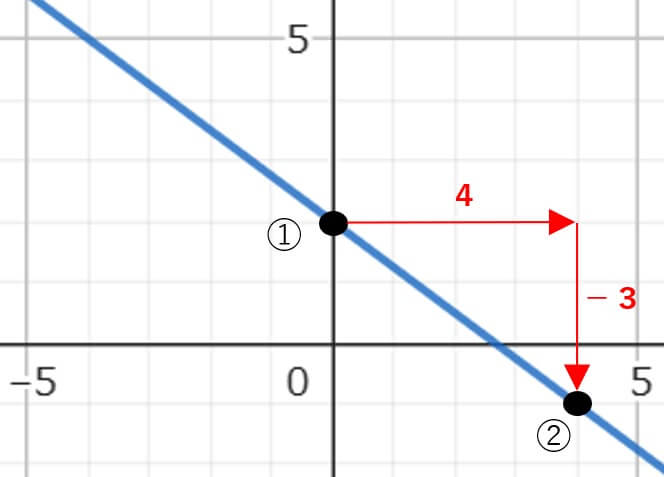
①切片を確認して、y=aχ+bのbを求める
切片の座標は上のグラフから(0、2)だね。
だからbは2ということがわかるよ。
②χのプラス側で読み取りやすい点を見つける
上のグラフの②の点(4、-1)が読み取りやすい点だね。
③切片から②の点まで「右にいくつ進んだか」「上下にいくつ進んだか」を求める
上のグラフから、切片から②の点は、「右に4」「下に3」進んでいることがわかるね。
④③で求めた値をa=\(\frac{上下に進んだ数}{右に進んだ数}\)に代入してaを求める
a=\(\frac{上下に進んだ数}{右に進んだ数}\)に③で求めた「右に4」「下に3」を代入するよ。
※「下に3」ということは、-3を代入するよ。
a=\(\frac{-3}{4}\)
=-\(\frac{3}{4}\)
これで、(2)の式がy=-\(\frac{3}{4}\)χ+2と求めることができたね!
グラフから式を求める時は、難しい計算もないから、手順を覚えるまで何度も繰り返しも問題に取り組もう。
一次関数の式の求め方
「傾きと切片が分かっている」場合
では、「傾き」と「切片」が分かっている場合の一次関数の式の求め方はどうすればいいのだろう?
y=aχ+bの基本知識も確認することも含めて、傾きと切片がわかっている場合の一次関数の式を求めてみよう。
y=aχ+bのa、bにはそれぞれ名前があったのは覚えているかな?
aは、「傾き」「比例定数」「変化の割合」
bは、「切片」
これがわかっていれば、これから取り組む問題は簡単に解くことができるよ。
問題
次の一次関数の式を求めなさい。
(1)傾きが-5、切片が-2
(2)傾きが3、切片が-1
(1)(2)のどちらもaが傾き、bが切片ということがわかればすぐに求めることができるね。
(1)
傾きが-5だから、aが-5
切片が-2だから、bが-2
一次関数の式は、y=-5χ-2
(2)
傾きが3だから、aが3
切片が-1だから、bが-1
一次関数の式は、y=3χ-1
aが傾き、bが切片という知識は、一次関数では非常に重要な知識だから忘れることが無いようにしっかり確認しておこう。
一次関数の式の求め方
「傾きと通る1点の座標が分かっている」場合
次に「傾き」だけがわかっているパターンの問題にチャレンジしてみよう。
ここからはいよいよ計算が必要になるけれど、決して難しい計算ではないから、丁寧にミスなく取り組んでいこうね。
まずは、例題を使って解き方を確認していくよ。
例題
yがχの一次関数で、そのグラフの傾きが3で、点(-2、1)を通るとき、この一次関数の式を求めなさい。
問題文から「傾きが3」ということは、a=3ということだからy=3χ+bとなるね。
次に点(-2、1)を通る、と書いてあるね。
これは、これから求める式は、χ=-2のときy=1ということを表してるから、y=3χ+bに代入しよう。
1=3×(-2)+b
1=-6+b
b=-7
と求めることができたね。
つまり、この式の切片は-7ということがわかったね。
これで、傾きが3、切片が-7とわかったので、この問題の答えは
y=3χ-7となるよ。
傾きと通る1点の座標がわかっているときの一次関数の式を求める手順
①傾きを代入して、y=○χ+bの形にする。
※○には数字が入るよ。
②通る1点の座標を式に代入して、bを求める。
手順はこれだけだから、計算ミスしないように解くことができれば問題なし!
早速問題にチャレンジしてみよう。
問題
次の条件を満たす一次関数の式を求めなさい。
(1)傾きが-2で、点(3、2)を通る。
(2)傾きが\(\frac{3}{2}\)で、点(4、-1)を通る。
それでは、さっき確認した手順通りに問題を解いていこう。
(1)
①傾きを代入して、y=○χ+bの形にする。
傾きが-2だから、y=-2χ+bとなるね。
②通る1点の座標を式に代入して、bを求める。
通る点は(3、2)だから、χ=3のときy=2ということだね。
これを①の式に代入すると
2=-2×3+b
2=-6+b
b=8
となるから、求める式はy=-2χ+8ということがわかるよ。
(2)
①傾きを代入して、y=○χ+bの形にする。
傾きが\(\frac{3}{2}\)だから、y=\(\frac{3}{2}\)χ+bとなるね。
②通る1点の座標を式に代入して、bを求める。
通る点は(4、-1)だから、χ=4のときy=-1ということだね。
これを①の式に代入すると
-1=\(\frac{3}{2}\)×4+b
2=6+b
b=-4
となるから、求める式はy=\(\frac{3}{2}\)χ-4ということがわかるよ。
傾きを式に当てはめて点を代入する、というシンプルな手順だからミスなく取り組んでいこう。
一次関数の式の求め方
「通る2点の座標が分かっている」場合
一次関数の式を求める最後のパターンにチャレンジしよう。
傾きも切片もわからず、「通る2点の座標だけがわかっている問題」なんだ。
例題を使って解き方を確認していくよ。
例題
yがχの一次関数で、そのグラフが2点(-2、1)、(3、6)を通るとき、この一次関数の式を求めなさい。
実はこの問題は2つの求め方があるんだ。
それぞれの解き方について確認していくよ。
パターン1 連立方程式を使った解き方
まずは、y=aχ+bにそれぞれの点を代入すると
1=-2a+b
6= 3a+b
この2つの式を連立方程式として計算して、aとbを求めよう。
実はこの計算は、bの係数が絶対に1になるから、2つの式をひき算すればOKだよ!
1=-2a+b
-)6= 3a+b
↓ ひき算をたし算に変えて(符号を変えるのも忘れずに)
1=-2a+b
+)-6=-3a-b
-5=-5a
a=1
↓ これを1=-2a+bに代入すると
1=-2×1+b
1=-2+b
b=3
計算結果からy=χ+3と求めることができたね!
この方法は、解く手順はシンプルだけれど、計算ミスしないように注意が必要だよ。
パターン2 傾きを使った解き方
次の解き方は、2点から傾きを求める方法だよ。
解く手順は少し多くなるけれど、計算量が少ないから、計算に自信がない人にはおすすめだよ。
①「右に進んだ数」と「上下に進んだ数」から、傾きを求める
与えられた2点をグラフに描いて、「右に進んだ数」と「上下に進んだ数」を求めるところからスタートするよ。
※慣れたらグラフは省略してもOKだよ。
慣れるまでは途中式と同じように書き残しておくと、ミスなく解くことができるよ。
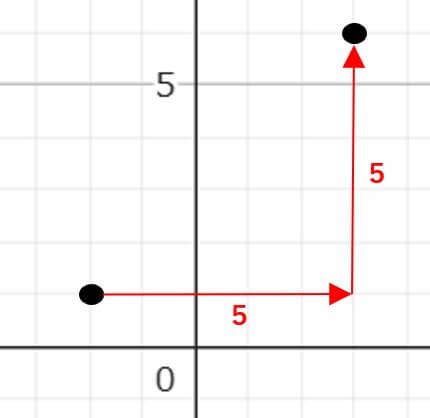
グラフはこんな感じでOKだよ。
これを見てみると、(-2、1)から(3、6)までは
右に5進んで、上に5進んだ点、ということがわかるね。
これをa=\(\frac{上下に進んだ数}{右に進んだ数}\)に代入すれば、傾きを求めることができるよ。
a=\(\frac{5}{5}\)
=1
これで傾きを求めることができたね!
※一番最初のグラフから一次関数の式を求める問題では、切片をスタートの位置にしていたけれど、切片がわからない場合には、今回の問題のように切片以外の点をスタート位置にしてもOKだよ。
②2点のうち好きな方の座標を式に代入して、bを求める。
①からy=χ+bまでは求められたから、この式に2点(-2、1)、(3、6)のどちらかを代入して、bを求めよう。
今回は(-2、1)を代入するね。
1=1×(-2)+b
1=-2+b
b=3
この結果から、今回求める式はy=χ+3と求めることができて、パターン1で解いた答えと同じ答えになったね。
通る2点がわかっている一次関数の式の求め方
パターン1 連立方程式を使った解き方
2点をy=aχ+bに代入して、出てきた2つの式を連立方程式として計算する。
パターン2 傾きを使った解き方
①「右に進んだ数」と「上下に進んだ数」から、傾きを求める
②2点のうち好きな方の座標を式に代入して、bを求める。
確実にミスなく解くことができるパターンを使っていこう!
問題
次の条件を満たす一次関数の式を求めなさい。
(1)グラフが2点(-1、7)、(1、3)を通る。
(2)χ=2のときy=-3、χ=4のときy=-9
(1)
この問題は連立方程式を使った解き方で解説するよ。
傾きを使った解き方をした場合は、求めた式が一致するか確認しよう。
また、余裕がある場合には連立方程式を使った解き方にもチャレンジしてみよう。
2点をy=aχ+bに代入すると
7=-a+b
3= a+b
これを連立方程式として、計算すると
(今回はたし算をすると簡単に計算できるよ!)
7=-a+b
+)3= a+b
10= 2b
b=5
これを7=-a+bに代入すると
7=-a+5
2=-a
a=-2
計算結果から答えは、y=-2χ+5となるね。
(2)
この問題は、傾きを使った解き方で解説するよ。
連立方程式を使った解き方をした場合は、求めた式が一致するか確認しよう。
また、余裕がある場合には傾きを使った解き方にもチャレンジしてみよう。
①「右に進んだ数」と「上下に進んだ数」から、傾きを求める
与えられた2点をグラフに描いて、「右に進んだ数」と「上下に進んだ数」を求めよう。
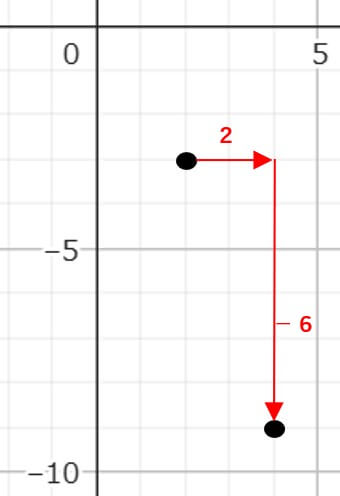
これを見てみると、「χ=2のときy=-3」から「χ=4のときy=-9」までは
右に2進んで、下に6進んだ点、ということがわかるね。
これをa=\(\frac{上下に進んだ数}{右に進んだ数}\)に代入すると
a=\(\frac{-6}{2}\)
=-3
これで傾きが-3とわかったね。
②2点のうち好きな方の座標を式に代入して、bを求める。
①からy=-3χ+bまでは求められたから、この式にχ=2、y=-3を代入して、bを求めよう。
※χ=4、y=-9を代入しても同じ答えになるよ。
-3=-3×2+b
-3=-6+b
b=3
これで答えは、y=-3χ+3ということがわかったね。
一次関数の式を求める問題は、色々な解き方があるけれど、どの問題が出てきても解くことができるように、繰り返し問題を解いて全てのパターンをマスターしよう!
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。

-
-
この前は詳しく解説していただいてありがとうございました!
とっても助かりました!
今は一次関数に入っていて・・・
・直線y=-3x+6とx軸について対象な直線
・y=-3x+5 ただしx<0のyの変域を求めなさい
の二つを教えてほしいです!解説を読んでも理解できなくて・・


明日定期テスト2日目で数学があり、なんと範囲が一次関数なんです。数学の先生の教え方が僕に合わずあまり理解できず、とても不安だったのですがとても分かりやすかったです。ありがとうございます。明日頑張りたいと思います。