「二元一次方程式のグラフの書き方」をわかりやすく解説
中学2年生の数学で学習する「二元一次方程式とグラフ」について、二元一次方程式からグラフを書く方法をわかりやすく解説するよ。
二元一次方程式とはなんだったかの復習もするので、安心してね。
二元一次方程式とは
連立方程式の時にも登場した二元一次方程式を覚えているかな?
もしかしたら、「忘れてしまった……」という人もいるかもしれないから、まずは復習をしよう!
元とは、方程式で見るχやyのような未知数のことなんだ。
元の前についている数字は、未知数の数を表しているよ。
だから「二元」というのは、未知数が2つということなんだ。
つまり二元一次方程式とは、「正体不明の文字が2文字(χやy、aやbなど)入っている方程式」のことだよ。
二元一次方程式の例
2χ+y=2、-3χ+4y=-3
次に二元一次方程式の解について確認するよ。
二元一次方程式の解は、1つではなくいくつもあることが特徴なんだ。
実際に例題で確認してみよう。
例題
-χ+2y=2の解を求めなさい。
この問題では、χに色々な値を代入してyの値を求める、という解き方をするよ。
今回は、χに0、1、2、3、4を代入した場合で考えてみよう。
| χの値 | 代入した式 | yの値 |
| χ=0 | -1×0+2y=2 | y=1 |
| χ=1 | -1×1+2y=2 | y=\(\frac{3}{2}\) |
| χ=2 | -1×2+2y=2 | y=2 |
| χ=3 | -1×3+2y=2 | y=\(\frac{5}{2}\) |
| χ=4 | -1×4+2y=2 | y=3 |
こんな風に二元一次方程式では、複数のχとyの組み合わせができるよ。
二元一次方程式について忘れていた人は、思い出せたかな?
まだ自信がないという人は、「連立方程式(二元一次方程式)の解き方「加減法・代入法」を解説」を確認しよう。
二元一次方程式のグラフをかいてみよう
さっきの例題を使って、二元一次方程式のグラフがどんな直線になるのかを見ていこう。
まずは、例題の二元一次方程式-χ+2y=2の解の値を座標として考えて、かいてみよう。
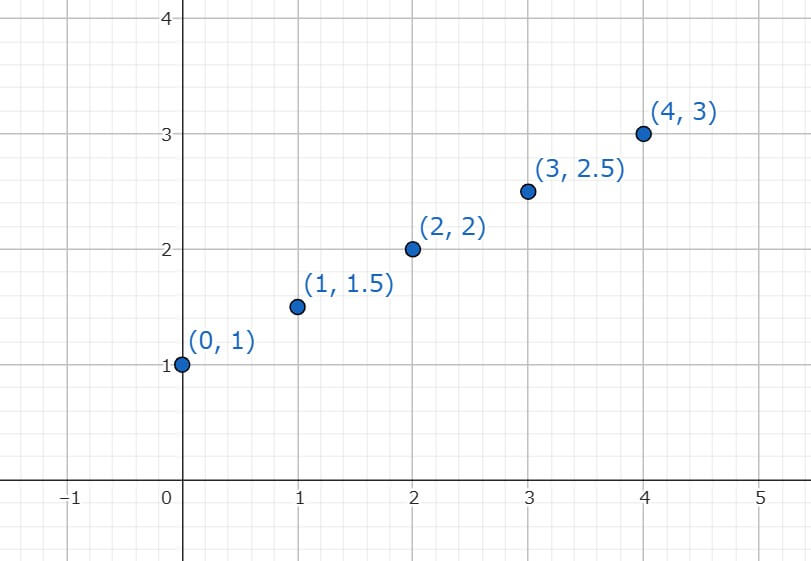
※\(\frac{3}{2}\)は1.5、\(\frac{5}{2}\)は2.5としているよ。
この点を全て結ぶと一次関数の直線になるね!
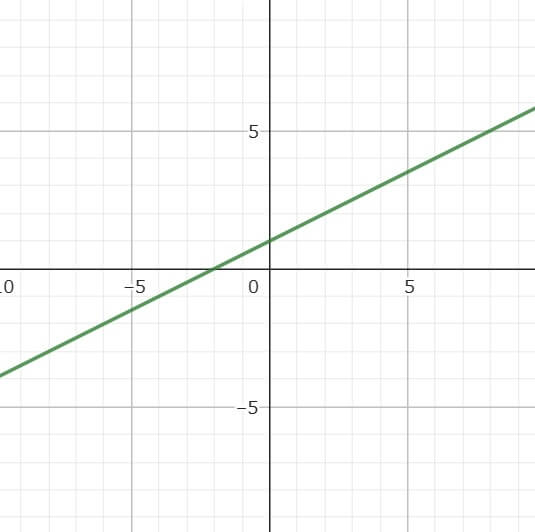
例題の二元一次方程式の-χ+2y=2をyについて解いてみると
-χ+2y=2
↓-χを左辺に移項(移項した-χの符号を変えることを忘れずに!)
2y=χ+2
↓両辺に\(\frac{1}{2}\)をかけて、yの前の数字を1にして「y=」に変形
y=\(\frac{1}{2}\)χ+1
傾きが\(\frac{1}{2}\)、切片が1の一次関数の形になって、上のグラフと計算で求めた式が一致しているね!
テストでも例題のような二元一次方程式の式のグラフをかく問題が出るんだけれど、
「y=」の形にして傾きと切片を求めると簡単にかくことができるよ。
この考え方を使って問題にチャレンジしよう!
問題
次の(1)から(4)のグラフをかきなさい。
(1)2χ+y=4
(2)χ-3y=-6
(3)2χ+5y-15=0
(4)\(\frac{χ}{4}\)+\(\frac{y}{3}\)=-1
(1)から(4)の式を「y=」の形に変形して、傾きと切片を求めるところからスタートしよう。
(1)y=-2χ+4 傾き-2、切片4
(2)y=\(\frac{1}{3}\)χ+2 傾き\(\frac{1}{3}\)、切片2
(3)y=-\(\frac{2}{5}\)χ+3 傾き-\(\frac{2}{5}\)、切片3
(4)y=-\(\frac{3}{4}\)χ-3 傾き-\(\frac{3}{4}\)、切片-3
傾きと切片がわかるとグラフは簡単にかくことができるよ。
一次関数のグラフのかき方
①切片の座標をスタート地点にする。
②傾きを分数の形にして\(\frac{上下に進む数}{右に進む数}\)と考えて、直線が通る2つ目の座標を見つける。
※傾きが整数の時は、分母は1になるよ。
傾きが2⇒\(\frac{2}{1}\)のように考えよう。
③①と②の座標を結んでグラフをかく。
グラフのかき方を参考にして、(1)から(4)のグラフをかこう。
※(1)だけかき方の手順を使って説明するよ。
(2)から(4)は、自分でかいたものと答えを見比べてみよう。
(1)
①切片は4だから、(0、4)の座標をかく。
②傾きが-2だから、\(\frac{-2}{1}\)と考えて、切片から右に1、下に2進んだ点をかく。
③①と②の点を結ぶ。
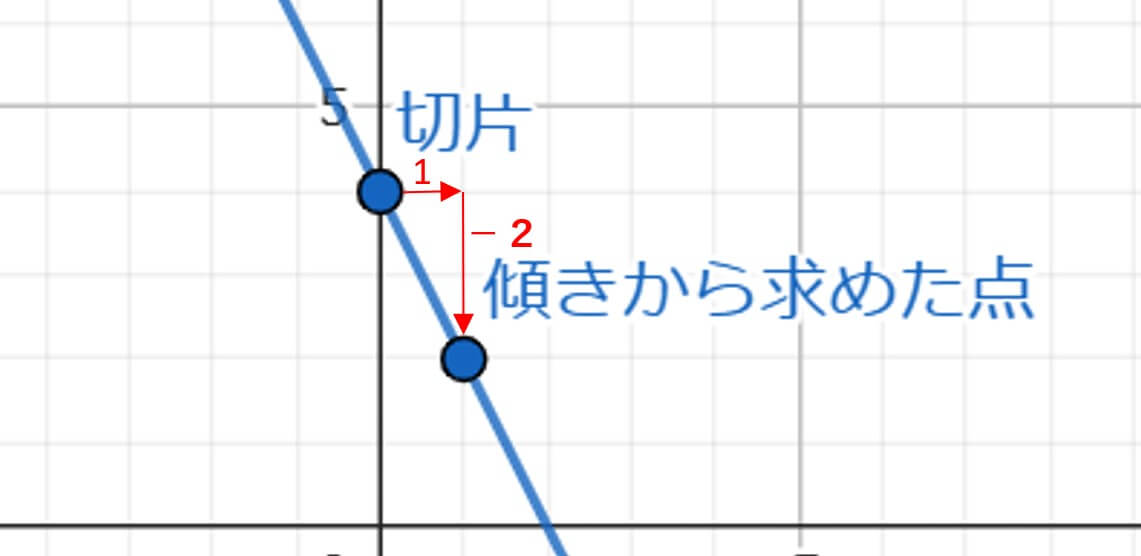
さっきの手順を使うと簡単にグラフをかくことができるから、参考にしてね。
(1)から(4)の答え
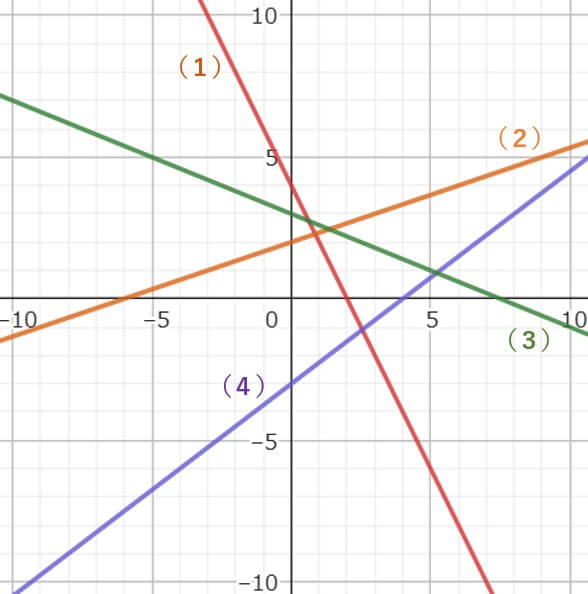
次にちょっと変わった二元一次方程式を紹介するね。
例題
次の(1)(2)のグラフをかきなさい。
(1)2χ=4
(2)2y+6=0
(1)ではyがなくて、(2)ではχがない式だけれど、この2つも実は二元一次方程式なんだ。
最初の説明で二元一次方程式は、「正体不明の文字が2文字(χやy、aやbなど)入っている方程式」と伝えていたから、間違えているように思った人も多いよね。
実は(1)は2χ+0y=4、(2)0χ+2y+6=0として考えるんだ。
じゃあ、このグラフが一体どんな形になるのかを見ていこう。
(1)
yがなくて「y=」の形にはできないから、この場合は「χ=」の形に変形するんだ。
そうすると、今回の式はχ=2となるね。
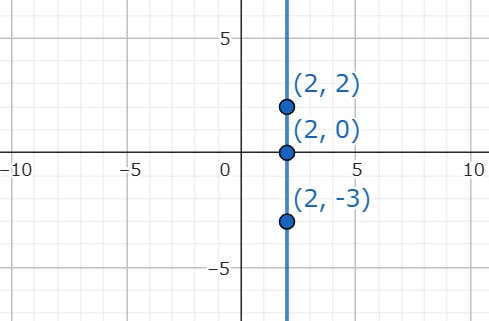
このyがない式は、yがどんな値でもχは絶対に2を通る、というグラフになるということを意味しているんだ。
つまり、(2、0)(2、-3)(2、2)のように、χが2だったらyはなんでもOKということだよ。
この点を全てかいて結ぶと、下のようなy軸に平行な縦一直線のグラフになるよ。
(2)
χがないけれど、これまでと同じように「y=」の形に変形するところからスタートしよう。
そうすると、今回の式はy=-3となるね。
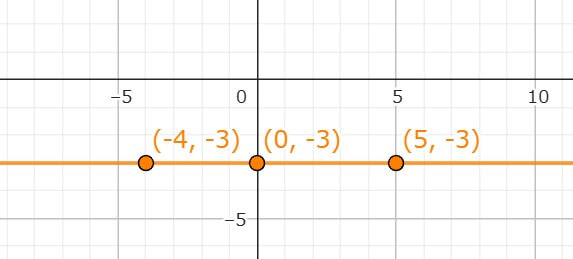
このyがない式は、χがどんな値でもyは絶対に-3を通る、というグラフになるよ。
つまり、(0、-3)(-4、-3)(5、-3)のように、yが-3だったらχはなんでもOKということだよ。
この点を全てかいて結ぶと、下のようなχ軸に平行な横一直線のグラフになるよ。
二元一次方程式のグラフは、特別な場合(χ=2やy=-3のように文字が1つの式の場合)を除いて、一次関数のグラフと同じかき方ができるんだ。
特別な場合(文字が1つの式の場合)も、通る点がわかるとグラフをかくことができるね。
どのパターンがテストに出てもグラフをかくことができるように、色々な問題にチャレンジして、二元一次方程式のグラフのかき方をマスターしよう!
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。



めっちゃわかりやすかったです!
期末頑張りたいと思います!