平行四辺形になるための条件5つとは?証明問題の解き方を解説
中学2年生の数学で学習する「平行四辺形になるための条件」について、平行四辺形の定理の逆を証明しながら、平行四辺形になるための5つの条件とは何かを解説するよ。
平行四辺形になるための条件を使った証明問題の解き方もくわしく紹介。
「平行四辺形では、2組の対辺はそれぞれ等しい」の逆を証明してみよう
二等辺三角形になるための条件を確かめた時のように、平行四辺形でも同じように定理の「逆」が正しいことを証明して「平行四辺形になるための条件」を確認しよう!
まずは「平行四辺形では、2組の対辺はそれぞれ等しい」ことの逆の「2組の対辺がそれぞれ等しい四角形は、平行四辺形である」を証明しよう。
仮定は「四角形の2組の対辺はそれぞれ等しい(AB=DC、AD=BC)」となるよ。
結論である「平行四辺形」ということを証明するというのは、定義である「2組の対辺が平行」が成り立つことを証明すれば良いということだよ。
※2辺が平行であることを証明するには、錯角や同位角が等しいことを証明すれば良かったよね。
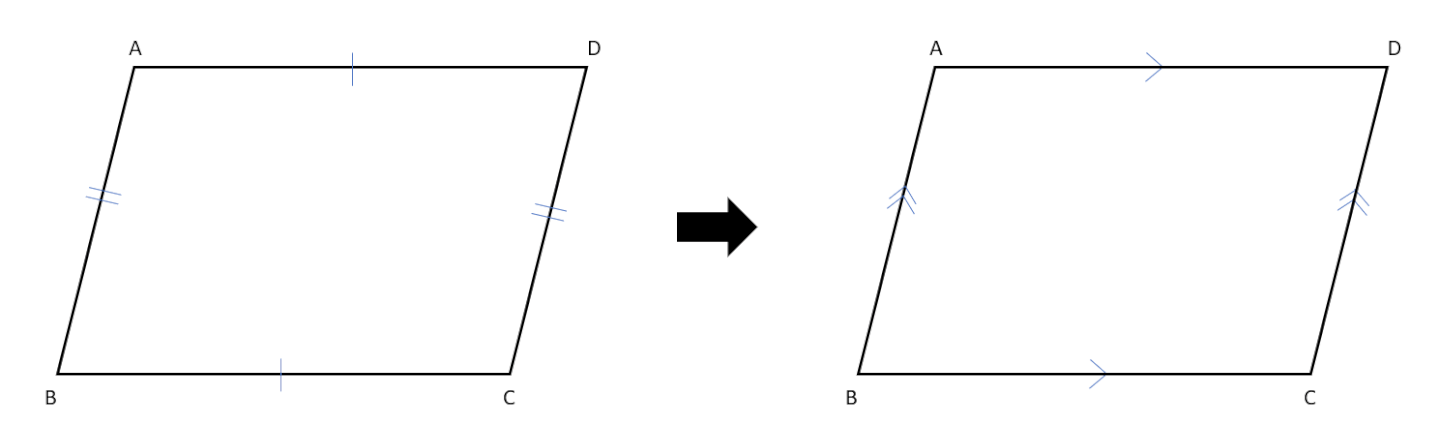
今回の証明では下の図のように四角形ABCDの頂点BとDを結んで、∠ADBと∠CBD、∠ABDと∠CDBが等しくなることを証明していこう。
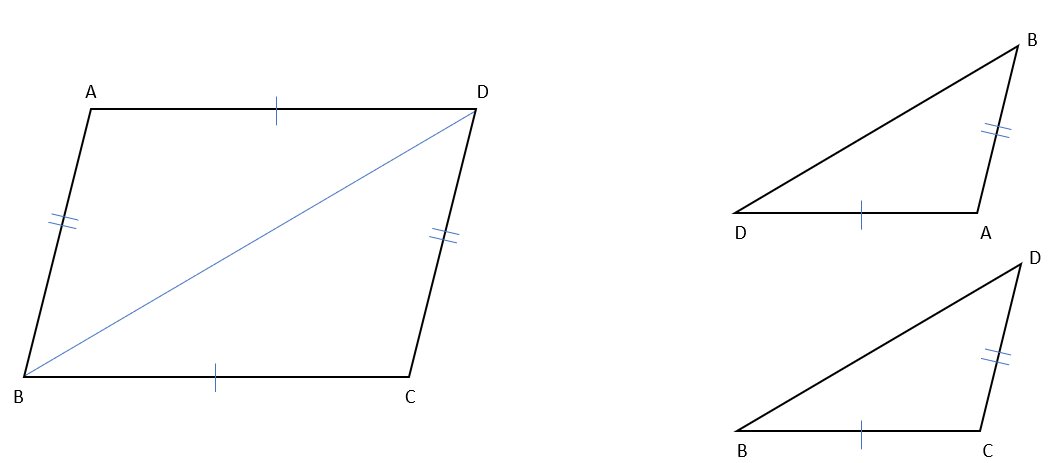
△ADBと△CBDにおいて
仮定から
AB=CD・・・①
DA=BC・・・②
また、BDは共通・・・③
①、②、③より、
3組の辺がそれぞれ等しいから
△ADB≡△CBD
合同な図形の対応する辺は等しいから
∠ADB=∠CBD、∠ABD=∠CDB
錯角が等しいから
AD∥CB、AB∥DC
2組の対辺がそれぞれ平行だから
四角形ABCDは平行四辺形である。
「2組の対辺がそれぞれ等しい四角形は、平行四辺形である」を証明することができたね。
つまり、「2組の対辺がそれぞれ等しい」は、「平行四辺形になるための条件」といえるよ。
「平行四辺形では、2組の対角はそれぞれ等しい」の逆を証明してみよう
次に「平行四辺形では、2組の対角はそれぞれ等しい」ことの逆の「2組の対角がそれぞれ等しい四角形は、平行四辺形である」を証明しよう。
仮定は「四角形の2組の対角はそれぞれ等しい(∠DAB=BCD、∠ABC=∠CDA)」となるよ。
結論である「平行四辺形」ということを証明するというのは、定義である「2組の対辺が平行」が成り立つことを証明すれば良いということだよ。
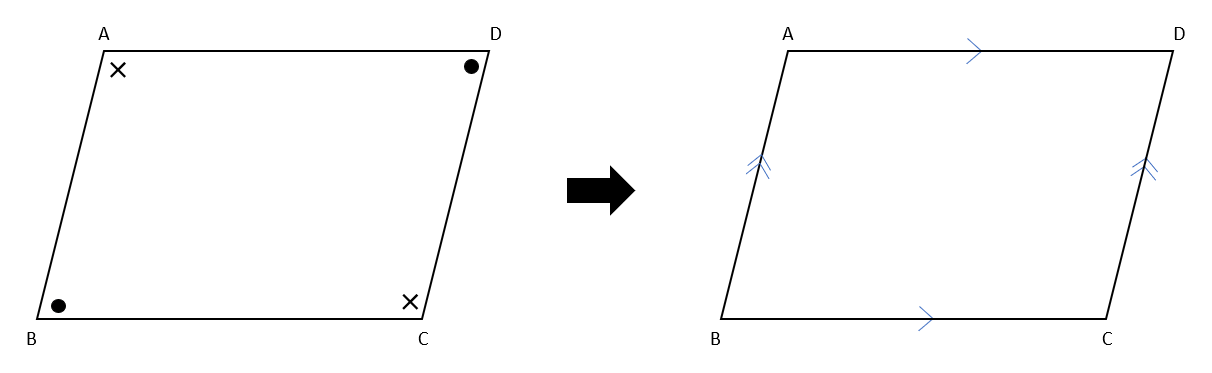
この証明は三角形は使わずに、四角形の内角の和や一直線が作る角を使って証明していくよ。
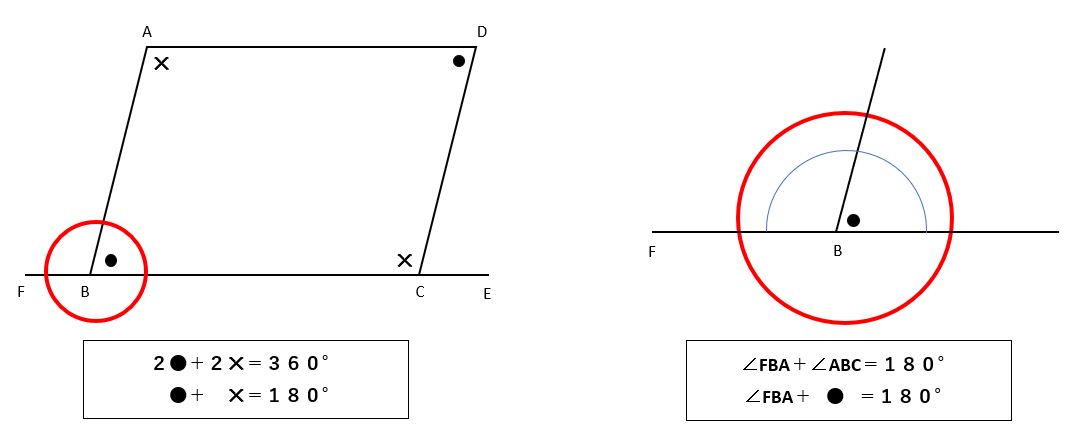
辺BCの延長線上に点Fをとって証明していくよ。
四角形の内角の和は、360°だから
∠DAB+∠ABC+∠BCD+∠CDA=360°
仮定から、∠DAB=BCD、∠ABC=∠CDAであるから
∠DAB+∠DAB+∠ABC+∠ABC=360°
したがって、∠DAB+∠ABC=180°・・・①
(上の左側の図と合わせて確認しよう)
また、一直線が作る角は180°となるので、
∠FBA+∠ABC=180°・・・②
(上の図の赤い丸で囲った部分と合わせて確認しよう)
①、②から∠DAB=∠FBA・・・③
錯角が等しいから
AD∥BC・・・④
仮定の∠DAB=∠BCDと③より
∠FBA=∠BCD
同位角が等しいから
AB∥DC・・・⑤
④、⑤より、2組の対辺がそれぞれ平行だから
四角形ABCDは平行四辺形である。
「2組の対角がそれぞれ等しい四角形は、平行四辺形である」を証明することができたね。
つまり、「2組の対角がそれぞれ等しい」は、「平行四辺形になるための条件」といえるよ。
「平行四辺形では、対角線はそれぞれの中点で交わる」の逆を証明してみよう
「平行四辺形では、対角線はそれぞれの中点で交わる」ことの逆の「対角線がそれぞれの中点で交わる四角形は、平行四辺形である」を証明しよう。
仮定は「四角形の対角線はそれぞれの中点で交わる(AO=CO、BO=DO)」となるよ。
結論である「平行四辺形」ということを証明するというのは、定義である「2組の対辺が平行」が成り立つことを証明すれば良いということだよ。
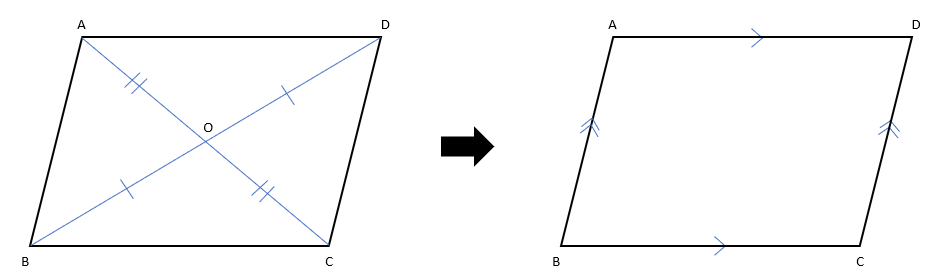
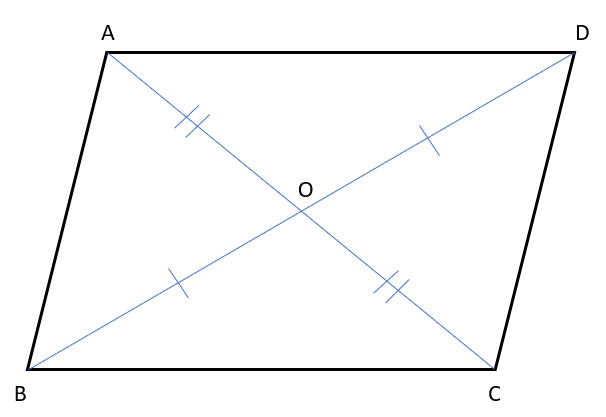
この証明では、∠ABOと∠CDO、∠DAOと∠BCOが等しくなることを証明していくよ。
まずは、△AOBと△CODが合同であることを証明して、∠ABOと∠CDOが等しくなることを証明しよう。
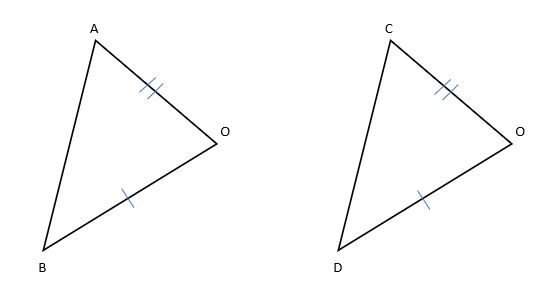
△AOBと△CODにおいて
仮定から
AO=CO・・・①
BO=DO・・・②
また、対頂角は等しいので
∠AOB=∠COD・・・③
①、②、③より
2組の辺とその間の角がそれぞれ等しいから
△AOB≡△COD
合同な図形の対応する角は等しいから
∠ABO=∠CDO
錯角が等しいので、
AB∥CD
同様にして、
△AOD≡△COBより
合同な図形の対応する角は等しいから
∠DAO=∠BCO
錯角が等しいので、
AD∥BC
2組の対辺がそれぞれ平行だから、四角形ABCDは平行四辺形である。
※この証明で出てきた「同様にして」という言葉は、同様な手順で証明できる場合に使うことができるよ。
「対角線がそれぞれの中点で交わる四角形は、平行四辺形である」を証明することができたね。
つまり、「対角線がそれぞれの中点で交わる」は、「平行四辺形になるための条件」といえるよ。
平行四辺形になるための条件
四角形が平行四辺形になるための条件は、平行四辺形の「定義」や「定理」、そして平行四辺形の性質の逆が正しいと証明できたものをまとめて、次のとおりになるよ。
平行四辺形になるための条件
・2組の対辺がそれぞれ平行である。
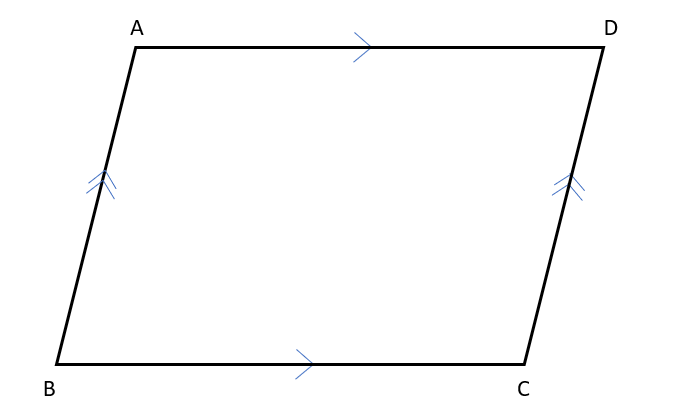
・2組の対辺がそれぞれ等しい。
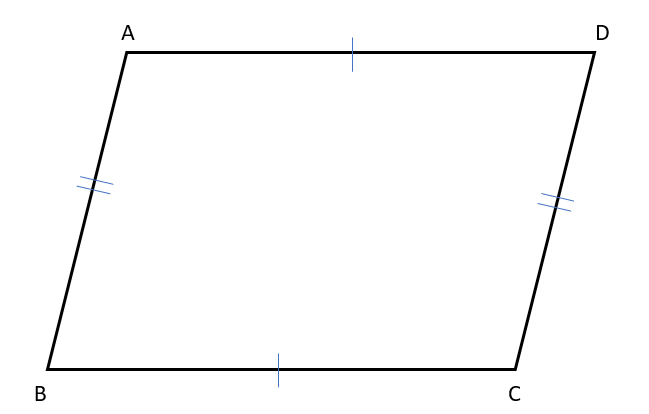
・2組の対角がそれぞれ等しい。
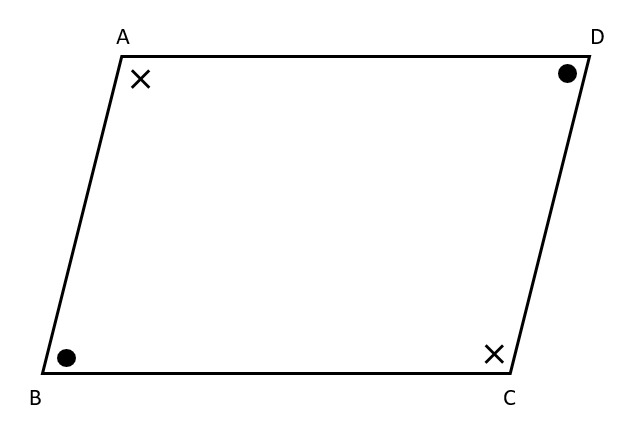
・対角線がそれぞれの中点で交わる。
また、定理では出てこなかったもので、もう1つ平行四辺形になる条件があるから紹介するね。
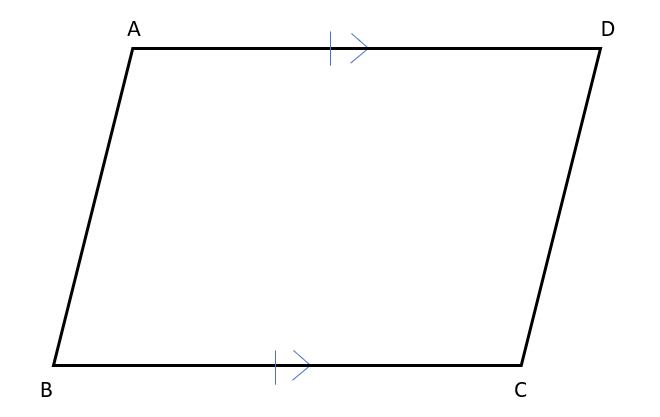
それは、「1組の対辺が平行でその長さが等しい」という条件なんだ。
実際に証明して確認していこう。
下の図のように四角形ABCDの頂点BとDを結んで、∠ABDと∠CDBが等しくなることを証明していこう。
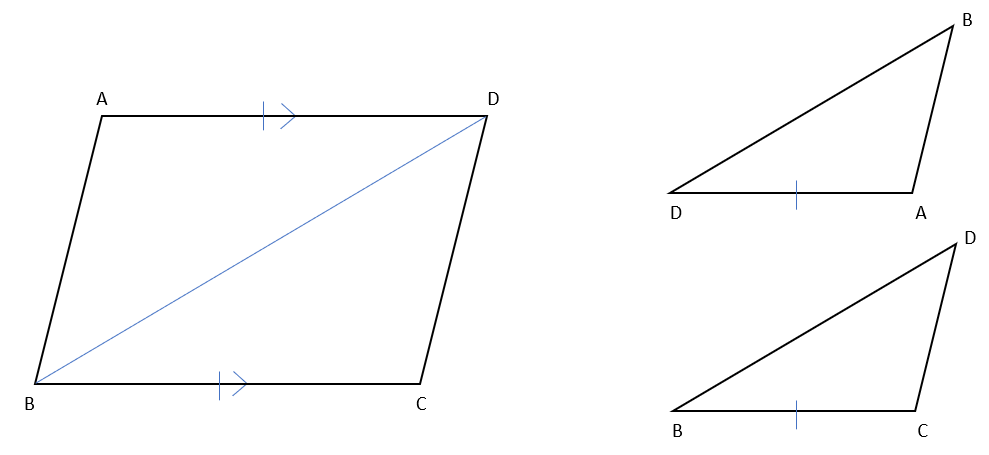
△ABDと△CDBにおいて
仮定から
AD=CB・・・①
BDは共通・・・②
AD∥CBより、平行線の錯角は等しいから
∠ADB=∠CBD・・・③
①、②、③より
2組の辺とその間の角がそれぞれ等しいから
△ABD≡△CDB
合同な図形の対応する角は等しいから
∠ABD=∠CDB
錯角が等しいので、
AB∥DC
AD∥CB、AB∥DCより
2組の対辺がそれぞれ平行だから、四角形ABCDは平行四辺形である。
このように証明できるから、「1組の対辺が平行でその長さは等しい」は、「平行四辺形になるための条件」といえるよ。
平行四辺形になるための条件
・1組の対辺が平行でその長さが等しい。
平行四辺形になるための5つの条件は、テストにもよく出題されるから確実に覚えておこう。
平行四辺形になるための条件を使った証明問題
平行四辺形になるための条件を使った証明問題にチャレンジしよう。
問題
平行四辺形ABCDの辺BC、AD上に2点E、Fをとります。
この時、∠BAE=∠DCFならば、四角形AECFが平行四辺形となることを証明しなさい。
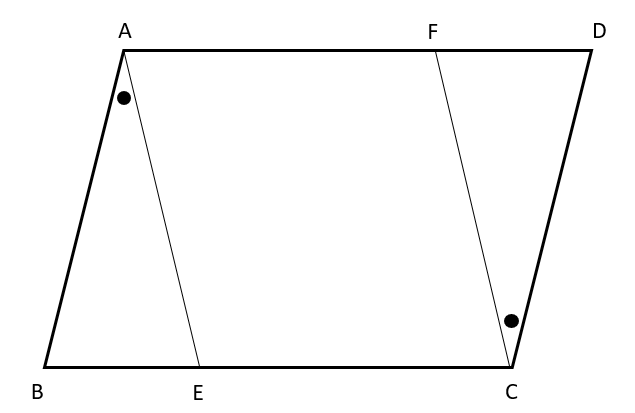
①仮定と結論を問題文から見つけよう。
仮定
∠BAE=∠DCF
四角形ABCDが平行四辺形である
結論
四角形AECFが平行四辺形
結論は簡単に見つけることができるけれど、平行四辺形になるためのどの条件を使うか迷ってしまうね。
今回は、「2組の対辺がそれぞれ等しい」を使って証明していこう。
そのために、△ABEと△CDFの合同を証明していくよ。
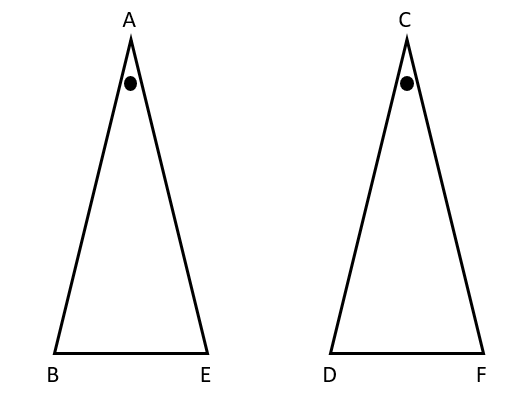
②仮定からわかることを書こう。
四角形ABCDが平行四辺形だから、
AB=CD(平行四辺形の対辺が等しいから)
∠ABE=∠CDF(平行四辺形の対角が等しいから)
を使うことができるよ。
証明
△ABEと△CDFにおいて
仮定から、
∠BAE=∠DCF・・・①
平行四辺形の対辺は等しいので、
AB=CD・・・②
また、平行四辺形の対角は等しいので、
∠ABE=∠CDF・・・③
①、②、③より
1組の辺とその両端の角がそれぞれ等しいから
△ABE≡△CDF
合同な図形の対応する辺は等しいので
AE=CF・・・④
BE=DF・・・⑤
平行四辺形の対辺は等しいので、
AD=BC・・・⑥
⑤、⑥より
ADーDF=BCーBE
よって、
AF=EC・・・⑦
④、⑦から2組の対辺がそれぞれ等しいので、
四角形AECFは平行四辺形となる。
今回の問題のように、ひき算を使って辺や角が等しいことを証明することがあるから覚えておこう。
「平行四辺形になるための条件」まとめ
・平行四辺形になるための条件は全部で5つある。
①2組の対辺がそれぞれ平行である。
②2組の対辺がそれぞれ等しい。
③2組の対角がそれぞれ等しい。
④対角線がそれぞれの中点で交わる。
⑤1組の対辺が平行でその長さが等しい。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。



めっちゃわかりやすかったです