二等辺三角形の性質と定理「定義・定理」とは?わかりやすく解説
中学2年生の数学で学習する「二等辺三角形の性質・定理」について、「定義」とはなにか、「定理」とはなにか?二等辺三角形の定理はどのようなものがあるのかをわかりやすく解説するよ。
「定義」とは
数学には色々な用語があるけれど、新しい用語で「定義」とはどういう意味の用語かを紹介するね。
教科書では、
定義とは、ことばの意味をはっきり述べたもの
と書かれているんだけれども、なんとなくピンとこないね。
たとえば、身近なことでたとえると、「雨」ということばがあるよね。
雨の定義は、「広範囲にわたって空から降ってくる水滴」となるんだ。
辞書で、言葉の下にある「その言葉はどんな意味かを説明しているもの」のイメージかな。
数学で「定義」と使う時は、「数学で使われている用語の意味を表すもの」と覚えておこう。
これまでに出てきた数学の用語の定義を少し紹介するね。
| 用語 | 定義 |
| 偶数 | 2で割り切れる整数 |
| 奇数 | 2で割り切れない整数 |
| 対頂角 | 2つの直線によって角が作られるとき、向かい合っている角のこと |
証明の単元では色々な図形が出てくるけれど、それぞれの図形の定義(その図形は、どういう図形か)を確認していくから楽しみにしていてね。
二等辺三角形の性質
ここからは二等辺三角形について勉強していくよ。
まずは、二等辺三角形について、上で紹介した「定義」を確認しよう!
二等辺三角形の定義 2つの辺が等しい三角形
漢字で書いたままの定義「二つの等しい辺の三角形」だね。
次に、二等辺三角形の辺の名前や角の名前についても確認するよ。
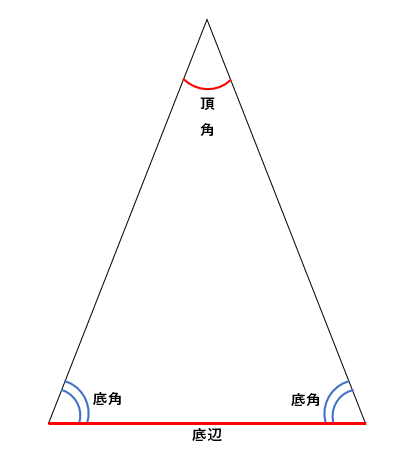
頂角 長さが等しい2つの辺の間の角
底辺 頂角と向かい合う辺
底角 底辺の両端の角
小学生で二等辺三角形について勉強した時に、「2つの辺が等しい」以外に非常に大切な性質を勉強したことを覚えているかな?
それは、「2つの角が等しい」という性質だよ。
この性質は、角度の計算問題だけではなく、証明問題でも非常によく使うから忘れずに覚えておこう!
「定理」とは
次は「定義」に似た用語で「定理」について確認するね。
定理とは証明されたことがらで、大切なもの
言葉の説明だけを見ると、わかるようなわからないような・・・
ひと言でいうとこれは「性質」のことなんだ。
これまで登場した定理では、
三角形の定理 三角形の内角の和は180°
これも定理の1つなんだ。
ちなみに、「定理」については、「定義」を使って証明することができるよ。では早速、二等辺三角形の定理について確認していこう。
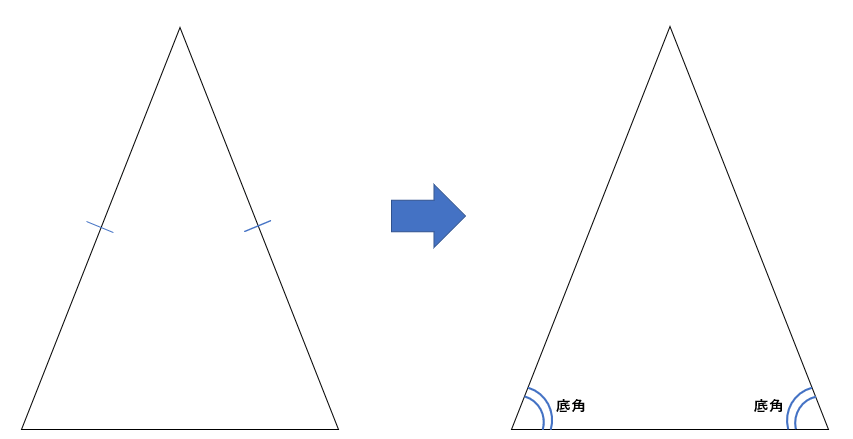
二等辺三角形の底角の定理
二等辺三角形には2つの定理があるんだけれども、1つ目は底角に関する定理について説明するよ。
二等辺三角形の定理① 二等辺三角形の底角は等しい
この定理について、二等辺三角形の定義「2つの辺が等しい三角形」を使って証明してみよう。
例題
下の図の△ABCがAB=ACの二等辺三角形、辺ADが∠ABCの二等分線ならば∠ABD=∠ACDとなることを証明しなさい。
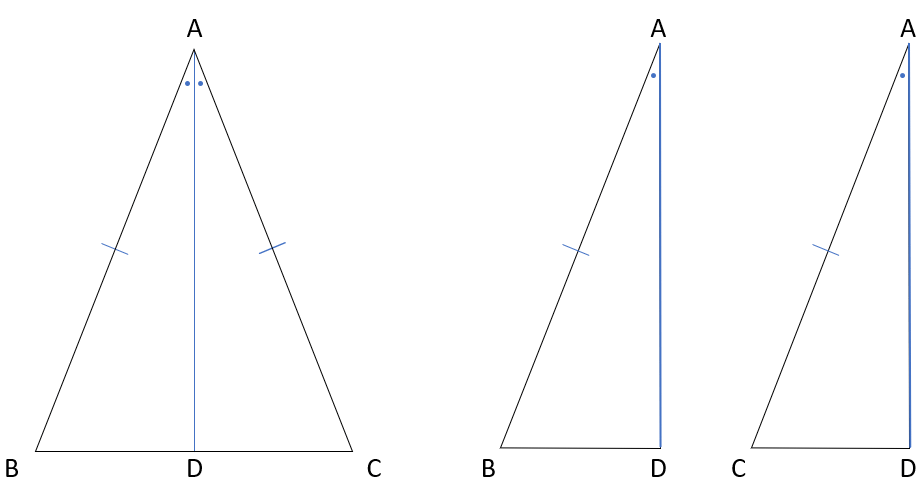
「証明のやり方と書き方」のコツは?で説明した手順で解いていくよ。
証明に必要な△ABDと△ACDの図もかいたから、対応する辺や角の対応順を考える時の参考にしてね。
①仮定と結論を問題文から見つけよう。
仮定 △ABCがAB=ACの二等辺三角形、辺ADは∠ABCの二等分線
結論 ∠ABD=∠ACD
②仮定からわかることを書こう。
AB=AC
辺ADが∠ABCの二等分線だから、∠BAC=∠CAD
③すでに正しいと認められていることがらを図形を見て探そう
上の図を見ると、ADがどちらの図形にも重なっているから、AD=AD
※ちなみに、ぴったり重なっている辺や角を「●●は共通」と表現するから覚えておこう!(共通な辺・角は等しいので、と書く場合もあるから、学校で習ったルールで書くようにしよう。)
④三角形の合同条件のどれに当てはまるかを考えよう。
①~③から、「2組の辺とその間の角がそれぞれ等しい」という合同条件に当てはまることがわかるね。
⑤結論が証明されたことを書こう。
今回の問題の結論は、∠ABD=∠ACDということが言えればOKだから、
「合同な図形の対応する角が等しいので∠ABD=∠ACD」
と証明の時に書こう。
証明
△ABDと△ACDにおいて
仮定から、AB=AC・・・①
辺ADが∠ABCの二等分線だから、∠BAC=∠CAD・・・②
ADは共通・・・③
①、②、③より、2組の辺とその間の角がそれぞれ等しいから、
△ABD≡△ACD
合同な図形の対応する角は等しいから
∠ABD=∠ACD
これで定理の1つ目の二等辺三角形の底角は等しいことが証明できたよ。
もう1つの定理も同じように証明して確認しよう。
二等辺三角形の頂角の二等分線の定理
二等辺三角形の2つ目の定理は、頂角の二等分線に関する定理だよ。
二等辺三角形の定理② 二等辺三角形の頂角の二等分線は、底辺を垂直に2等分する。
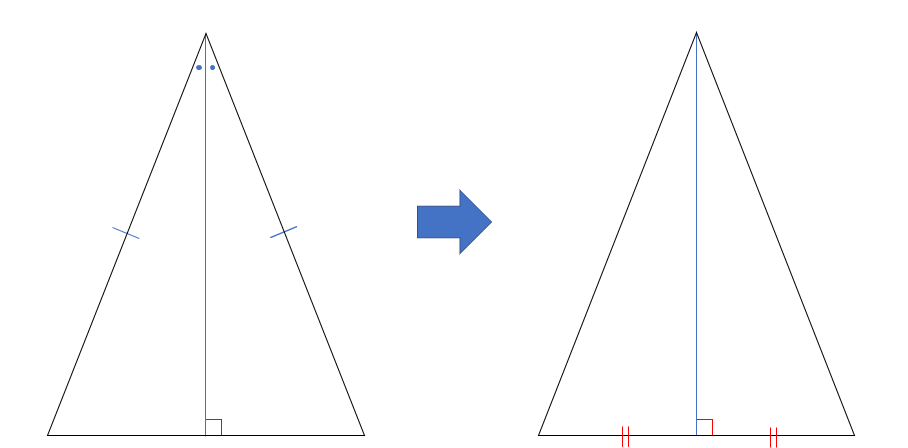
この定理についても上と同じように証明をしていくんだけれども、二等辺三角形の底角が等しいことを証明した流れの△ABD≡△ACDまで全く同じなんだ。
だから、そこまでは省略して証明をするね。
証明
△ABD≡△ACDより
合同な図形の対応する辺は等しいから、BD=CD
また、合同な図形の対応する角は等しいから、∠ADB=∠ADC
∠ADB+∠ADC=180°なので
∠ADB=∠ADC=90°
よって、AD⊥BCとなる。
この証明で二等辺三角形の頂角の二等分線は、底辺を垂直に2等分することが証明されたけれども、もう少し詳しく説明するね。
上の証明でBD=CDということを書いたけれども、これは下の図のように「DがBCの中点」になることを表しているよ。
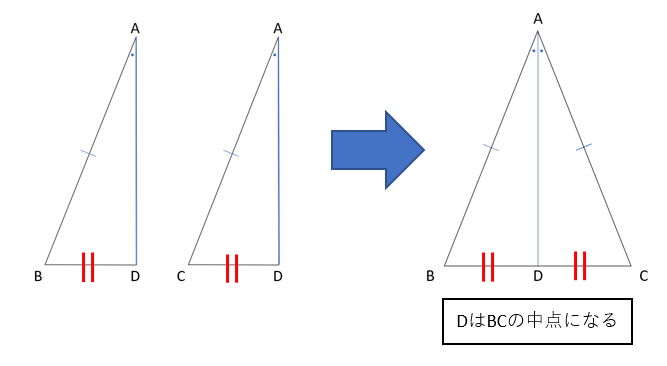
次に∠ADB=∠ADC=90°がなるのは、一直線は180°という性質を使っているよ。
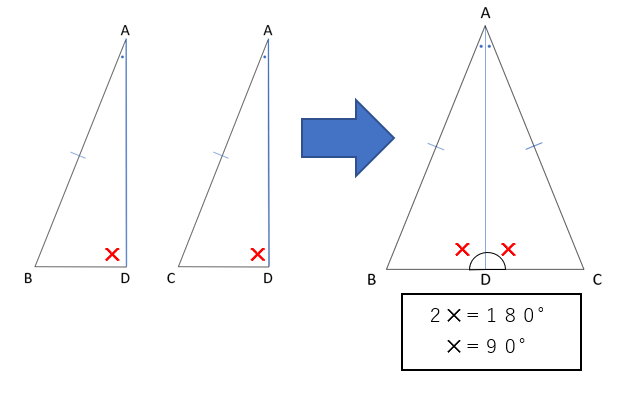
ちなみに「定義」「定理」は、証明の中で「すでに正しいと認められていることがら」として使うことができるから、しっかりと覚えておこう!
二等辺三角形の性質(定義・定理とは)まとめ
- 定義とは、ことばの意味をはっきり述べたもの
例:「二等辺三角形」ということばの定義は「二つの辺が等しい三角形」 - 定理とは証明されたことがらで、大切なもの
例:「三角形の内角の和は180°」は、三角形の定理 - 二等辺三角形の定理①
二等辺三角形の底角は等しい - 二等辺三角形の定理②
二等辺三角形の頂角の二等分線は、底辺を垂直に2等分する。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。


