放物線とは?「yはxの二乗に比例する」グラフの書き方を解説
中学3年生の数学で学習する「yはxの二乗に比例する(y=ax2)」グラフの書き方をわかりやすく解説するよ。
y=ax2のグラフは、どのような形になるのか?
比例定数が増えたときや、比例定数が負の数のときにはどのような形になるのか?
「放物線」とはどんなものか、くわしく紹介していくよ。
y=x2のグラフはどんな特徴があるのか?
中学数学で学習してきた関数のグラフを復習しよう。
まずは1年生の数学で学習した「比例のグラフ」
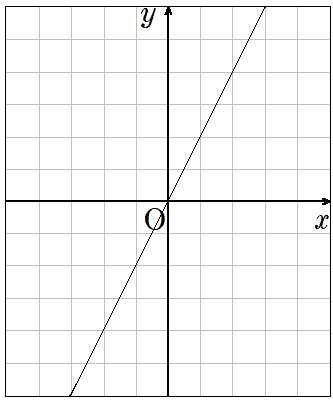
比例のグラフは、直線で、原点を必ず通るなどの特徴があったね。
「反比例のグラフ」
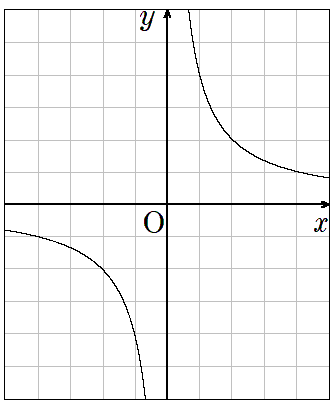
反比例のグラフは、原点を通らなくて、x軸とy軸をまたがなかったね。「双曲線」と呼ばれる2つの曲がった線がかならずできるんだったね。
2年生の数学で学習した「一次関数のグラフ」
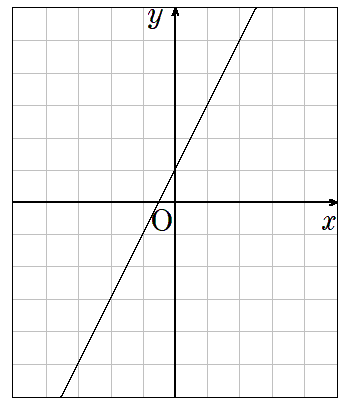
一次関数(y=ax+b)のグラフは、比例のグラフと同じで直線だけれど、「切片」でy軸と交わり、原点を通らない特徴があったね。
さて、いよいよ本題。
3年生の数学で学習するのは「yはxの二乗に比例する関数のグラフ」だよ。
名前だけだとピンとこないね。
実際に、どんなグラフになるのかを考えていこう。
「yはxの二乗に比例する関数」は「y=ax2」と表すことができるんだったよね。
今回は比例定数「a=1」だと仮定してグラフを書いてみよう。
y=x2のグラフを書いてみよう
①から③の手順でy=x2のグラフを書こう。
①表をうめる
y=x2の「x」に-3から3までの値を代入して「y」の値を求めよう。
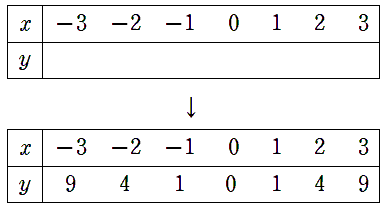
②座標をとる
表を縦にみて、xとyの座標をグラフにとろう
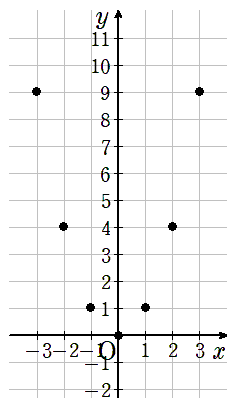
③線で結ぶ
座標を線で結ぼう。
ここで「yはxの二乗に比例する関数」のポイント。
「yはxの二乗に比例する関数」は直線ではなく、曲線(曲がった線)になるんだ。
だから定規を使って書いちゃいけないんだ。
こんな感じになるよ。
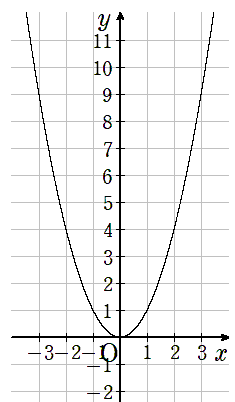
y=x2のグラフが曲線になる理由
じゃあ、なんで曲線になるかを考えていこう。
さっきの表をもっと細かくとってみたよ。

「x」と「y」の座標をとると、なんと「なめらかな曲線」っぽくなることがわかるかな。
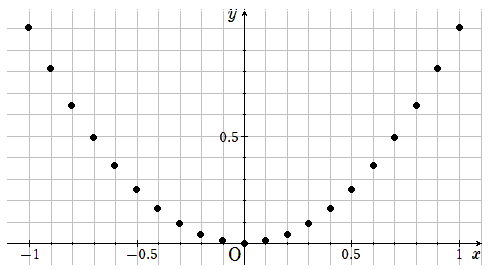
たとえば、「y=ax2」の式になる例として、「坂道を転げ落ちるボール」をイメージしてみよう。
ボールの転げ落ちるスピードは、どんどん加速していくよね。
でも、この加速って、「なめらかに、だんだんと加速していく」よね。
けっして、スピードが速くなるたびに「ガクン、ガクン」とスピードの早さが変わったりしないよね。
だから、グラフの線もカクカクしない、なめらかな曲線になるんだよ。
反比例のグラフと同じで、「yはxの二乗に比例する関数のグラフ」は曲線になること、定規を使って書いてはいけないということを覚えておこう。
y=x2のグラフの特徴
y=x2のグラフを見て特徴を考えてみよう。
この曲線は、y軸で折り曲げたらぴったり重なるよね。このことを「y軸対称」っていうよ。
あと原点(0,0)を通っているよね。
y=x2のグラフの特徴は次の通りだよ。
y=x2のグラフの特徴
- 必ず原点を通る
- なめらかな曲線になる
- y軸対称になる。
y=ax2のグラフの特徴
「yはxの二乗に比例する関数(y=ax2)」の比例定数「a」にはいろいろな数字が入るんだけれど、「a」の値が変わるとグラフがどのように変化していくかを考えていこう。
y=2x2のグラフ
まずはa=2のときのy=2x2を書いていこう。
①表をうめる
y=2x2の「x」に-3から3までの値を代入して「y」の値を求めよう。
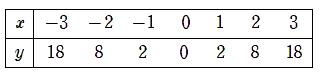
②座標をとる
表を縦にみて、xとyの座標をグラフにとろう
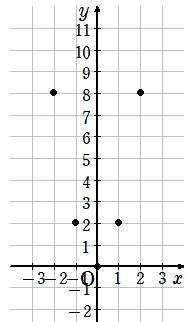
③曲線で結ぶ
座標をなめらかな曲線で結ぼう。
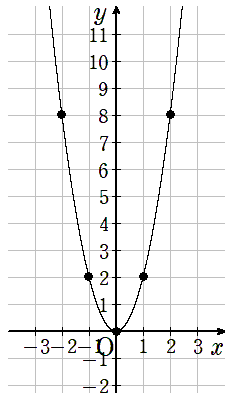
y=3x2のグラフ
次にはa=3のときのy=3x2を書いていこう。
①表をうめる
y=3x2の「x」に-3から3までの値を代入して「y」の値を求めよう。
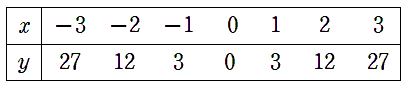
②座標をとる
表を縦にみて、xとyの座標をグラフにとろう
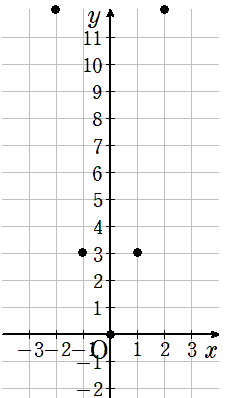
③曲線で結ぶ
座標をなめらかな曲線で結ぼう。
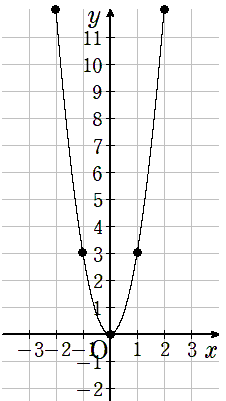
aの値によってグラフがどのように変化しているか
3つのグラフy=x2、y=2x2、y=3x2を今まで書いてきたね。
3つのグラフを比べると次のようになっているよ。
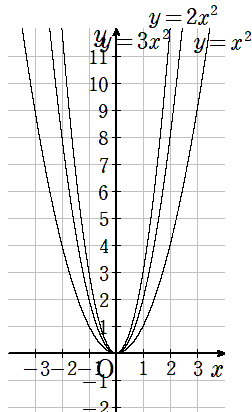
グラフを見てわかることは次の通りだね。
- aの値が1→2→3と増えると、グラフの開き方は小さくなる
- グラフは上に開いている
どうしてaの値が増えると、グラフの開き方は小さくなるのかというと、
「グラフの開き方が小さい」=より急な増え方なんだよね。
aの値が大きくなればなるほど、xが増えたときのyの増え方は急になるよね。
y=-ax2のグラフの特徴
じゃあ次に比例定数「a」がマイナス(負の数)になる場合のグラフについて考えていこう。
y=-x2のグラフ
まずはa=-1のときのy=-x2を書いていこう。
①表をうめる
y=-x2の「x」に-3から3までの値を代入して「y」の値を求めよう。

②座標をとる
表を縦にみて、xとyの座標をグラフにとろう
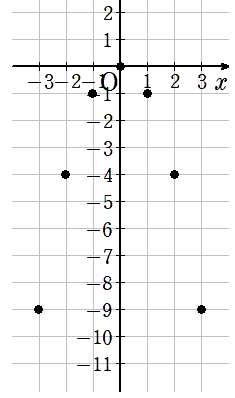
③曲線で結ぶ
座標をなめらかな曲線で結ぼう。
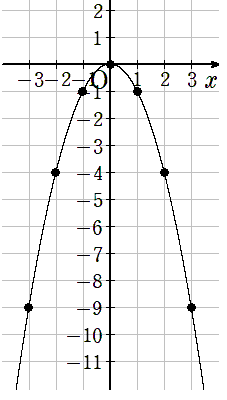
y=-2x2のグラフ
次にa=-2のときのy=-2x2を書いていこう。
①表をうめる
y=-2x2の「x」に-3から3までの値を代入して「y」の値を求めよう。

②座標をとる
表を縦にみて、xとyの座標をグラフにとろう
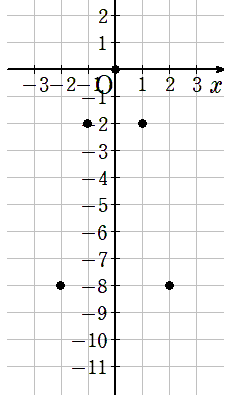
③曲線で結ぶ
座標をなめらかな曲線で結ぼう。
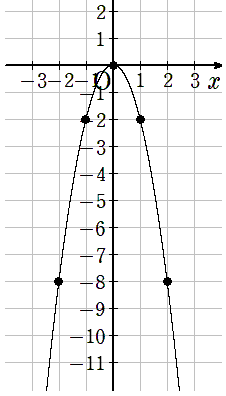
y=-3x2のグラフ
最後にa=-3のときのy=-3x2を書いていこう。
①表をうめる
y=-3x2の「x」に-3から3までの値を代入して「y」の値を求めよう。

②座標をとる
表を縦にみて、xとyの座標をグラフにとろう
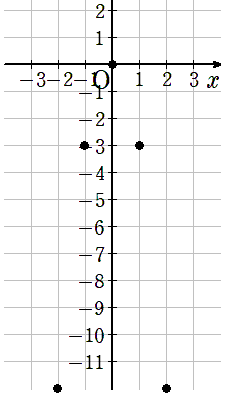
③曲線で結ぶ
座標をなめらかな曲線で結ぼう。
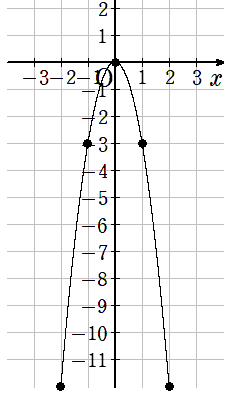
aの値によってグラフがどのように変化しているか
3つのグラフy=-x2、y=-2x2、y=-3x2を書いてきたね。
3つのグラフを比べると次のようになっているよ。
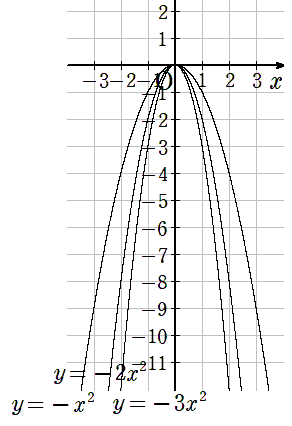
- aの値が-1→-2→-3と減ると、グラフの開き方は小さくなる
- グラフは下に開いている
今度は、aの値が減ると、グラフの開き方が小さくなるんだね。
比例定数がプラス(正の数)の時とは反対だね。
どうしてかというと、負の数の場合、数自体は減って「-1→-2→-3」と小さくなっていっていても、「a」の絶対値だけに注目すると、数字自体は「1→2→3」と大きくなっているよね。
つまり、やっぱり「急」になっているんだ。
xが減ったときの、yの減り方がより「急」になるので、グラフの開き方が小さくなるというわけだね。
y=ax2とy=-ax2のグラフの比較
比例定数「a」が正の場合と負の場合ではグラフはどのように変わってくるかをまとめてみよう。
今まで書いたグラフは次の通り。
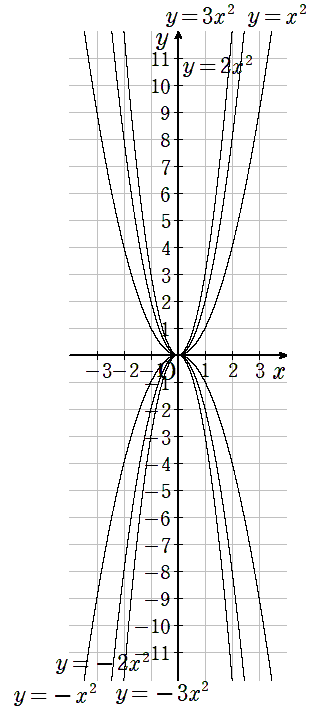
a>0(aがプラスの場合)
- グラフは上に開く
- aが大きくなると(1→2→3)、グラフの開きは小さくなる
a<0(aがマイナスの場合)
- グラフは下に開く
- aが小さくなると(-1→-2→-3)、グラフの開きは小さくなる
放物線とは
「yはxの二乗に比例する関数(y=ax2)」のグラフの形は、y軸を対称にしたなめらかな曲線だったね。
この曲線のことを、「放物線」と呼ぶよ。
「放物線」とは、「物を放ったときの線」という意味なんだ。
もう少しわかりやすく言うと、斜めに投げた物が落ちるまでに通る経路と同じ形の曲線ののことだよ。

よく野球とかで「美しい放物線を描いたホームラン」とか言ったりするよね。
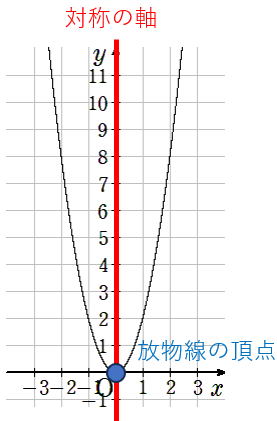
あまりテストでは出ることはないんだけれど、放物線の「頂点」や「対称の軸」という言葉も教科書に書いてあるので、覚えておこうね。
「yはxの二乗に比例する(y=ax2)」まとめ
y=x2のグラフの特徴
- 必ず原点を通る
- なめらかな曲線になる
- y軸対称になる。
a>0(aがプラスの場合)
- グラフは上に開く
- aが大きくなると(1→2→3)、グラフの開きは小さくなる
a<0(aがマイナスの場合)
- グラフは下に開く
- aが小さくなると(-1→-2→-3)、グラフの開きは小さくなる
放物線とは
- 「yはxの二乗に比例する関数(y=ax2)」のグラフの曲線のことを、「放物線」と呼ぶ。
- 「yはxの二乗に比例する関数(y=ax2)」のグラフが対称になっている軸(y軸)のことを、「対称の軸」と呼ぶ
- 「yはxの二乗に比例する関数(y=ax2)」のグラフの頂点となっている点(原点)のことを、「放物線の頂点」と呼ぶ
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。