「因数分解の公式一覧」公式を使った解き方をわかりやすく解説

中学３年生の数学で学習する「因数分解」について、因数分解の公式とはなにか、公式の使い方をわかりやすく解説するよ。

因数分解の公式は乗法公式がもとになっていることも紹介しているので、「なぜ因数分解の公式が使えるのか」を本質から理解することができるよ。

「因数分解の公式一覧」 公式を使った解き方をわかりやすく解説のPDF（11枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 乗法公式を逆に使って因数分解を解いてみよう
• 因数分解の公式
• 因数分解の公式一覧

乗法公式を逆に使って因数分解を解いてみよう

因数分解っていうのは展開の逆のことだったよね。

展開の学習の時に乗法公式を使ったのを覚えているかな？乗法公式を逆に使うと因数分解の時に役立つんだよ。

(x+2)(x+3) の展開を考えてみよう。

(x+a)(x+b)のような(x 　)(x 　 )の形の式を展開すると、x²+○x+△になるんだったよね。

○には2+3の和が、△には2×3の積が入るから

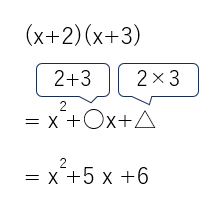
今の流れを逆にやっていくことが因数分解だよね。

x²+5x+6の因数分解

さっきの展開を逆に考えていこう。

x²+5x+6を(x＋□)(x+☆)の形にできたら因数分解の完成だよ。下を見て□と☆に当てはまる数を考えてみよう。

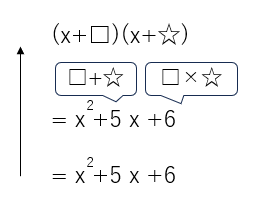
足して「５」、かけて「６」になる数だから、□と☆にはそれぞれ「２」と「３」がはいることがわかるかな？

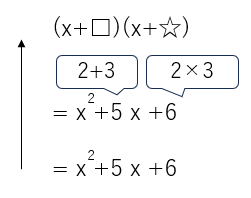
だから、x²+5x+6を因数分解すると、(x+2)(x+3)になるよ。ちなみに(x+3)(x+2)でもOKだよ。

だって、(x+2)(x+3)の間には「×（かける）」が省略されていて、２×３も３×２も同じだからね。

同じような問題をもう一問やってみよう。

x²+4x+3の因数分解

x²+4x+3を(x＋□)(x+☆)の形にできたら因数分解の完成だよ。□と☆に当てはまる数を考えてみよう。

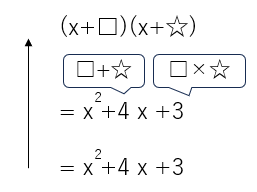
足して「４」、かけて「３」になる数だから、□と☆にはそれぞれ「１」と「３」がはいることがわかるかな？

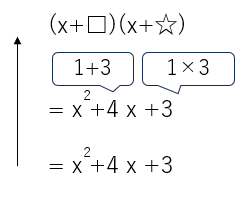
だから、x²+4x+3を因数分解すると、(x+1)(x+3)になるよ。ちなみに(x+3)(x+1)でもOKだよ。

乗法公式を逆に使って因数分解

今まで解いた２問の因数分解は乗法公式１を使った問題だったんだよ。

上の乗法公式は展開するときに使うものだから、因数分解バージョンに直すと下のようになるよね。まあ、左辺と右辺を入れ替えただけだけど。

上の「a」と「b」に当てはまる数を見つけたらOKということだよ。慣れるとすぐに「a」と「b」に当てはまる数が求められるようになるはず！

(1)

x²+3x+2

=x²+(a+b)x+ab

足して「３」、かけて「２」になる数　　→１と２

=x²+(1+2)x+1×2

=(x+1)(x+2)

(2)

x²-8x+12

=x²+(a+b)x+ab

足して「－８」、かけて「１２」になる数　　→　－２と－６

=x²+(-2-6)x-2×(-6)

=(x-2)(x-6)

(3)

x²+4x-12

=x²+(a+b)x+ab

足して「４」、かけて「－１２」になる数　　→　－２と６

=x²+(-2+6)x-2×6

=(x-2)(x+6)

マイナスが入ってくるとaとbの数を見つけるのが一気に難しくなるね。

aとbの数を早く見つけるコツ

慣れるまではaとbの数をなかなか見つけられないと思うんだけど、コツがあるんだ。

コツは「かけて○○になる数を先に考える」。

足して○○に数って無限にあるんだけど、かけて○○になる数は少ないんだ。

だから、「かけて○○になる数」で候補を絞って「足して○○になる数」で１つに決めるのがいいよ。

さっきの

足して「４」、かけて「－１２」になる数　

だったら、「かけて－１２」って下の数だけだよ。

この中で、

「足して４になる数」を見つけたら、速くaとbの数が求められるよね。

因数分解の公式

x²+(a+b)x+abの因数分解

さっきの因数分解１の公式「x²+(a+b)x+ab=(x+a)(x+b)」を知っていれば、ほとんどの問題が因数分解ができちゃうんだよね。

例えば、次のような問題を考えてみよう。

x²+6x+9

=x²+(a+b)x+ab

足して「６」、かけて「９」になる数　　→３と３

=x²+(3+3)x+3×3

=(x+3)(x+3)

=(x+3)²

だから、因数分解１の公式は絶対にマスターしておかないとだめだよ。

x²+2ax+a²の因数分解

因数分解の公式１を使えばどんな問題でも因数分解できるんだけど、次のような問題の時は別の公式を使うともっと速く答えを求められるよ。

x²+6x+9を因数分解しよう。

まず、乗法公式２を思い出してみよう。

公式２のようにx²+6x+9を次のように形を変えてみると

x²+2×3×x+3²

上の式を公式２「x²+2ax+a²」と比べると、「a=3」になっていることがわかるかな。

だから因数分解すると「(x+3)²」になるよ。

x²+8x+16を因数分解しよう。

公式２のようにx²+8x+16を次のように形を変えてみると

x²+2×4×x+4²

上の式を公式２「x²+2ax+a²」と比べると、「a=4」になっていることがわかるかな。

だから因数分解すると「(x+4)²」になるよ。

この公式が使えるかどうかのチェックポイントは２つ

①x²+○ｘ＋△の　△が「何かの数字」を２乗した数になっているか？

→なっていた場合　（ｘ＋何かの数字）^２になる可能性あり

②x²+○ｘ＋△の　○が「何かの数字」の２倍になっているか？

→なっていた場合　（ｘ＋何かの数字）^２と因数分解できる。

x²-2ax+a²の因数分解

x²–8x+16を因数分解しよう。

8xの前がマイナスになっているよ。こういうときは乗法公式３をヒントに考えよう。

公式３のようにx²-8x+16を次のように形を変えてみると

x²-2×4×x+4²

上の式を公式３「x²-2ax+a²」と比べると、「a=4」になっていることがわかるかな。

だから因数分解すると「(x-4)²」になるよ。

この公式が使えるかどうかのチェックポイントはさっきと同じ２つ

①x²－○ｘ＋△の　△が「何かの数字」を２乗した数になっているか？

→なっていた場合　（ｘ－何かの数字）^２になる可能性あり

②x²－○ｘ＋△の　○が「何かの数字」の２倍になっているか？

→なっていた場合　（ｘ－何かの数字）^２と因数分解できる。

x²-a²の因数分解

x²-a²の因数分解はもっとも簡単だよ。

乗法公式４を思い出してみよう。

x²-a²になっていた場合、(x+a)(x-a)と因数分解できることがわかるね。

実際に問題を解いてみよう。

x²-25の因数分解だったら

x²-25

=x²-5²

x²-a²の形になっているから、(x+a)(x-a)と因数分解できるよ。

今回は「a=5」だから

x²-5²

=(x+5)(x-5)

となるよ。

因数分解の公式一覧

因数分解の公式４つをもう一度確認しよう。

特に大事になってくるのは公式１だから、公式１だけは最低限マスターしておくといいよ。

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。