「三角形の相似条件」言い方や合同条件との違い・証明問題例を紹介

中学校３年生の数学で学習する「三角形の相似」について、「相似条件」にはどんなものがあるのか、どうしてそのような条件が成り立つのか、合同条件と相似条件の違いや、相似条件の言い方の注意点などを解説しているよ。

相似条件を使った、相似の証明問題の解き方も紹介しているよ。

「三角形の相似条件」言い方や合同条件との違い・証明問題例を紹介のPDF（19枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

３組の辺の比がすべて等しい

まずひとつめの条件「３組の辺の比がすべて等しい」。

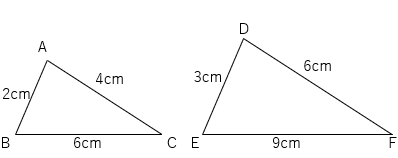
どういうことかというと、２つの三角形があったとき、その２つの三角形同士の辺の比（ひとつは２cmで、もうひとつは４cmだから１：２になっているなど）が、３つの辺すべての組み合わせで同じ比になっている、ということなんだ。

たとえば下の２つの三角形の３組の辺の比はすべて２：３になっているから相似といえるよ。

でもなぜ、３組の辺の比がすべて等しいと、相似ということができるのだろう。

たとえば、次のような三角形を考えてみよう。

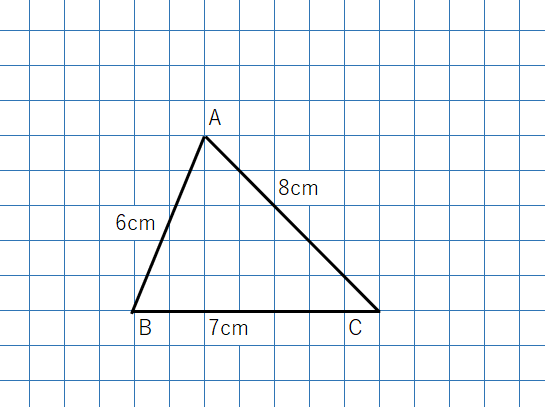
すべての辺の長さを２倍してみよう。すると次のような三角形A’B’C’になるよ。

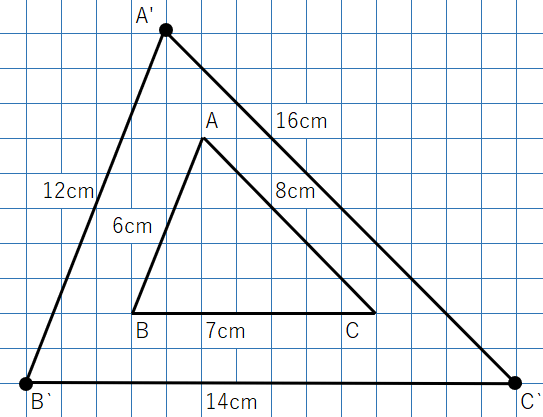
△ABCと△A’B’C’この２つの三角形は相似になるか考えよう。

以前学習した「相似の中心」の考えを使って、相似の中心と対応する点を結ぶと次のようになるよ。

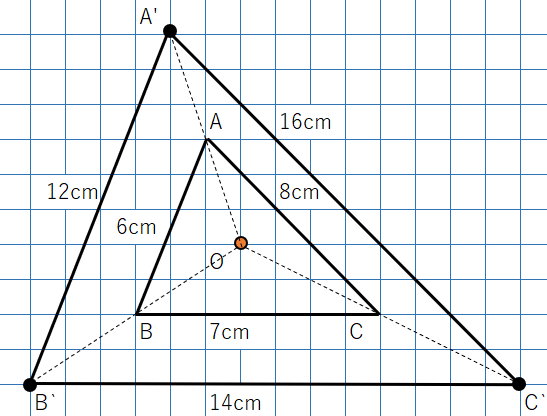
この図をみると、
OA：OA‘＝１：２
OB：OB’＝１：２
OC：OC’＝１：２

になっているから、２つの三角形は「相似の位置にある」といえるよね。
「相似の位置にある」と呼ぶための条件は覚えているかな？

「相似の位置にある」と呼ぶための条件

２つの図形の対応する点を結んだ直線が相似の中心で交わる
相似の中心から対応する点までの距離の比がすべて等しい

２つの図形の対応する「点ABC」と「点A’B’C’」を結んだ直線が相似の中心で交わっているよね。そして、相似の中心から対応する点までの距離の比はすべて1：2で等しいよね。

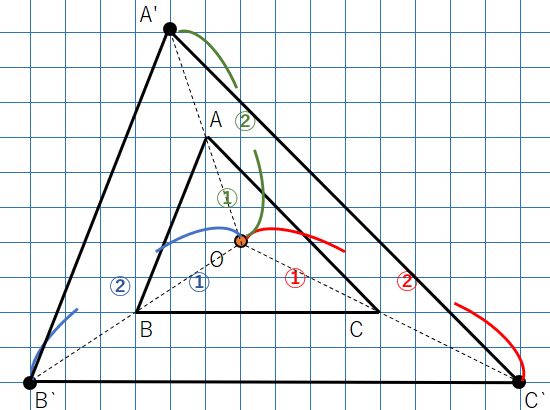
だから、この２つの図形は「相似の位置にある」ね。

「相似の位置にある」ということは、つまり２つの三角形は「相似な図形」ということができるよね。

相似条件➀「３組の辺の比がそれぞれ等しい」

２つの三角形の対応する３組の辺の比が、すべて同じ比になっているということ

【たしかめ】
３つの辺の長さを２倍にする（３組の辺の比が、すべて１：２になる）
→２つの図形の対応する点を結んだ直線が相似の中心で交わる
→２つの図形は相似の位置にある（つまり相似である）

３組の辺の比が全部同じになっていたら、２つの三角形は相似になるってことだね。

２組の辺の比とその間の角がそれぞれ等しい

２つめの条件「２組の辺の比とその間の角がそれぞれ等しい」。

とういうことかというと、２つの三角形があったとき、その２つのあ三角形同士の辺の比が、２組同じで、さらにその２組の辺の間の角度の大きさが同じになっている、ということなんだ。

たとえば下の２つの三角形の２組の辺の比は２：３になっていて、その間の角度は７０°になっているよね。
だからこの２つの三角形は相似といえるよ。

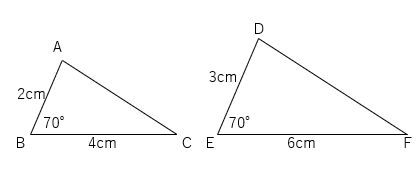
でもなぜ、三角形の２組の辺の比が等しく、その２組の辺の間の角度が同じだと相似であるといえるのだろう。

たとえば、次の三角形を考えてみよう。

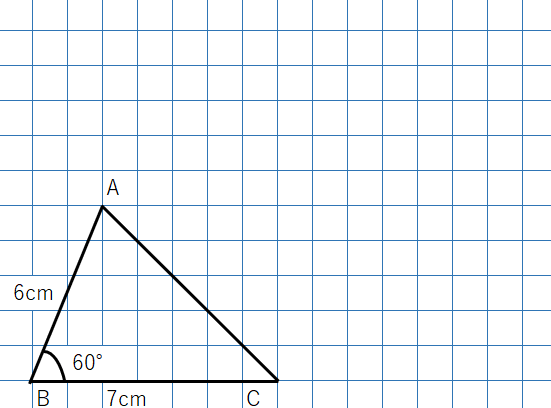
点Bをスタート地点として、この三角形のABとBCの長さを２倍するよ。

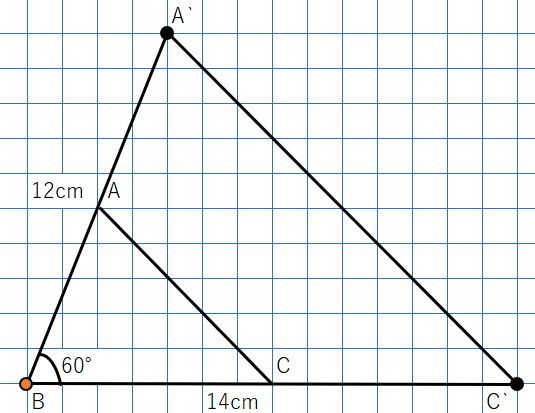
△ABCと△A’BC’、この２つの三角形が相似になるか考えよう。

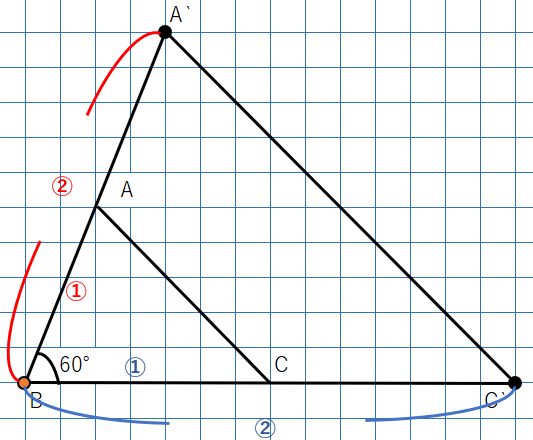
今回は相似の中心が点Bになっているね。
そして
AB：A‘B＝１：２
CB：C’B＝１：２

になっているね

相似の位置にあると呼ぶための条件は、２つの図形の対応する点を結んだ直線が相似の中心で交わることだから、この２つの三角形ABCとA’BC’は「相似の位置にある」といえるよね。つまり「相似な図形」ということができるね。

相似条件②「２組の辺の比とその間の角がそれぞれ等しい」

２つの三角形の対応する２組の辺の比が、同じ比になっていて、その２組の辺の間にある角の大きさがそれぞれ同じということ

【たしかめ】
１つの頂点をもとに、その両側の２つの辺の長さを２倍にする（２組の辺の比が、どちらも１：２になる）
→２つの図形の対応する点を結んだ直線が相似の中心（もとにした頂点）で交わる
→２つの図形は相似の位置にある（つまり相似である）

この条件で注意するのは、「２組の間の角度が」等しくなるということが必要だという事。

なぜなら、２組の間の角度が相似の中心になっているからだね。

２組の角がそれぞれ等しい

３つめの条件は「２組の角がそれぞれ等しい」。

どういうことかというと、２つの三角形があったとき、その２つの三角形同士の角が２つ大きさが一緒であれば、その２つの三角形は「相似な図形」ということができるんだ。

たとえば下の２つの三角形を見てみよう。
２つの角度（７０°と２０°）がそれぞれ同じで、相似になっているよ。

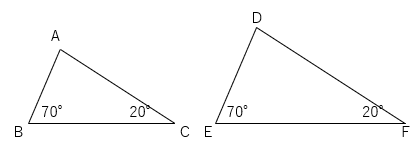
でもなぜ、２組の角の大きさが同じだと、相似といえるのだろう。

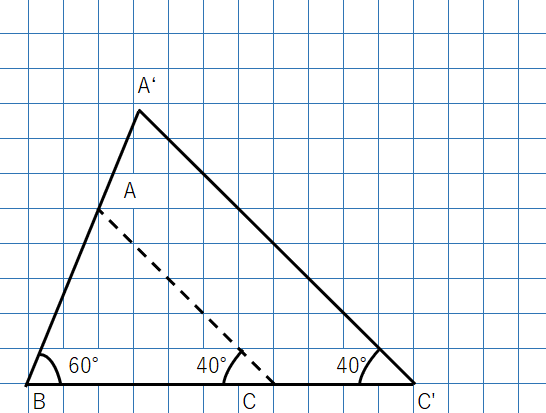
たとえば、下の図のように、２つの角が４０°と６０°の三角形で考えてみよう。

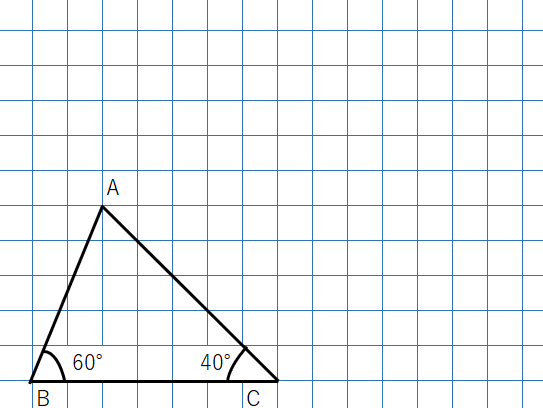
角度を変えずに辺の長さを変えてみると次のようになるよ。

↓

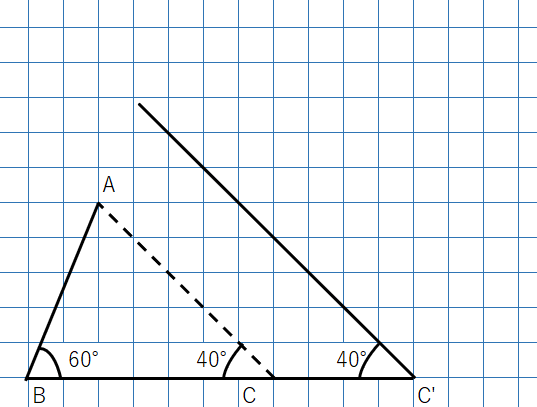
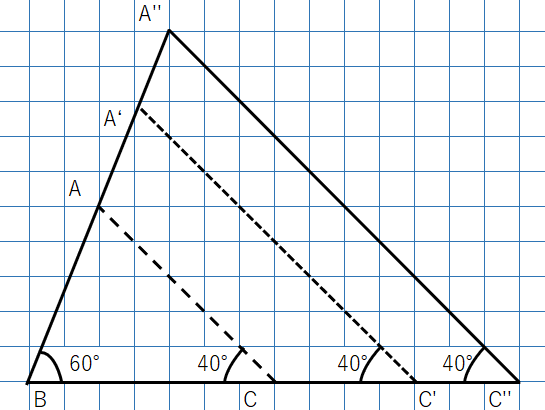
２つの角度が同じ三角形を３つ書いたけど、すべて相似であることがわかるかな。

なぜならAもA’もA”も角度は

１８０°－（６０°＋４０°）＝８０°になって

３つの角度が同じになるよね。

三角形は、３つの角度が同じであれば形が変わらないので、「相似」だといえるよ。

相似条件③「２組の角がそれぞれ等しい」

２つの三角形の対応する２組の角が、それぞれ同じ大きさになっているということ

【たしかめ】
２つの角の大きさがきまれば、のこりの１つの角の大きさも決まる
→２角が同じということは、つまり３角が同じということ
→３角が同じ三角形は、同じ形になる（つまり相似である）

この「２組の角がそれぞれ等しい」という条件はよく問題になって出てくるよ。

合同条件と相似条件の違いに着目してみよう

今回学習した「相似条件」と、２年生の数学で学習した「合同条件」は、なんだかとても似ているね。

相似条件を新たに学習したことで、これらがごちゃ混ぜになってしまって、混乱してしまう子もいるかもしれないね。

ここで、「合同条件」と「相似条件」の違いをはっきりしておこう。

着目しているポイント	合同条件	相似条件
３組の〇〇が等しい	３組の辺がそれぞれ等しい	３組の辺の比がすべて等しい
２辺と１角に着目	２組の辺とその間の角がそれぞれ等しい	２組の辺の比とその間の角がそれぞれ等しい
２つの角に着目	１組の辺とその両端の角がそれぞれ等しい	２組の角がそれぞれ等しい

表にまとめてみると、合同条件と相似条件がとても似ていることがさらによく分かるね。

どちらも条件は３つ。
さらに、着目しているポイントも同じなんだ。

３組の〇〇が等しい

「合同条件」と「相似条件」どちらも、２つの三角形の、３組の「なにか」が等しいというのがポイントになっているところが同じだね。

あとは、それが合同条件の場合は「辺」で、相似条件の場合は「辺の比」となっているところが違う部分だね。

「合同」は２つの三角形がぴったり重ならなくてはならないから、「辺」そのものが同じでなくてはいけない。
それに対して、「相似」は同じ形であればいいので、「辺の比」が同じであればいいということだね。

２辺と１角に着目

これも、「合同条件」と「相似条件」どちらも、２組の辺とその間の角に着目しているところが同じだね。

あとはやっぱりそれが合同条件の場合は「辺」で、相似条件の場合は「辺の比」となっているところが違う部分だね。

２つの角に着目

この条件のポイントは、合同と相似でははっきり違うところがあるね。

それは、合同条件では２角の間の辺も等しくなくてはいけないけれど、相似条件では２角だけが同じであれば、辺のことは気にしなくてよいというところ。

どうしてかというと、三角形は、２角が決まれば自動的に残りの１角も大きさが決まるよね。なぜなら、内角の和は180°と決まっているからだね。

つまり、２角が同じであれば、それは「３角とも等しい」ということになるんだ。

そして、三角形は、３つの角の大きさが決まっていると、出来上がる形はたったひとつなんだよ。
つまり、３角とも等しければ、２つの三角形は同じ形になる（相似になる）というわけなんだ。

だから、相似条件の場合は、「２角が等しい」だけでOKなんだね。

相似条件の言い方について

相似条件の言い方は、これまでに説明したとおり

３組の辺の比がすべて等しい
２組の辺の比とその間の角がそれぞれ等しい
２組の角がそれぞれ等しい

という言い方だね。

少し長くて覚えづらいかもしれないけれど、証明問題で相似条件を使うときは、この言い方どおりに書く必要があるので、頑張って覚えよう！

相似条件の言い方についての補足

相似条件の言い方には、以下のように別の言い方もあるよ。

「３組の辺の比がすべて等しい」
→三辺比相等（さんぺんひそうとう）
「２組の辺の比とその間の角がそれぞれ等しい」
→二辺比挟角相等（にへんひきょうかくそうとう）
「２組の角がそれぞれ等しい」
→二角相等（にかくそうとう）

けれど、これらは現在、教科書では使われていないんだ。
テストや試験などでは、この言い方で答えると減点されてしまう場合もあるとのことなので、注意しよう。

相似な三角形の証明問題に挑戦しよう

テストでは、相似条件を使って２つの三角形が相似であることを証明する問題が出ることもあるよ。
どんな問題が出てくるのか、どうやって証明をすればよいのか紹介するよ。

相似の証明問題１

図の△ABCは∠BAC＝９０°の直角三角形である。頂点Aから辺BCに垂線を下ろしその交点をDとする。

△ABC∽△DBAを証明しなさい。

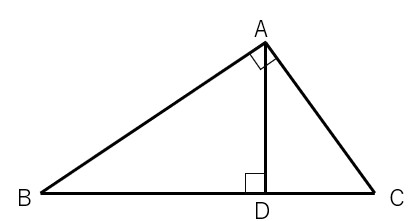
まず、三角形△ABCと△DBAに分けて考えよう。

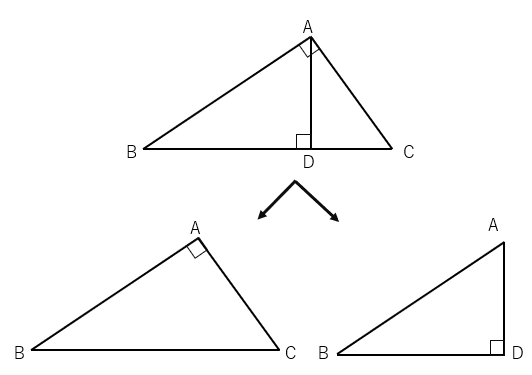
左と右の三角形で角度が同じところがあるよね。

∠Bは２つに分ける前には重なっているから等しくなるよね。（合同で学習した「共通」）

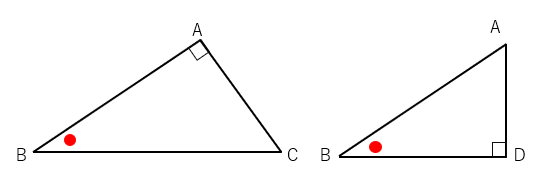
△ABCと△DBAを見ると、「赤丸の角度」と「直角」が等しいから

相似条件「２組の角がそれぞれ等しい」をクリアするね。相似条件をクリアしたから２つの三角形は相似になることがわかるね。

きちんとした文章で証明すると次のようになるよ。

△ABCと△DBAにおいて

仮定より　∠BAC=∠BDA=９０°　　　・・・①

共通な角は等しいので　∠B＝∠B　　・・・②　←「∠Bは共通」　でもOK

①②より、２組の角がそれぞれ等しいから

△ABC∽△DBA

相似の証明問題２

下の図で△AOD∽△COBを証明しなさい。

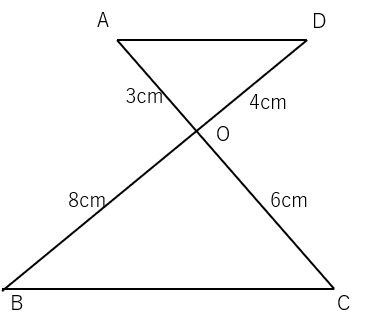
対頂角は等しいから赤丸の部分の角の大きさが等しくなるよね。

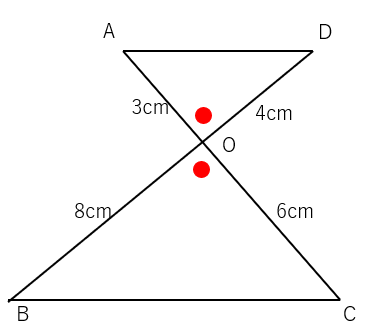
△AODと△COBを分けて考えよう。

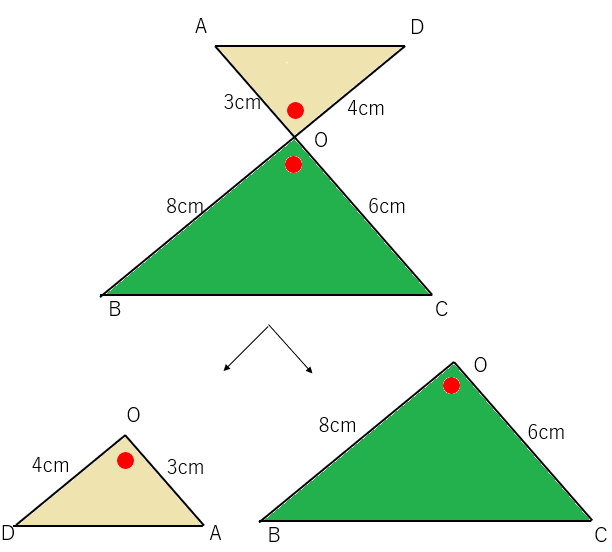
※△AODは△OBCに向きを合わせて回転させているよ。

対応する辺の比を考えよう

AO：CO＝３：６＝１：２

DO：BO＝４：８＝１：２

２組の辺の比が１：２になっていることがわかるね。

さらに、２組の辺の間の角が等しいよね。

なので、三角形の相似条件「２組の辺の比とその間の角がそれぞれ等しい」をクリアしているので、「相似な図形」であるということがわかるね。

きちんとした文章で証明すると次のようになるよ。

△AOD と△COBについて

仮定から、

AO：CO ＝３ : ６ = １ : ２　　　・・・①

DO：BO = ４: ８ = １：２　　・・・ ②

対頂角は等しいので、

∠AOD = ∠COB・・・ ③

①②③より、

２組の辺の比とその間の角がそれぞれ等しいので、

△AOD ∽ △COB