三平方の定理を利用した応用問題の頻出3パターンの解き方を解説
中学3年生の数学で学習する「三平方の定理を利用した応用問題」について、定期テストや入試問題で頻出の「円の中の線分の長さを求める問題」「直方体の対角線の長さを求める問題」「錐の体積を求める問題」の3パターンの解き方をわかりやすく解説するよ。
円の中の線分の長さを求める問題(平面図形)
まずは平面図形の問題。
円の中に弦ABなどがあって、半径と、中心から弦に対しての垂線が引くことで直角三角形を作ることができるパターンだよ。
問題によって、「半径を求める」「垂線の長さを求める」「弦ABの長さを求める」など変わるけれど、結局は半径・弦・垂線の3つで直角三角形をつくることができれば、あとは三平方の定理を利用して解けば大丈夫。
それでは実際に問題を確認してみよう。
次の図の円Oは半径が5cmで、弦ABの長さが8cmである。
中心Oから弦ABに引いた垂線の長さを求めなさい。
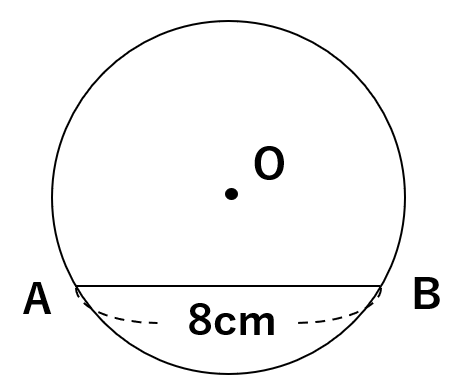
まず、わかる長さと求めたい長さを図に書いてみよう。
ポイントは半径をどのように書くか。次のように半径を描いてしまったら、この問題は解けないよ。
【ダメな半径の描き方】→このように描くと答えを求められないよ。
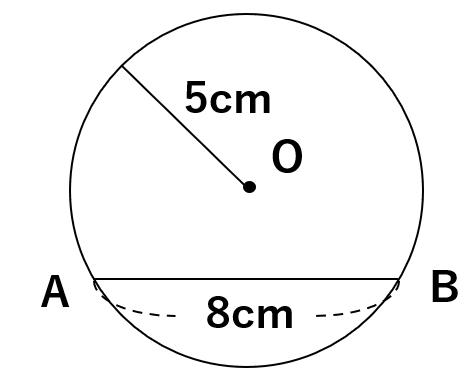
なぜなら、三平方の定理を使った解くことを考えたら、「直角三角形」を作らなくちゃいけないからだね。
だから半径は次のように描くといいよ。
【正しい半径の描き方】→このように描くと答えを求められるよ。
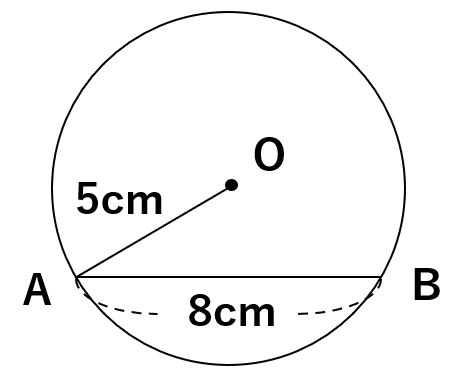
中心Oから弦ABへの垂線は次のようになって、直角三角形OAHができあがったね。AHの長さは弦ABの半分になるよ。
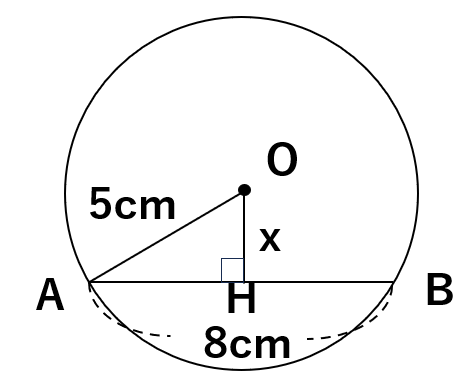
なぜなら、OからBに半径を描いた場合、三角形OABは二等辺三角形になるね(OAもOBも半径で同じ5cmだから)。
ということは、二等辺三角形の頂点から底辺に引く垂線は、底辺を垂直に二等分するという定理が使えるんだ。
だから、中心Oから弦ABに引いた垂線は、弦ABを垂直に二等分するよ。
こうして、斜辺が5cm、1辺が4cmの直角三角形OAHが出来上がったね。
これで三平方の定理が使えるようになったよ。
三角形OAHで三平方の定理を使うと、
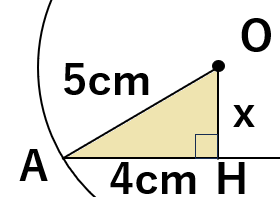
a2+b2=c2
42+x2=52
16+x2=25
x2=25-16
x2=9
x=±3
長さにマイナスはありえないから、OHの長さは3cmと求めることができるよ。
ちなみに「直角三角形の比の7パターン」のうち、「3:4:5の比」を覚えていたら、いちいち三平方の定理を使わなくてもよかったね。
このようにとても便利な比の7パターンは、ぜひ覚えておくといいね。
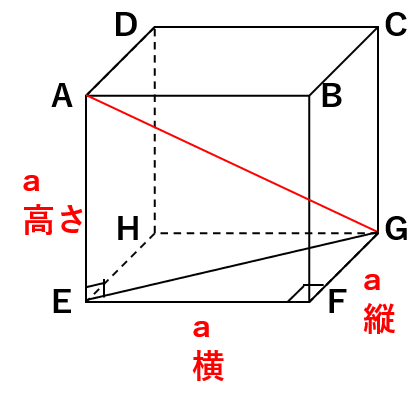
直方体の対角線の長さを求める問題(空間図形)
空間図形である直方体の対角線も、三平方の定理で求めることができるんだ。
これから直方体の対角線を三平方の定理で求める方法をくわしく解説するけれど、直方体の対角線は次のような公式で求めることもできるんだ。
まずはその公式を紹介するよ。
すごく大事な公式だからしっかり覚えよう。
直方体の対角線の長さ
AG=\(\sqrt{a^2+b^2+c^2}\)
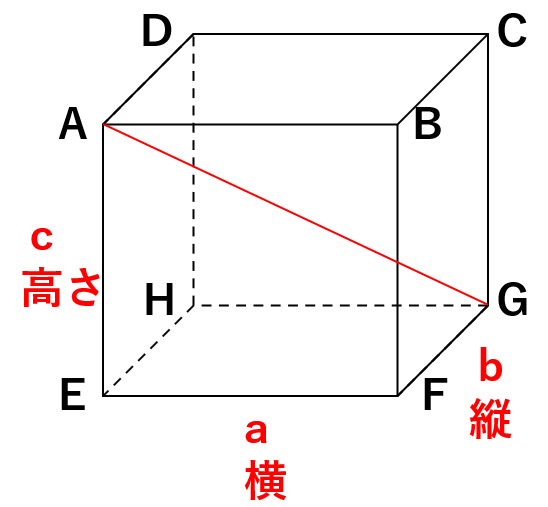
直方体の高さ・横・縦の3辺の長さをそれぞれ2乗したものを足して、ルートをつけたものが対角線の長さになるってことだね。
では、なぜ、AG=\(\sqrt{a^2+b^2+c^2}\)と表すことができるのかを考えてみよう。
① EGの長さを求めよう
点E、Gを結ぶと、△EFGは直角三角形になるよね。
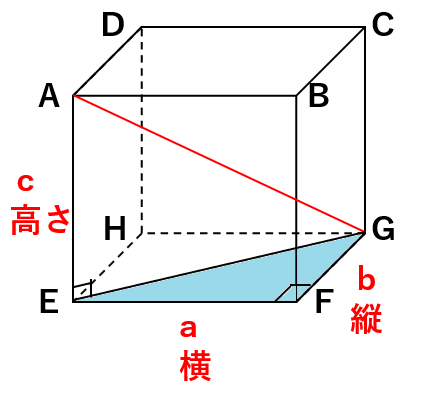
△EFGで三平方の定理を使うと
EG2=a2+b2
になるよね。
あえてこれ以上計算しないで、ひとまず置いておくよ。
② AGの長さを求めよう
△AEGも直角三角形になるよね。
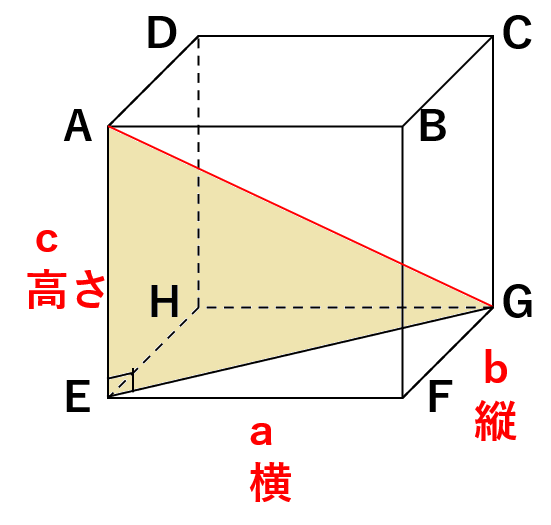
△AEGで三平方の定理を使うと
AG2=EG2+AE2
になるよね。
EG2はさっき求めた結果、「a2+b2」と表すことができるね。
AE2は、高さのことだから、「c2」と表すことができるので、それぞれを代入すると次のようになるよ。
AG2=EG2+AE2
↓
AG2=a2+b2+c2
なので、対角線AGの長さは
AG=\(\sqrt{a^2+b^2+c^2}\)
になるよね。
直方体の対角線の長さ
AG=\(\sqrt{a^2+b^2+c^2}\)

今回は直方体で考えたけれど、
これがもし立方体だったら、すべての辺の長さが同じだから次のようになるよ。
立方体の対角線の長さ
立方体の1辺の長さをaとすると、さっきのAG=\(\sqrt{a^2+b^2+c^2}\)のbとcをaに置き換えることができるね。
AG=\(\sqrt{a^2+a^2+a^2}\)
AG=\(\sqrt{3a^2}\)
AG=\(\sqrt{3}\)×\(\sqrt{a}\)×\(\sqrt{a}\)
AG=\(\sqrt{3}\)a
直方体の対角線の長さの求め方を覚えてしまえば、立方体だって簡単に求めることができるようになるね。
錐の体積を求める問題(空間図形)
最後のパターンは、空間図形の「錐」の体積を求める問題。
「円錐・角錐」どちらでも考え方は同じだよ。
錐の体積は(底面積)×(高さ)×\(\frac{1}{3}\)で求めることができるよね。
まずはその「底面積」または「高さ」を、三平方の定理を使って求めることがポイントなんだ。
今回は、正四角錐の場合として解説するね。
下の図のような、底面の1辺が4cmの正方形で、他の辺の長さがすべて8cmの正四角錐OABCDの体積を求めなさい。
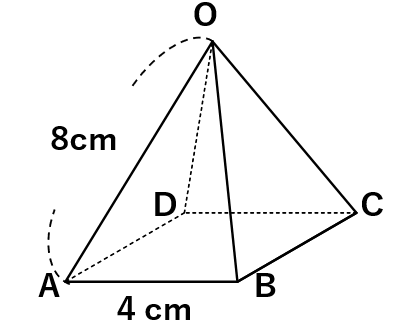
四角錐の体積は(底面積)×(高さ)×\(\frac{1}{3}\)で求まるんだったよね。底面が正方形だから、底面積は簡単に計算できるけど、高さがわからないね。
高さを求めよう
高さを求めるために、頂点Oから底面への垂線OHを引こう。
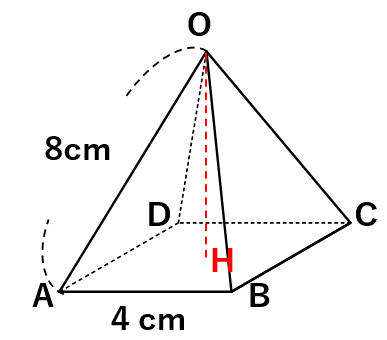
これだけじゃ高さOHを求めることができないから、正方形ABCDの対角線を引いてみよう。
そうすると2つの対角線は点Hで交わってAC⊥OH、BD⊥OHになるよ。
なぜなら、1年生でも勉強したけれど、
頂点Oから底面に垂線OHを引いたとき、OHと面ABCDが垂直になるならば、
面ABCD上にある辺はすべてOHと垂直になるからだよ。
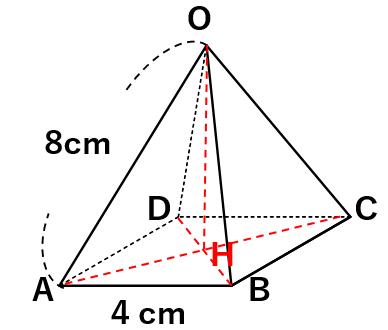
AHの長さを求めよう
正方形ABCDに注目してAHの長さを求めよう。
この立体を上から見たら次のようになるよね。
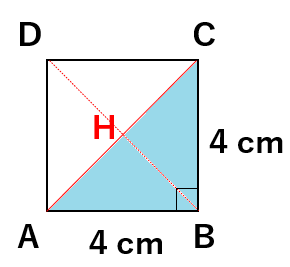
対角線ACの長さは三平方の定理を使うと
AC2=AB2+BC2
AC2=42+42
AC2=16+16
AC2=32
AC=±\(\sqrt{32}\)
AC=±4\(\sqrt{2}\)
ACの長さは4\(\sqrt{2}\)だということがわかったね。
求めたかったAHはACの半分だから、
AH=4\(\sqrt{2}\)÷2
AH=2\(\sqrt{2}\)
になるね。
OHの長さを求めよう
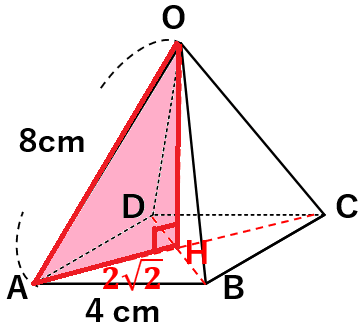
△OAHも直角三角形になるから、三平方の定理を使うと
AH2+OH2=OA2
(2\(\sqrt{2}\))2+OH2=82
8+OH2=64
OH2=64-8
OH2=56
OH=±\(\sqrt{56}\)
OH=±2\(\sqrt{14}\)
高さOHが2\(\sqrt{14}\)と求まったから、いよいよ体積を求めていこう。
体積を求めよう
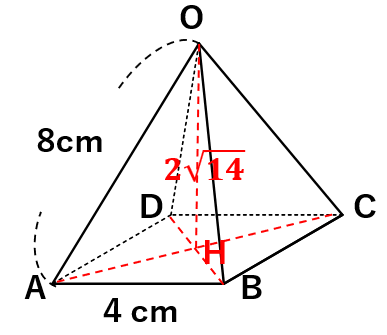
四角錐の体積は
(底面積)×(高さ)×\(\frac{1}{3}\)
で求まるから、
4×4×2\(\sqrt{14}\)×\(\frac{1}{3}\)
=\(\frac{32\sqrt{14}}{3}\)
体積は\(\frac{32\sqrt{14}}{3}\)cm3と求めることができたね。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。


