「相似な図形の面積比」相似な三角形・多角形・円の相似比と面積比

中学３年生の数学で学習する「相似な図形の面積比」について、相似な図形の相似比と面積比の関係について、三角形の場合、多角形の場合、そして円の場合をそれぞれくわしく解説するよ。

相似な図形の相似比と面積比の定理について学習しよう。

「相似な図形の面積比」 相似な三角形・多角形・円の相似比と面積比のPDF（17枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 相似な三角形の相似比と面積比を調べてみよう
• 相似な多角形の相似比と面積比を調べてみよう
• 相似な平面図形の周と面積の定理
• 相似な図形の面積比の定理を使った問題
• まとめ

相似な三角形の相似比と面積比を調べてみよう

相似な図形の性質の解説ページでは、三角形の相似比について学習したね。
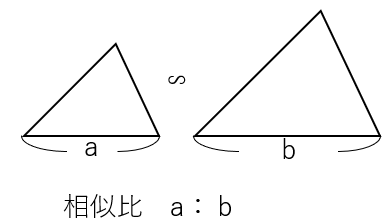
下の図のような２つの三角形が相似だった場合、対応する辺の比のことを相似比って呼んだよね。

下の図の場合だとａ：ｂが相似比だね。

今回は、「相似な三角形」の「面積の比はどうなっているのか？」について考えてみるよ。

まずは結論を伝えてしまうね。
相似な三角形の相似比と面積比の関係は下の通りになっているよ。

相似な三角形の相似比と面積比

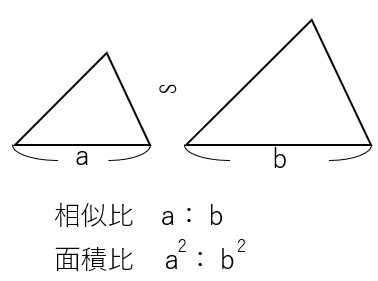
相似な三角形の相似比がａ：ｂであれば、
面積の比（面積比）はａ^２：ｂ^２となる。

面積比がａ^２：ｂ^２になる理由を考える前に、まずは問題を解いてみよう。

相似な三角形の相似比と面積比の問題

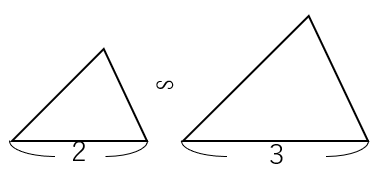
下の２つの三角形は相似で、相似比は２：３になっている。
２つの三角形の面積比を求めなさい。

相似比がａ：ｂのとき、面積比はａ^２：ｂ^２になるから、
相似比が２：３のとき、面積比は２^２：３^２＝４：９になるよ。

下の２つの三角形は相似で、左側の三角形の面積は８cm²である。
右の三角形の面積を求めなさい。

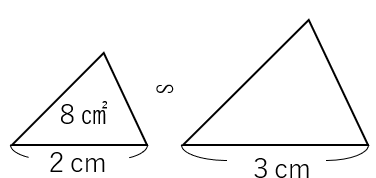
相似比は２：３だから、面積比は２^２：３^２＝４：９になるよね。
右の三角形の面積をｘcm²とすると、次の比例式が作れるよ。

４：９＝８：ｘ

この比例式を解いてｘを求めてみよう。

４：９＝８：ｘ　　比例式の性質ａ：ｂ＝ｃ：ｄならば、ａｄ＝ｂｃを使おう
４×ｘ＝９×８
４ｘ＝７２
ｘ＝１８

右側の三角形の面積は１８cm²と求めることができたね。

なんとなく、面積比の使い方がわかったかな？
じゃあ、相似比がａ：ｂのとき、なぜ面積比はａ^２：ｂ^２になるのか、理由を説明していくね。

相似な三角形の相似比と面積比の関係

次のような、２つの相似な三角形を考えよう。
２つの三角形の相似比が１：２のとき、面積比「？」がどうなるかをSTEP１～４の順で考えよう。

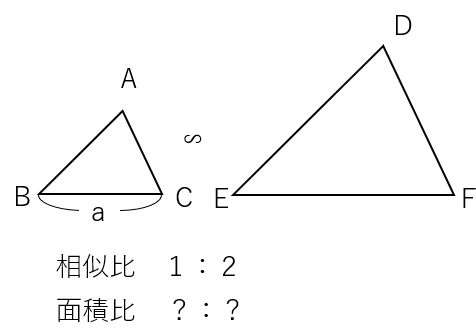
STEP1　底辺の長さを求めよう

相似比が１：２なのだから、△ABCの長さを２倍すると、△DEFの長さになるということだね。

ということは、BCの長さがａだとすると、EFの長さはａ×２＝２ａだよね。

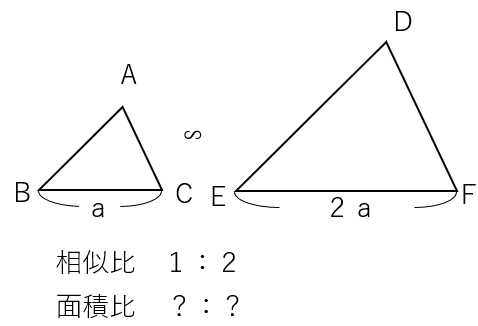
STEP２　高さを求めよう。

△ABCの高さをｈとして考えよう。
※高さは英語で「height（ハイト）」なので、数学ではアルファベットの「ｈ」を使うことが多いよ。

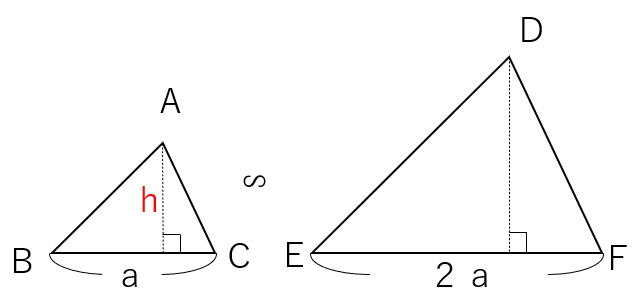
相似比が１：２なので、△ABCの高さを２倍したら△DEFの高さになるよね。

だから△DEFの高さはｈ×２＝２ｈになるよ。

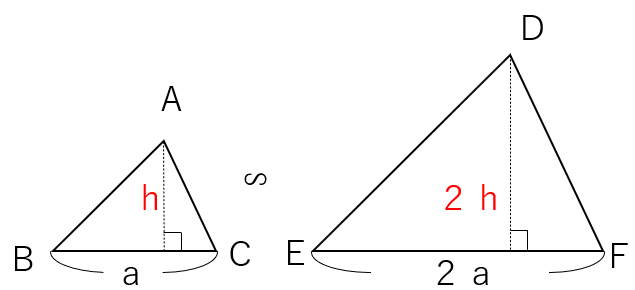
STEP３　面積を求めよう。

三角形の面積は（底辺）×（高さ）÷２で求まるから

・△ABCの面積＝ａ×ｈ÷２＝\(\frac{ａｈ}{２}\)

・△DEFの面積＝２ａ×２ｈ÷２＝２ａｈ

STEP４　面積比を求めよう。

まとめると
△ABCの面積：△DEFの面積＝\(\frac{ａｈ}{２}\)：２ａｈ

もう少し簡単にするために、両方を２倍してみると

△ABCの面積：△DEFの面積
＝\(\frac{ａｈ}{２}\)：２ａｈ
＝\(\frac{ａｈ}{２}\)×２：２ａｈ×２
＝ａｈ：４ａｈ

両方をａｈで割ってみよう。

ａｈ：４ａｈ
＝ａｈ÷ａｈ：４ａｈ÷ａｈ
＝１：４

△ABCの面積：△DEFの面積＝１：４になることがわかったね。

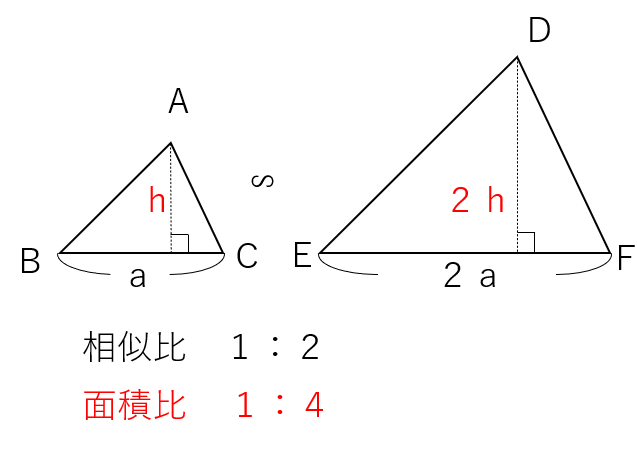
相似比が１：２だったら、面積比は１：４になることがわかったね。
「１：４」は「１^２：２^２」と表すことができるから、次のとおり説明できるんだ。

相似な三角形の相似比と面積比

相似な三角形の相似比がａ：ｂであれば、
面積の比（面積比）はａ^２：ｂ^２となる
=相似比の二乗が面積比になる

相似な多角形の相似比と面積比を調べてみよう

相似な三角形の相似比と面積比の関係についてわかったよね。

次は、三角形以外の多角形ではどうなるかを調べてみよう。
結論は下の通りで、三角形と全く同じになるよ。

相似な多角形の相似比と面積比の関係

相似な多角形の相似比がａ：ｂのとき、なぜ面積の比（面積比）はａ^２：ｂ^２となるのか、確認していくよ。

多角形の例として、次のような相似な五角形を考えてみよう。

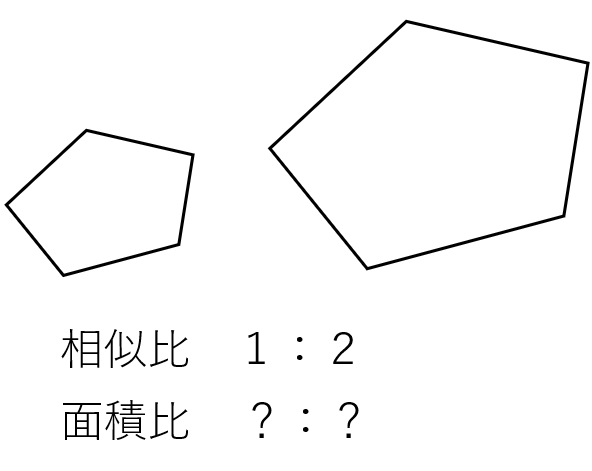
さっき「三角形の相似比と面積比」を確認したので、五角形を次のように三角形にわけて考えてみよう。

２つの五角形は相似だから、同じ色の三角形同士も相似になるよ。

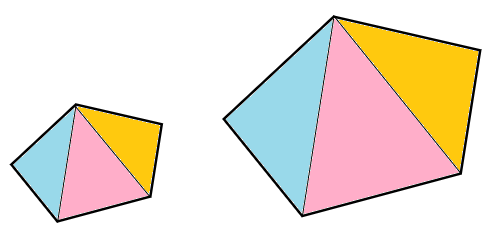
２つの五角形の相似比は１：２ということは、すべての辺の比が１：２になっているということだよね。

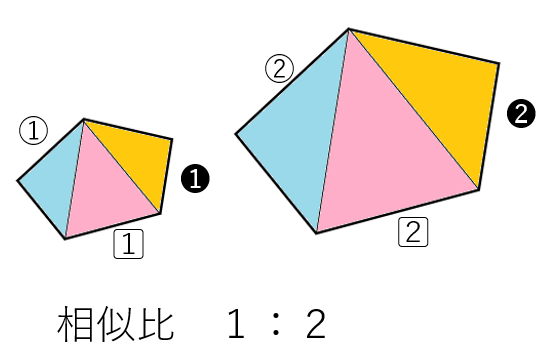
ここで、さっき確認した「相似な三角形の相似比と面積比」の性質を使おう。

五角形の中にある三角形の相似比は１：２だから、面積比は１：４になるよね。

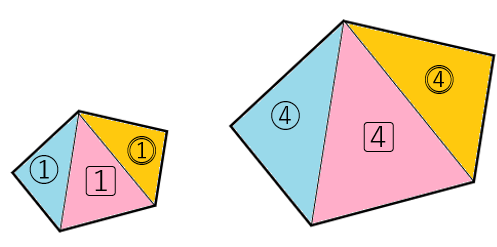
左の三角形の面積をP、Q、Rとしたら、右の三角形の面積はP×４＝４P、Q×４＝４Q、R×４＝４Rになるよね。

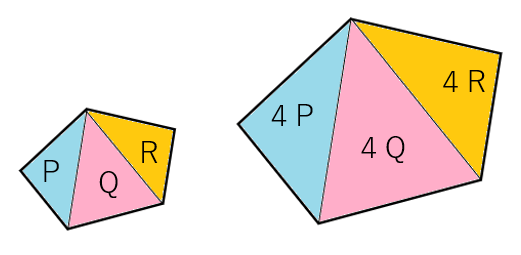
・左の五角形の面積＝P＋Q＋R

・右の五角形の面積＝４P＋４Q＋４R

ということは、左側の五角形の面積の４倍が右の五角形の面積になっているってことだよね。
※4P＋4Q＋4R=4(P＋Q＋R)だよね

つまり、五角形の面積比は１：４になるんだ。

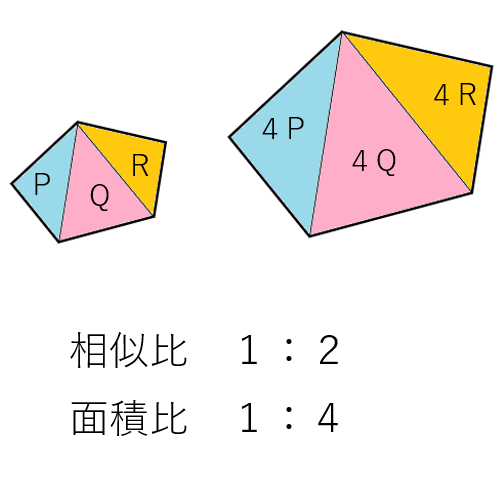
相似比が１：２であれば、面積比が１：４になることがわかったね。
「１：４」は「１^２：２^２」と表すことができるから、次のことが説明できるね。

三角形だけではなくて、多角形でも「相似比の二乗が面積比」になっているんだね。

相似な平面図形の周と面積の定理

今までわかったことは次の通りだよ。

今までは「〇〇角形」という角がある図形の面積比を考えてきたね。
では、最後に円の相似比と面積比の関係について考えていこう。

相似な円の相似比と面積比の関係

結論からいうと、円の相似比と面積比の関係は次のようになるよ。

円の相似比と面積比の関係

• 相似な円の相似比がａ：ｂであれば、
  面積比はａ^２：ｂ^２となる。

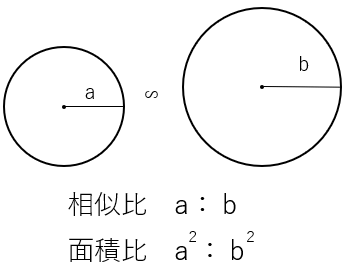
なぜ、面積比はａ^２：ｂ^２になるのかを次の円で考えて確かめてみよう。

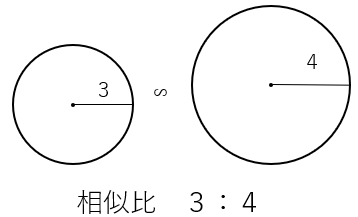
円の面積は（半径）×（半径）×（円周率）で求まるから

・左の円の面積＝３×３×π＝９π

・右の円の面積＝４×４×π＝１６π

まとめると
左の円の面積：右の円の面積＝９π：１６π

もう少し簡単にするために、両方をπでわってみると

左の円の面積：右の円の面積
＝９π：１６π
＝９π÷π：１６π÷π
＝９：１６

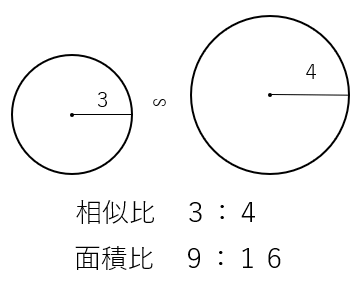
相似比が３：４だったら、面積比が９：１６になることがわかったね。
「９：１６」は「３^２：４^２」と表すことができるから、次のことが説明できるね。

円の相似比と面積比の関係

• 相似な円の相似比がａ：ｂであれば、面積比はａ^２：ｂ^２となる。

円の場合も、相似比の二乗が面積比になることがわかったね。

では、円つながりで、今度は相似比と周の長さの関係についても調べてみよう。

相似な円の相似比と周の長さの関係

次の２つの相似な円の周の長さを求めよう。

円の周の長さは、（直径）×（円周率）で求まるから

・左の円の円周＝６×π＝６π

・右の円の円周＝８×π＝８π

まとめると
左の円の円周：右の円の円周＝６π：８π

もう少し簡単にするために、両方をπでわってみると

左の円の円周：右の円の円周
＝６π：８π
＝６π÷π：８π÷π
＝６：８

両方とも２で割って、左の円の円周：右の円の円周＝３：４と求めることができたね。

相似比が３：４の場合、円周の比も同じになるよ。

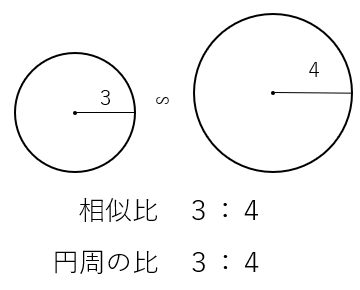
円周の場合は、その比は相似比と同じになるんだね！

相似な平面図形の周と面積の定理

今まで学習してきたことは次の通り。

三角形でも多角形でも円でも、相似比の二乗が面積比になっているから、どんな平面図形でも、相似比の二乗が面積比になることがわかるね。

それと、周の比は相似比と同じになるってことが導けたね。

まとめると次のようになるよ。これはとても大切な知識だからしっかり覚えておこう。

相似な図形の面積比の定理を使った問題

２つのピザは全く同じ形ということは、「相似」だよね。相似比は半径の比だから、２０：３０＝２：３になるよ。

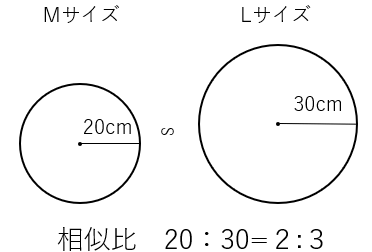
平面図形の面積比は、相似比の二乗になるから

２つのピザの面積比は２^２：３^２＝４：９だね。

４：９ってことは、

Lサイズの面積（９）はMサイズの面積（４）の２倍以上あるから、Lサイズの方がお得ということがわかるよ。

問題

下の図で、四角形ABCD∽四角形EFGHである。

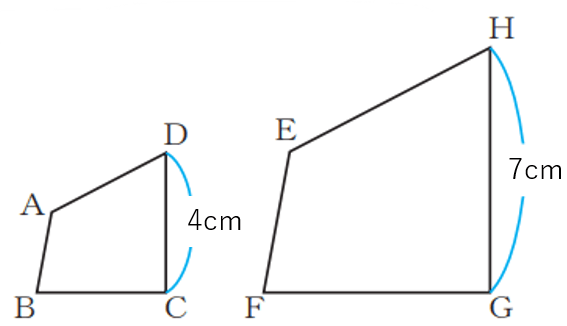
(1) 四角形ABCDの周の長さが１６cmだったとき、四角形EFGHの周の長さを求めよ。

(2) 四角形ABCDの面積が１６cm²だったとき、四角形EFGHの面積を求めよ。

(1)

相似比は４：７だから、周の長さの比も４：７になるよね。

今回求めたい四角形EFGHの周の長さをｘcmとすると次の比例式が成り立つよ。

４：７＝１６：ｘ
４ｘ＝７×１６
４ｘ＝１１２
ｘ＝２８

四角形EFGHの周の長さが２８cmと求まったね。

(2)

相似比は４：７だから、面積比は４^２：７^２＝１６：４９になるよね。

今回求めたい四角形EFGHの面積をｘcm²とすると次の比例式が成り立つよ。

１６：４９＝１６：ｘ
１６ｘ＝４９×１６

両辺１６で割ると、計算が簡単にできるよ。

１６ｘ＝４９×１６
１６ｘ÷１６＝４９×１６÷１６
ｘ＝４９

四角形EFGHの面積が４９cm²と求まったね。

「相似な図形の面積比」まとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。