円周角とは?「円周角の定理」を例題を使ってわかりやすく解説
中学3年生の数学で学習する「円周角の定理」について、円周角とはなにか、円周角とその弧に対する中心角の関係など、円周角の定理をわかりやすく解説するよ。
円周角の定理を使った問題の解き方や、「中心を通らない」円周角のパターンの問題の解き方をくわしく紹介しているよ。
円周角とは
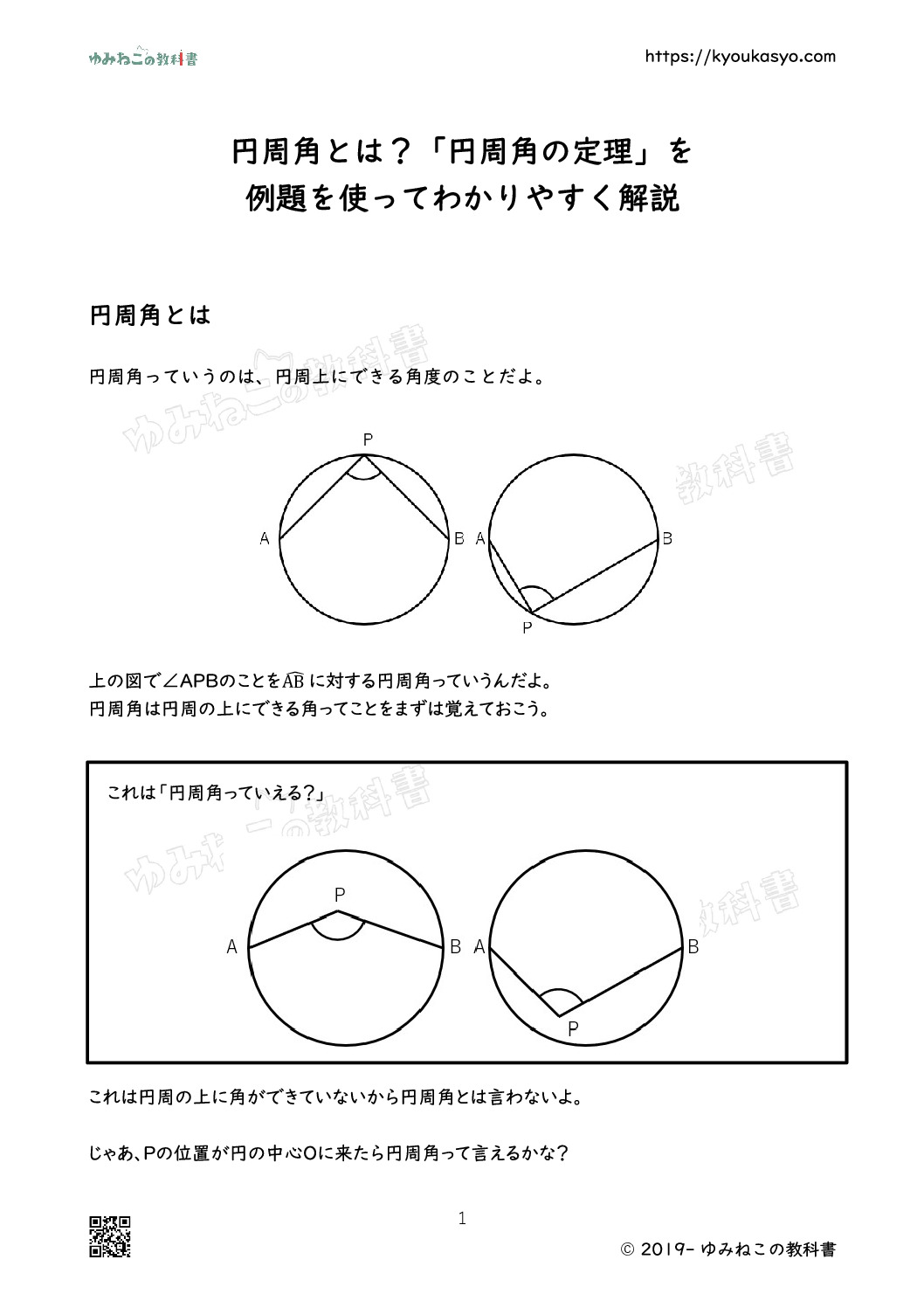
円周角っていうのは、円周上にできる角度のことだよ。
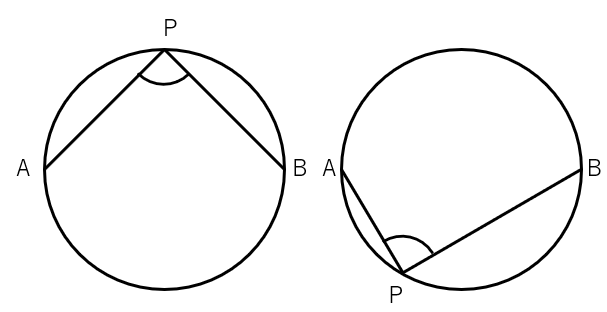
上の図で∠APBのことを\(\overset{\frown}{AB}\) に対する円周角っていうんだよ。
円周角は円周の上にできる角ってことをまずは覚えておこう。
これは「円周角っていえる?」
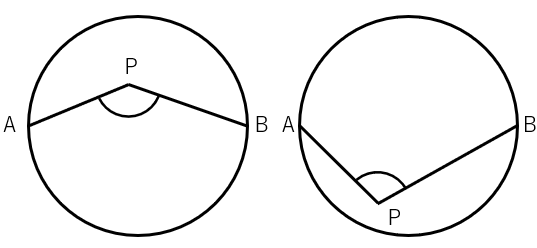
これは円周の上に角ができていないから円周角とは言わないよ。
じゃあ、Pの位置が円の中心Oに来たら円周角って言えるかな?
これは「円周角っていえる?」
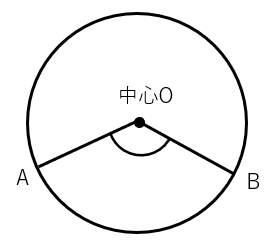
これは中心に角ができているよね。このときの∠AOBのことを中心角って呼ぶよ。
1年生の時に勉強したと思うけど、3年生でも大事になるからね。
1つの弧に対する円周角の大きさ
円周角とは何かがわかったところで、ここからが本題だよ。
円周角には大切な性質があるんだ。
下の図のように、円周上に点Aと点Bを取ろう。
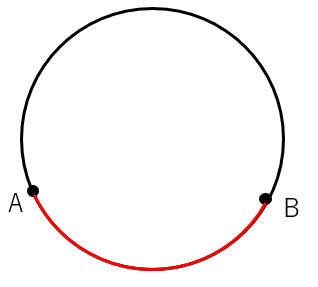
\(\overset{\frown}{AB}\) に対する円周角をたくさん書いてみると「ある性質」が見えてこないかな?
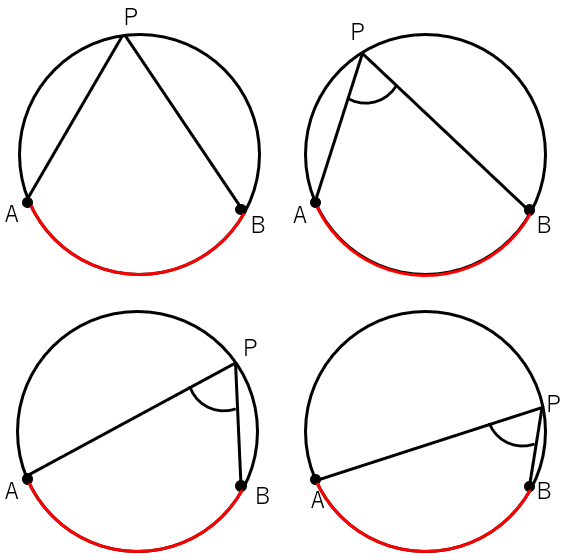
\(\overset{\frown}{AB}\) に対する円周角∠APBの大きさがすべて一定(同じ)になっているよね。
まとめると円周角には次のような性質があるんだ。
円周角の定理①
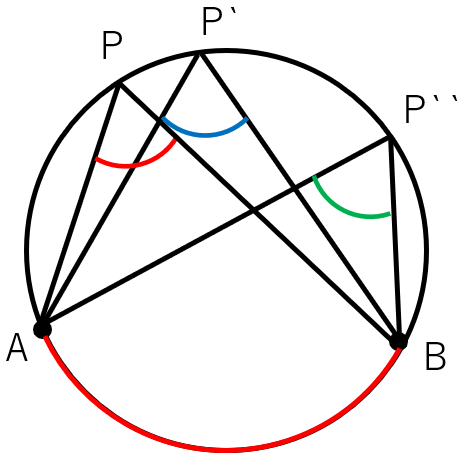
1つの弧に対する円周角の大きさは一定
∠APB=∠AP’B=∠AP‘‘B
円周角の性質にはもう一つ大事なものがあるから紹介するね。
円周角とその弧に対する中心角の関係
2つ目の円周角の性質は「円周角と中心角の関係」だよ。
結論は次の通り
円周角の定理②
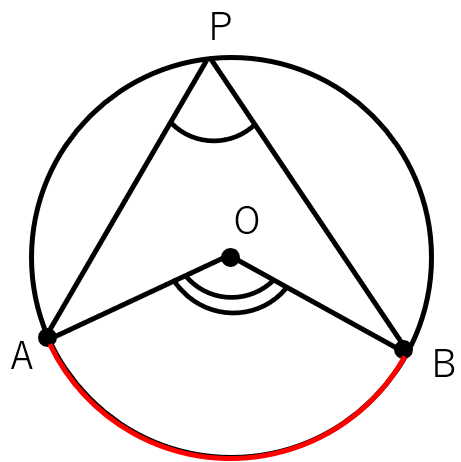
1つの弧に対する円周角の大きさは、その弧の中心角の大きさの半分
∠APB=\(\frac{1}{2}\)∠AOB
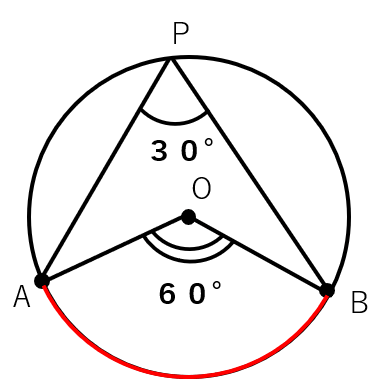
例えば、∠AOBが60°だったら∠APBは30°になるってことだよ。
なんで中心角の半分が円周角になるのかを考えていこう。
中心角の半分が円周角になる理由
POを結んで、「\(\overset{\frown}{AB}\) に対する円周角∠APB」を2つに分けよう。
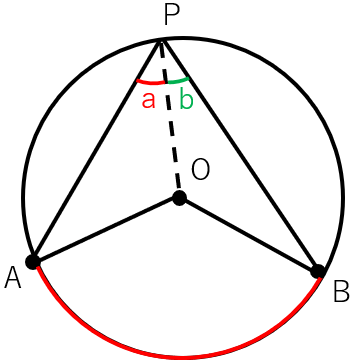
ここで次の長さは円の半径だから等しくなるよね。
OA=OB=OP
そうすると、色の付けた△OAPと△OBPは二等辺三角形ってことになるね。
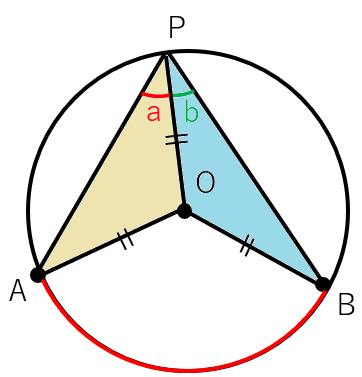
二等辺三角形の底角は等しくなるから、次のようになるよ。
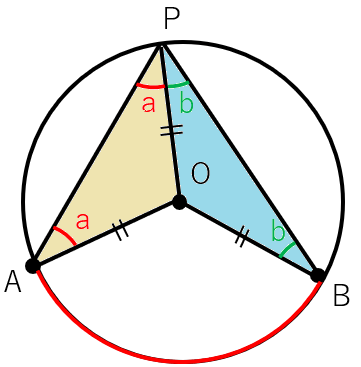
最後に三角形の外角の性質を使おう。
三角形の外角の性質
三角形の外角は、隣り合わない2つの内角をたしたものと等しい
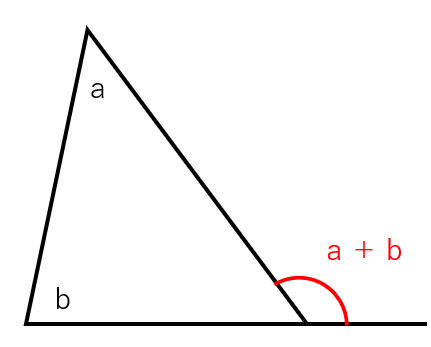
△AOPに注目しよう。
OPを延長して、三角形の外角の性質を使うと、
中心角の左側はa+a=2aになるよ。
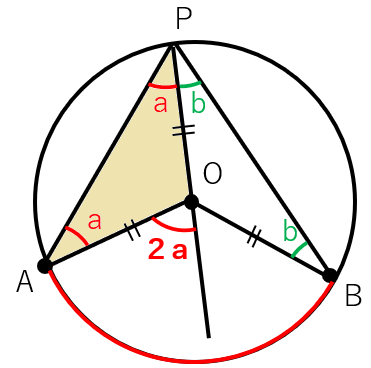
△BOPに注目しよう。
三角形の外角の性質を使うと、
中心角の左側はb+b=2bになるよ。
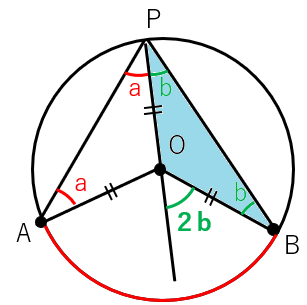
ということは、中心角∠AOBの大きさは2a+2bと表すことができるんだ。
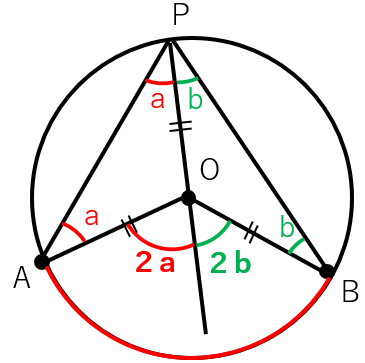
最後に\(\overset{\frown}{AB}\) に対する中心角と円周角の大きさを比べてみよう。
・中心角∠AOB=2a+2b
・円周角∠APB=a+b
→中心角の半分が円周角になることが説明できたね。
だから次の性質が成り立つってことだよ。
円周角の定理②
1つの弧に対する円周角の大きさは、その弧の中心角の大きさの半分
∠APB=\(\frac{1}{2}\)∠AOB

円周角の定理
円周角の定理は次の通りだよ。問題を解くときに必ず必要な知識だからしっかりマスターしよう。
円周角の定理
- 1つの弧に対する円周角の大きさは一定
∠APB=∠AP’B=∠AP‘‘B

- 1つの弧に対する円周角の大きさは、その弧の中心角の大きさの半分∠APB=\(\frac{1}{2}\)∠AOB

最初に紹介した「1つの弧に対する円周角の大きさは一定」という性質がなぜ成り立つかは説明していなかったけれど、
「1つの弧に対する円周角の大きさは、その弧の中心角の大きさの半分」の性質を使えば説明できちゃうよ。
1つの弧に対する円周角の大きさが一定になる理由
1つの弧に対する円周角の大きさは、その弧の中心角の大きさの半分だったから、
もし、\(\overset{\frown}{AB}\) に対する中心角が100°だったとしよう。
ことき、\(\overset{\frown}{AB}\) に対する円周角はすべて50°になるよね。
∠APB=∠AP’B=∠AP”B=50°
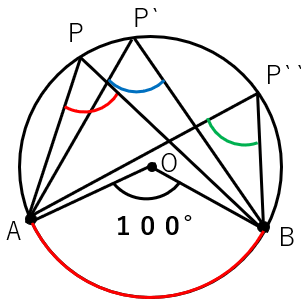
だから「1つの弧に対する円周角の大きさは一定」になるんだよ。
円周角の問題
円周角の定理を使って問題を解いていこう。
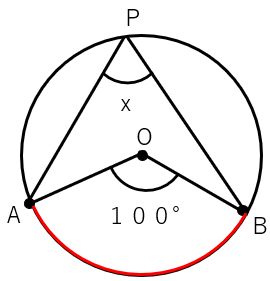
「1つの弧に対する円周角の大きさは、その弧の中心角の大きさの半分」だったよね。
この問題では中心角が100°だから、円周角xは100÷2=50°と求まるね。
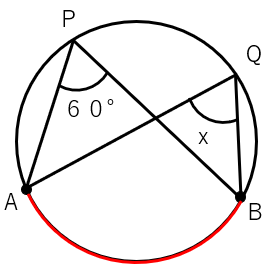
∠Pも∠Qも\(\overset{\frown}{AB}\) に対する円周角だから∠P=∠Qになるよね。
だから、x=60°と求められるよ。
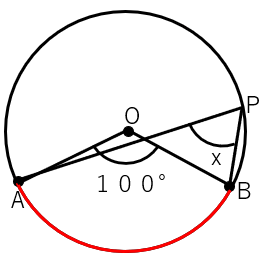
「初めて見る図形だな」と感じるかもしれないけど、
∠AOBは\(\overset{\frown}{AB}\) に対する中心角で、
求めたいxは\(\overset{\frown}{AB}\) に対する円周角
なのがわかるかな?
ということは、中心角100°の半分が円周角になるから、x=50°が答えだよ。
円周角の定理さえ知っていれば楽勝な問題だったね。ただ、次の問題は頭を使うと思うよ。
「中心を通らない」円周角の問題
「中心を通らない」場合の円周角の問題はどうやって解けばいいんだろう?と困ってしまうという意見が多かったので、ここで紹介するね。
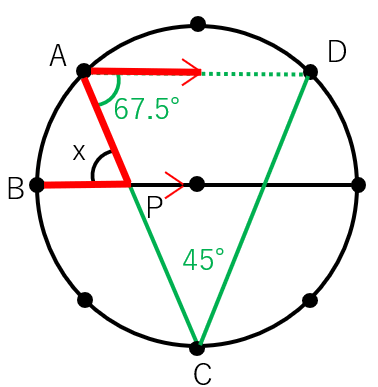
次の点は円周を8等分した点である。xの角度を求めなさい。
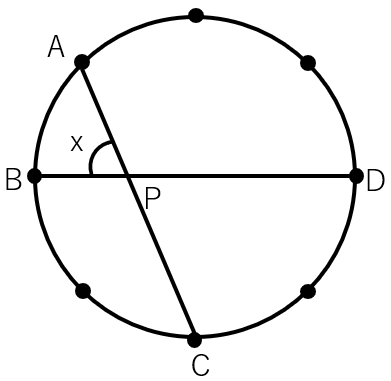
今までの問題と比べると中心も書いていないし、角度も書いていないから難しく感じるよね。
このまま眺めていても何も進まないから、中心Oをとって次のように赤線で結ぼう。
\(\overset{\frown}{AD}\)は点2つ分だから、中心角は90°になるよね。
なぜなら
8つ分で360°
1つ分は360°÷8=45°
2つ分だから45°×2=90°
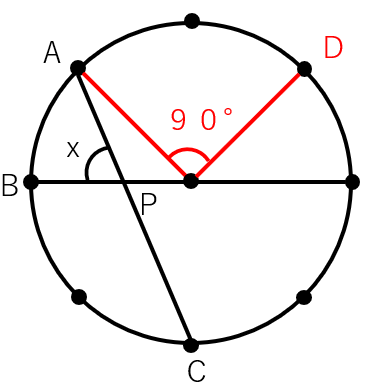
次にCとDを次のように緑線で結ぼう。
「1つの弧に対する円周角は中心角の半分」だったから、
∠C=90°÷2=45°と求まるね。
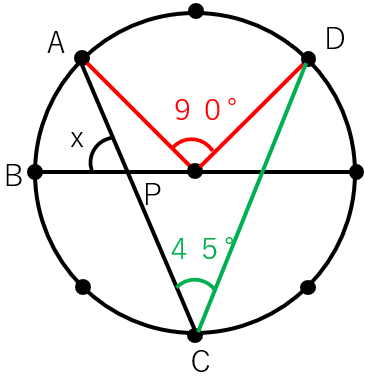
次にADを結ぶと、△ACDは二等辺三角形になっているよね。
二等辺三角形の底角は等しくなるから、
∠Aと∠Dの大きさは等しいよ。
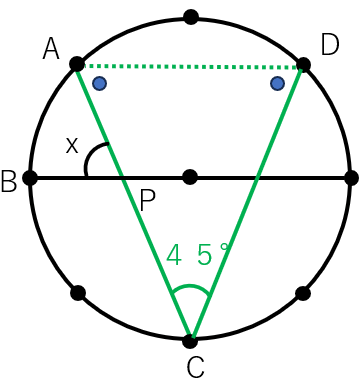
△ACDの内角の和は180°だから、∠Aの角度は
180°-45°=135°
135°÷2=67.5° ←底角は等しいから÷2をしているよ。
と求められるね。
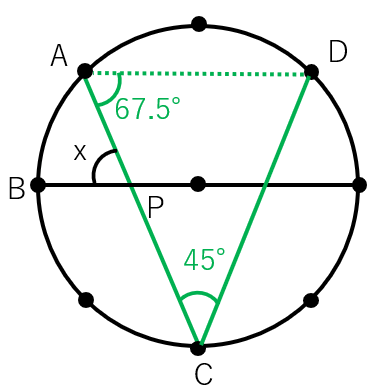
最後に平行線の錯角は等しいから、x=67.5°と求まったね。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。

-
設問のGの位置が違ってますよ
-
大変分かりやすく説明頂きましたすぐ忘れるとおもいますが納得です。ありがとうございました
。

すごく分かりやすかったです。
お陰様でテストは100点でした!