「乗法公式」とは?乗法公式一覧とやり方・覚え方をくわしく解説
中学3年生の数学で学習する「乗法公式」について、乗法公式を覚える理由や、どんな乗法公式があるのかの一覧、乗法公式を使った式の展開のやり方などをくわしく解説していくよ。
乗法公式の覚え方も紹介するよ。
乗法公式とは
多項式の乗法(展開)の学習では、(多項式)×(多項式)の計算のやり方を解説したね。
基本的には、
(a+b)(c+d)=ac+ad+bc+bd
というように、「順番にかけていく」計算方法だったね。
でも、ひとつひとつ順番にかけていくのって、少し大変だよね。
時間もかかってしまうし、うっかり順番を飛ばしてしまったりというミスも起きてしまうかもしれない。
それを解決してくれるのが、これから学習する「乗法公式」なんだよ。
「乗法公式」というのは、(多項式)×(多項式)の計算を速くするための方法なんだ。
大事だからもう一度言うよ。
「乗法公式は計算を速くするための方法!」だよ。
だから最悪、乗法公式を覚えていなくても、なんとかなるんだけど、ほとんどの受験生が覚えているし、中学3年生で学習する「因数分解」という単元で大活躍するよ。だから、今のうちに覚えておこう。
(x+a)(x+b)の形をした式の展開のしかた
「乗法公式」は、いわゆるショートカットの便利ワザなので、まずはそもそもの展開の基本をもとに説明するよ。
「基本」があってこその、「ショートカット」だからね。
まずは「(x+a)(x+b)」の形をした式の展開の基本を復習をしよう。
「式の展開の基本」は下のとおりだったね。
多項式×多項式の展開の基本
(a+b)(c+d)=ac+ad+bc+bd
基本となる展開のしかたでは「(a+b)(c+d)」だけれど、乗法公式はxを使っているので、xを使った形に変えて説明していくね。
「(x+a)(x+b)」の形をした式でも、登場している文字が違うだけだから、展開するときは基本と同じように順番にかけていったらいいから安心してね。
(x+a)(x+b)を順番にかけていくと次のようになるよ。
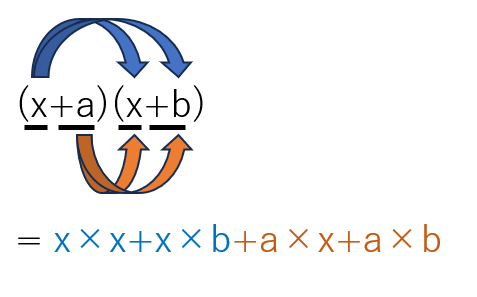
=x×x+x×b+a×x+a×b
=x2+bx+ax+ab ←bxとaxの順番を入れ替えるよ。
=x2+ax+bx+ab
ここまでは、展開の基本の通りだから何も問題ないよね。
さて、この「x2+ax+bx+ab」という式、もうすこし簡単にできることに気が付くかな?
「x2+ax+bx+ab」の「ax と bx」って、おなじxの項なので、計算できるよね。なので、計算してしまって、式を次のように形を変えてあげるよ。
=x2+(a+b)x+ab
この「x2+(a+b)x+ab」が、「(x+a)(x+b)」という式の形を展開したときの完成だね。
つまり、(x+a)(x+b)という形の場合、展開すると完成はかならず「x2+(a+b)x+ab」になるよ、ということだね。
さて、この「x2+(a+b)x+ab」。かならずこの形になることが分かっているんだったら、(x+a)(x+b)というはじめの式をみただけでも簡単に完成形を求めることができるよね。
だって、
・最初は「x2」がきて、
・次に「a」と「b」を足したものに「x」をかけてあげて、
・最後に「a」と「b」をかけたものがくる。
このテンプレートにあてはめるだけだからね。
例題で確かめてみよう。
たとえば、(x+2)(x+3)の式を展開するとするよ。
aにあてはまるのは「2」で、bにあてはまるのは「3」だね。
展開の基本の方法で計算しようとすると、
(x+2)(x+3)
=x×x+x×3+2×x+2×3
=x2+3x+2x+6
=x2+5x+6
というふうになるね。
これを、さっき形を変えて作った式「x2+(a+b)x+ab」を使って計算してみよう。
(x+2)(x+3)
=x2+(2+3)x+6
=x2+5x+6
どうかな?
すごくラクにできるよね。
つまり、「本当だったら、ひとつひとつ計算していた展開」を、「この式の形を展開した場合は、結局こういう形になるよね」ということが分かっているので、「だったら途中の細かい計算は省略して、出来上がりの形のテンプレートに、数字を当てはめるだけで計算できるようにしちゃおう!」ということ。
この、テンプレートが「乗法公式」ということだね。
(x+a)(x+b)の形をした式の展開
(x+a)(x+b)
=x2+(a+b)x+ab ←これが完成形!
なので、(x+a)(x+b)の形をした式には
「x2+(a+b)x+ab」という乗法公式が使える。
(x+a)2の形をした式の展開のしかた
(x+a)2の形をした式の展開には、どんな乗法公式がつかえるのだろう?
そのためには、(x+a)2を展開すると、どんな完成形になるかを復習しよう。
「(x+a)2」は、「(x+a)(x+a)」と表すこともできるよね。
この形にできちゃえば、あとは展開の基本を使えば、展開することができるよね。
(x+a)2
=(x+a)(x+a) これを順番にかけていくと次のようになるよ。
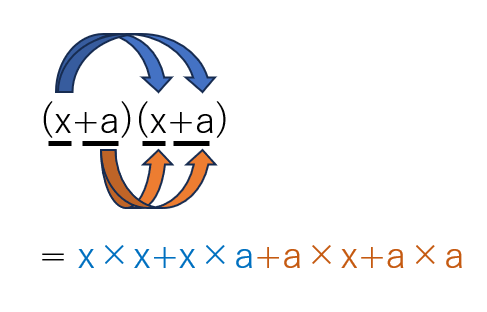
=x×x+x×a+a×x+a×a
=x2+ax+ax+a2 ←ax+ax=2axになる
=x2+2ax+a2
つまり、
・最初は「x2」がきて、
・次に「2」と「a」と「x」をかけたものがきて、
・最後に「aの二乗」がくる。
ということだね。
(x+a)2の形をした式の展開
(x+a)2
=x2+2ax+a2 ←これが完成形!
なので、(x+a)2の形をした式には
「x2+2ax+a2」という乗法公式が使える。
(x-a)2の形をした式の展開のしかた
(x-a)2の形をした式の展開では、どんな乗法公式が使えるのかな。
まずは展開の完成がどうなるかを考えてみよう。
(x-a)2=(x-a)(x-a)
さっきの「(x+a)2」と同じように、この形にできちゃえば、あとは展開の基本を使えば、展開することができるよね。
(x-a)2
=(x-a)(x-a) これを順番にかけていくと次のようになるよ。
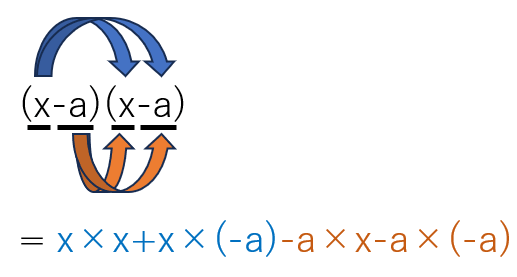
=x×x+x×(-a)-a×x-a×(-a)
=x2-ax-ax+a2 ←-ax-ax=-2axになるよ。
=x2-2ax+a2
つまり、
・最初は「x2」がきて、
・次に「-2」と「a」と「x」をかけたものがきて、
・最後に「aの二乗」がくる。
ということだね。
(x-a)2の形をした式の展開
(x-a)2
=x2-2ax+a2 ←これが完成形!
なので、(x-a)2の形をした式には
「x2-2ax+a2」という乗法公式が使える。
(x+a)(x-a)の形をした式の展開のしかた
最後に(x+a)(x-a)の形をした式の展開にはどんな乗法公式が使えるかを確認しよう。
今までと同じように、展開の基本を使うと次のようになるよ。
(x+a)(x-a)
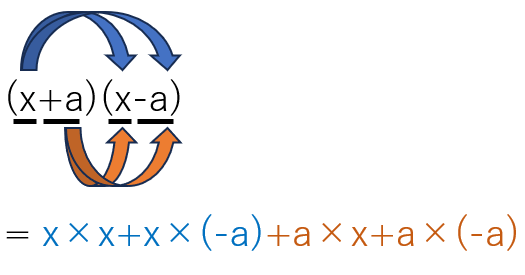
=x×x+x×(-a)+a×x+a×(-a)
=x2-ax+ax-a2 ←-ax+ax=0になるよね。
=x2-a2
つまり、
・最初は「x2」がきて、
・次にマイナスの「aの二乗」がくる。
ということだね。
(x+a)(x-a)の形をした式の展開
(x+a)(x-a)
=x2-a2 ←これが完成形!
なので、(x+a)(x-a)の形をした式には
「x2-a2」という乗法公式が使える。
乗法公式一覧と覚え方
今まで確認してきて、みつけた乗法公式は下の4つだよ。
乗法公式
1、(x+a)(x+b)=x2+(a+b)x+ab
2、(x+a)2=x2+2ax+a2
3、(x-a)2=x2-2ax+a2
4、(x+a)(x-a)=x2–a2
いきなりこの4つを覚えよう!と言われても、なかなか覚えられないよね。
だから、覚え方を紹介するね。
(x+a)(x+b)=x2+(a+b)x+abの覚え方
(x+a)(x+b)のような(x )(x )のような形の式を展開すると
x2+○x+△のようになるんだ。
あとは、○と△がわかればいいんだけど、○にはa+bの和が、△にはa×bの積が入るんだ。
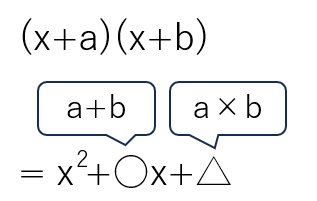
覚え方は「仲間わ、右の積」
x2+○x+△の
真ん中の○には「和(足し算)」
右の△には「積(かけ算)」
が入るってことだよ。
(x+a)2=x2+2ax+a2の覚え方
(x+a)2みたいな「(前+後)2」の形の式を展開すると、「x2+2ax+a2」になる。
つまり、「前の2乗+後ろの2乗+2倍の前後」になるんだよね。
前の2乗+後ろの2乗+2倍の前後と覚える
・前の2乗=x2
・後ろの2乗=a2
・2倍の前後=2×x×a=2ax
よくある間違い
(x+a)2=x2+a2
「2倍の前後」を忘れているね。
(x-a)2=x2-2ax+a2の覚え方
(x-a)2は、(x+a)2の乗法公式の「2ax」の前の符号が「-(マイナス)」になるだけだから、簡単に覚えられそうだね。
(x+a)(x-a)=x2–a2の覚え方
(x+a)(x-a)のような(前+後)(前-後)のような形の式を展開すると、「x2–a2」になるよね。
つまり、「前の2乗-後ろの2乗」になるんだ。
前の2乗-後ろの2乗と覚える
・前の2乗=x2
・後ろの2乗=a2
もう一度確認すると乗法公式は速く展開するために大切なんだけど、忘れてしまっても、次の式さえ覚えていれば大丈夫。
(a+b)(c+d)=ac+ad+bc+bd
この式がもとになって乗法公式ができているからね。
乗法公式が使えない式も、もちろんある
ちなみに、乗法公式が使える式は、今まで見てきた4つのパターンだけなので、それに当てはまらない場合は乗法公式が通用しないよ。
乗法公式が通用しない問題は、展開の基本の式を使って展開する必要があるよ。
乗法公式を使った展開の問題
乗法公式が分かったところで、実際に乗法公式を使った展開の問題に挑戦してみよう。
乗法公式
1、(x+a)(x+b)=x2+(a+b)x+ab
2、(x+a)2=x2+2ax+a2
3、(x-a)2=x2-2ax+a2
4、(x+a)(x-a)=x2–a2
(x+a)(x+b)=x2+(a+b)x+abの問題
(1) (x+2)(x+3)を展開しなさい。
まず、(x+2)(x+3)のかっこの先頭に同じ文字「x」があることを確認しよう。
確認が終わったら次の乗法公式を使って展開しよう。
(x+a)(x+b)=x2+(a+b)x+ab
今回の問題では、「a=2」「b=3」だから、
(x+2)(x+3)は次のように乗法公式に当てはめることができるよ。
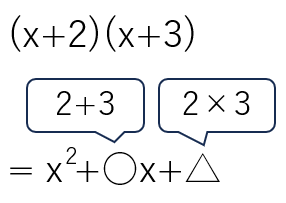
=x2+(2+3)x+2×3
=x2+5x+6
(2) (x-2)(x+3)を展開しなさい。
まず、(x-2)(x+3)のかっこの先頭に同じ文字「x」があることを確認しよう。
確認が終わったら次の乗法公式を使って展開しよう。
(x+a)(x+b)=x2+(a+b)x+ab
今回の問題では、「a=-2」「b=3」だから、
(x-2)(x+3)は次のように乗法公式に当てはめることができるよ。
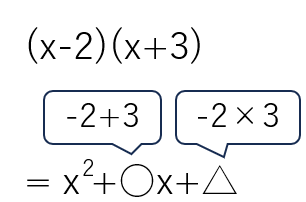
=x2+(-2+3)x+(-2)×3
=x2+x-6
(3) (x-2)(x-3)を展開しなさい。
まず、(x-2)(x-3)のかっこの先頭に同じ文字「x」があることを確認しよう。
確認が終わったら次の乗法公式を使って展開しよう。
(x+a)(x+b)=x2+(a+b)x+ab
今回の問題では、「a=-2」「b=-3」だから、
(x-2)(x-3)は次のように乗法公式に当てはめることができるよ。
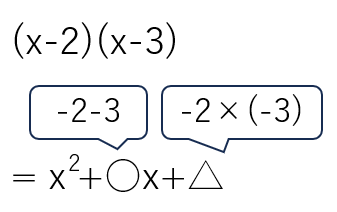
=x2+(-2-3)x+(-2)×(-3)
=x2-5x+6
(x+a)2=x2+2ax+a2の問題
(x+3)2を展開しなさい。
「(前+後)2」の形になっているから、「前の2乗+後ろの2乗+2倍の前後」が使えるよ。
・「前の2乗」=x2
・「後ろの2乗」=32=9
・「2倍の前後」=2×x×3=6x
だから
(x+3)2
=x2+9+6x
=x2+6x+9
最後は次数が大きい順に並び変えたよ。(x2→x)
(x-a)2=x2-2ax+a2の問題
(x-3)2を展開しなさい。
「(前-後)2」の形になっているから、「前の2乗+後ろの2乗-2倍の前後」が使えるよ。
・「前の2乗」=x2
・「後ろの2乗」=32=9
・「2倍の前後」=2×x×3=6x
だから
(x-3)2
=x2+9-6x ←「2倍の前後」の前が「-(マイナス)」になることに気をつけよう。
=x2-6x+9
(x+a)(x-a)=x2–a2の問題
(1) (x+3)(x-3)を展開しなさい。
「(前+後)(前-後)」のような形になっているから、展開すると「前の2乗-後ろの2乗」になるよ。
・「前の2乗」=x2
・「後ろの2乗」=32=9
だから
(x+3)(x-3)
=x2-9
(2) (4+x)(4-x)を展開しなさい。
「(前+後)(前-後)」のような形になっているから、展開すると「前の2乗-後ろの2乗」になるよ。
・「前の2乗」=42=16
・「後ろの2乗」=x2
だから
(4+x)(4-x)
=16-x2
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。


