「二次方程式の利用」色々な問題の解き方「図形・動点・容積など」
中学校3年生の数学で学習する「二次方程式の利用」について、二次方程式を使って、色々なパターンの問題を解く方法をわかりやすく解説するよ。
定期テストや入試でよく出る「整数の問題」「速さ・割合の問題」「図形の問題」「容積の問題」「動く点の問題」など、ひとつずつ確認しよう!
「二次方程式の利用」とは、つまり色々な数学の問題を、二次方程式で表すことで、効率的に解こうということ。「二次方程式」を問題を解くために「利用」するんだね。
ただ、その利用の方法が、問題のパターンごとに変わってくるので、それぞれのパターンごとに、どうやって二次方程式を使ったら良いのかを解説していくよ。
二次方程式の利用「整数の問題」
「ある整数」について、その整数がどんな数かヒントが書いてあって、そのヒントをもとに二次方程式に当てはめて、その整数がいくつかを考えるタイプの問題だよ。
それでは早速やってみよう。
問題
差が3の大小2つの整数があります。それぞれの整数を2乗した和が65になりました。2つの整数を求めなさい。
この問題の「ある整数」を求めるためのヒントは、
「差が3」
ということと、
「それぞれの整数を2乗した和が65になる」
ということだね。
イメージはこんな感じになるよ。
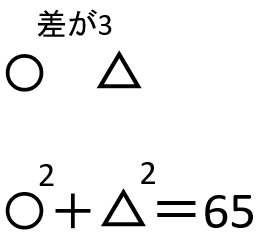
ただ、〇と△では2次方程式の計算が面倒になるので、文字を使って考えよう。
2つの整数のうち、小さい方を「x」とすると、差が3だから大きい方は「x+3」と表せるよね。
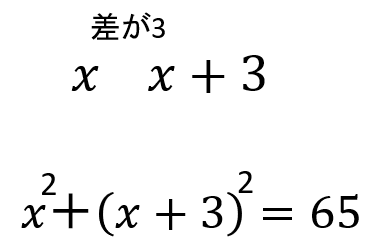
それぞれの整数を2乗した和が65になるから
x2+(x+3)2=65
という二次方程式をたてることができるよ。
二次方程式をたてることができたら、あとはそれを実際に解いて、xを求めればいいんだ。
そうすれば、「ある整数」が求まるよね。
x2+(x+3)2=65 ←(x+3)2を展開しよう
x2+x2+6x+9=65
2x2+6x+9-65=0
2x2+6x-56=0 ←両辺を「2」で割ろう
x2+3x-28=0 ←左辺を因数分解しよう
(x+7)(x-4)=0
x=-7,4
「x」は「-7」または「4」ということがわかったね。
「x」って、2つの整数のうち「小さい方」だったよね。
大きい方は「x+3」と表せるから、
x=-7のとき、大きい方は-7+3=-4
x=4のとき、大きい方は4+3=7
になるよ。
だから、差が3で、それぞれの整数の2乗の和が65に2つの整数は
-7と-4
または
4と7
になるよ。
もう1パターンやってみよう。
問題
連続する3つの整数をそれぞれ2乗した和が149になった。3つの整数のうち真ん中の整数を求めなさい。
この問題のイメージはこんな感じになるよ。
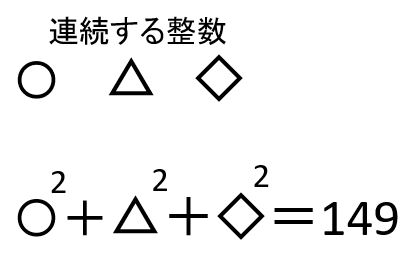
ただ、〇と△と◇では2次方程式の計算が面倒になるので、文字を使って考えよう。
3つの連続する整数のうち、真ん中の整数を「x」とすると、
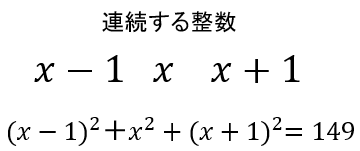
それぞれの整数を2乗した和が149なるから
(x-1)2+x2+(x+1)2=149
という二次方程式をたてることができるよ。
(x-1)2+x2+(x+1)2=149 ←左辺を展開しよう
x2-2x+1+x2+x2+2x+1=149 ←左辺を整理しよう
3x2+2=149
3x2+2-149=0
3x2-147=0 ←両辺を「3」で割ろう
x2-49=0
x2=49
x=±7
「x」は整数だから、x=-7もx=7もこの問題の答えに適しているね。
x=-7のとき、3つの整数は-8,-7,-6
x=7のとき、3つの整数は6,7,8
になるよ。
二次方程式の利用「公式を使う問題」
このパターンの問題では、ある数学の公式が提示されるので、その公式を使って、問題で指示されたことについて解けばいいだけだよ。
問題
n角形の対角線の本数は次のような式で表せます。
\(\frac{n(n-3)}{2}\) (本)
対角線の本数が152本になる多角形は何角形か。
n角形の対角線の本数は\(\frac{n(n-3)}{2}\) (本)と表せて、これが152本になるときだから、次のような方程式がたてられるよ。
\(\frac{n(n-3)}{2}\)=152
方程式を満たすnを求めたらOKってことだね。
\(\frac{n(n-3)}{2}\)=152
\(\frac{n(n-3)}{2}\)×2=152×2 ←分母の「2」を消すために両辺に「2」をかけるよ
n(n-3)=304 ←展開をしよう
n2-3n=304
n2-3n-304=0 ←因数分解をしよう
(n+16)(n-19)=0
n=-16,19
「n」ってn角形のnだったよね。
19角形はあっても-16角形なんて存在しないから、この問題ではn=-16は適していないよ。
だから、対角線が304本になるのは19角形とわかるね。
この問題のパターンのように、答えが「負の数ではありえない」など、2次方程式を解いて求めた答えがすべて適しているとは限らないときがあるんだ
求めた答えが、その問題の答えとして適しているかどうか?を毎回考える必要があるので注意しよう。
二次方程式の利用「速さ・割合の問題」
速さの問題
問題
ボールを秒速20mの速さで真上に投げるとき、
投げてからx秒後のボールの高さは(20x-5x2)mと表すことができる。
(1)ボールの高さがはじめて5mになるのは何秒後か。
(2)ボールが落ちてくるのは何秒後か。
(1)
ボールの高さがはじめて5mになる時間を求めよう。
ボールの高さは(20x-5x2)mと表せて、これが5mになるときだから次のような2次方程式になるよ。
20x-5x2=5 ←右辺の5を移項しよう
-5x2+20x-5=0 ←両辺を5で割ろう
-x2+4x-1=0 ←両辺に(-1)をかけて、「x2」の前の符号を「+」に
x2-4x+1=0
左辺は因数分解できないから解の公式を使って解を求めよう。
ax2+bx+c=0とx2-4x+1=0を比べると
a=1、b=-4、c=1とわかるね。
解の公式を使おう。
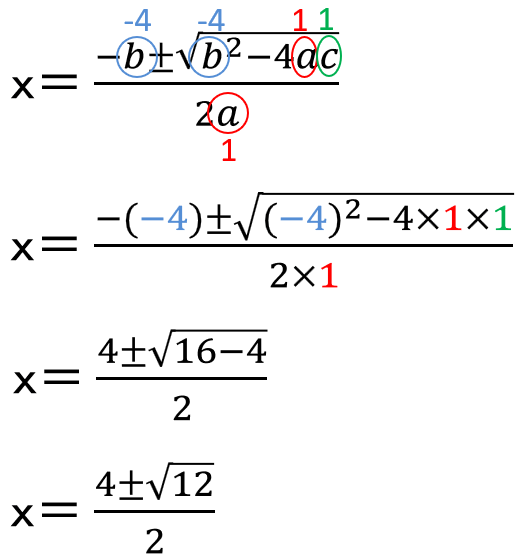
\(\sqrt{12}\)ってa\(\sqrt{b}\)の形にしたら2\(\sqrt{3}\)になって、約分もできるから
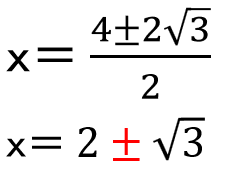
ボールが5mの高さになるのは、2-\(\sqrt{3}\)秒後と2+\(\sqrt{3}\)秒後と求まるよ。
なぜ2回あるかっていうと
ボールが上がっていくときと落ちていくときで2回5mになるタイミングがあるよね。
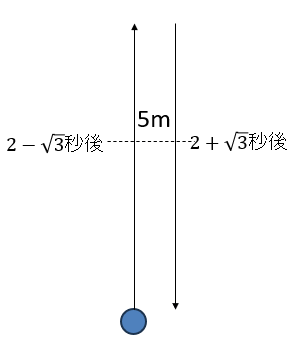
今回の問題では、はじめて5mになるのは何秒後かを求めるのだから、
答えは2-\(\sqrt{3}\)秒後だよ。
(2)
ボールが落ちてくるってことは、高さが0mになるってことだよね。
ボールの高さは(20x-5x2)mと表せて、これが0になるときだから次のような2次方程式になるよ。
20x-5x2=0
-5x2+20x=0 ←両辺を(-5)で割ろう
x2-4x=0 ←共通因数「x」でくくろう
x(x-4)=0
x=0,4
高さが0mになるのは、0秒後と4秒後だとわかるね。ただ、0秒後っていうのは投げる時だから、答えは4秒後ってことだね。
気を付けること
x2-4x=0
を見て「x」で割ったりしないようにしよう。文字が0になる可能性もあるからね。
方程式を解くときは、0で割ってはいけないという決まりがあったよね。
割合の問題
問題
原価500円の商品にx割の利益を見込んで定価をつけた。ただ、売れなかったためx割引きで売ったので、最終的な金額は480円で販売した。
xの値を求めよ。
割合ってただでさえイメージがしにくいのに、文字も出てくるから難しく感じると思うよ。
だからまずは数字で考えよう。
x=3としてみよう。
①原価500円の商品に3割の利益を見込んで定価をつけた。
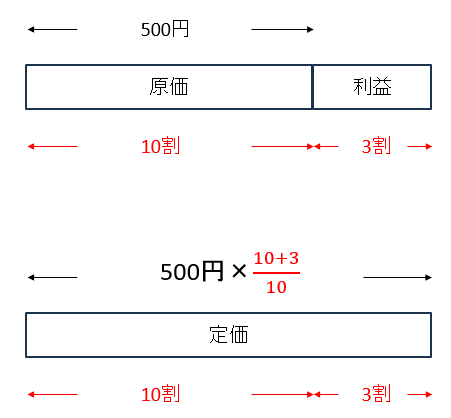
定価は500×\(\frac{10+3}{10}\)円と求まるよ。
②3割引きで売った
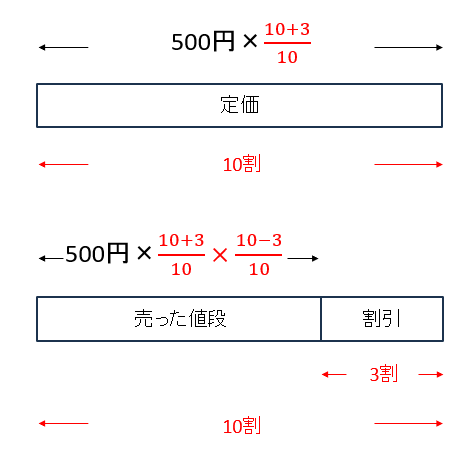
定価500×\(\frac{10+3}{10}\)円の商品を3割引きで売ったから、
売った値段は500×\(\frac{10+3}{10}\)×\(\frac{10-3}{10}\)円と求められるよ。
次に実際にxを使って考えていこう。「3」で計算していたところを「x」に変えればOK。
①原価500円の商品にx割の利益を見込んで定価をつけた。
定価は500×\(\frac{10+x}{10}\)円と求まるよ。
②x割引きで売った
売った値段は500×\(\frac{10+x}{10}\)×\(\frac{10-x}{10}\)円と求められるよ。
③最終的に売った値段は480円になることから方程式をたてる
500×\(\frac{10+x}{10}\)×\(\frac{10-x}{10}\)=480
④方程式を解いて、xの値を求める
500×\(\frac{10+x}{10}\)×\(\frac{10-x}{10}\)=480
5×(10+x)(10-x)=480 ←両辺を「5」で割ろう
5で割ると左辺が5÷5=1になって式が簡単になるよ。
5×(10+x)(10-x)÷5=480÷5
(10+x)(10-x)=96 ←左辺を展開しよう
100-x2=96 ←式を整理しよう。
100-x2-96=0
4-x2=0
x2=4
x=±2
「x」って割合だよね。
x=-2っていうことは「-2割」になるね。
「-2割」という表し方は正しくないから、答えは2割だよ。
二次方程式の利用「図形の問題」
問題
下の図のような正方形の畑に幅2mの道を作ると、残りの畑の面積は48m2になった。畑の1辺の長さを求めなさい。
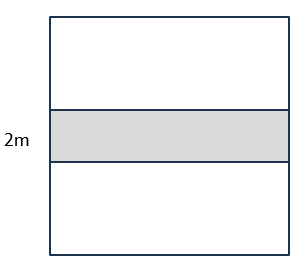
このような問題を解くコツは、図形を解きやすいように形を変えたりできないか考えること。
たとえばこの問題の場合、真ん中にある「幅2mの道」を下に移動しても、求めるべき「残った畑の面積」は変わらないよね。
このほうが、断然計算しやすくなるね。
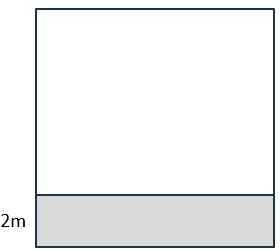
正方形の1辺の長さをxmとすると、残った畑の縦と横の長さは次のようになるよ。
横の長さはxm、縦の長さはxmから道幅2mを引いた長さだから(x-2)m。
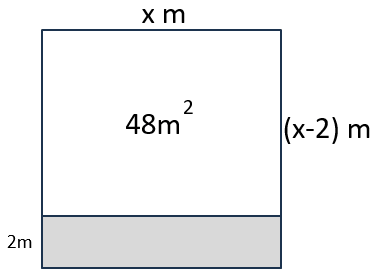
残った畑の面積は縦×横で求めることができて、これが48m2になるから
(x-2)×x=48
という方程式がたてられるね。
(x-2)×x=48 ←展開しよう
x2-2x=48
x2-2x-48=0 ←因数分解しよう
(x-8)(x+6)=0
x=8,-6
xは正方形の1辺の長さなので、「-(マイナス)」はありえないよね。だから答えは8mになるよ。
二次方程式の利用「容積の問題」
問題
横の長さが縦の長さより5cm長い長方形の紙がある。この紙の4つの角から1辺2㎝の正方形を切り取り、直方体の容器をつくると、容積は132cm3になった。
はじめの紙の縦を求めなさい。
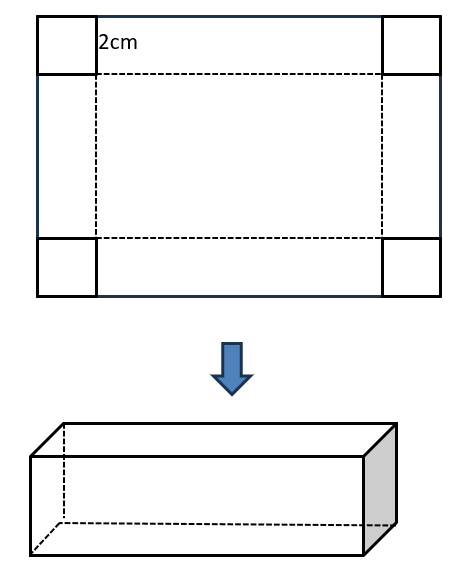
まず、求めたい長方形の紙の縦の長さをxcmとしよう。
横の長さは縦よりも5cm長いから、(x+5)cmと表せるよね。
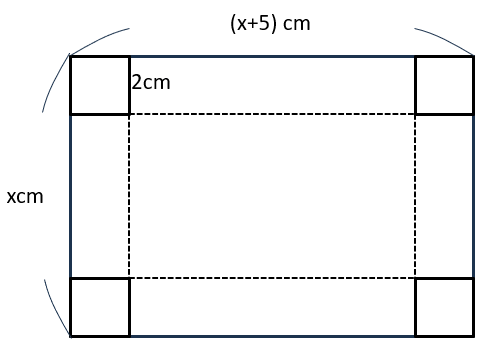
今回の問題では、長方形の紙を組み立てて直方体を作るんだけど、
イメージできているかな?
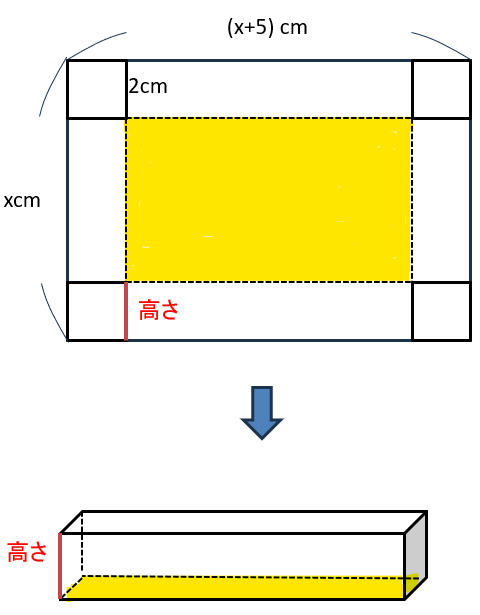
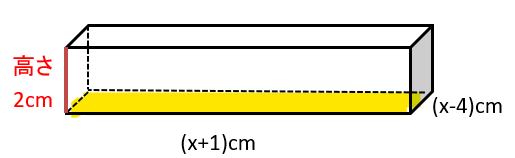
・黄色で塗ったところが直方体の底面積
・直方体の高さは赤で表した長さ
黄色で塗った底面の縦と横の長さを求めてみよう。
縦の長さは
xcmから四隅の2㎝を2つ分引いて
x−2−2=(x−4)cm
横の長さは
(x+5)cmから四隅の2㎝を2つ分引いて
(x+5)−2−2=(x+1)cm
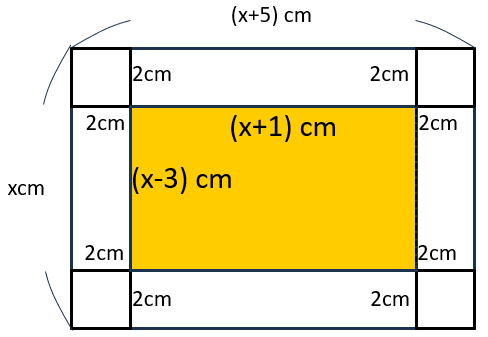
直方体の容積は
縦×横×高さで求めることができるね。
容積は132cm2になるから、次のような方程式がたてられるよ。
(x-4)×(x+1)×2=132
(x-4)(x+1)×2÷2=132÷2 ←両辺を「2」で割ろう
(x-4)(x+1)=66 ←左辺を展開しよう
x2-3x-4=66
x2-3x-4-66=0
x2-3x-70=0 ←因数分解しよう
(x-10)(x+7)=0
x=10,-7
「x」は長方形の縦の長さだったから「-(マイナス)」はありえないよ。だから答えは10cmと求まるね。
二次方程式の利用「動点の問題」
動点の問題とは、図形上にある「点P」などが、図形の辺などの上を移動するパターンの問題だよ。
問題
1辺が15cmの正方形ABCDがあります。点Pは、秒速1cmで点Aから点Bまで動きます。点Qは、秒速1cmで点Bから点Cまで動きます。
P、Qが同時に出発するとき、△PBQの面積が25cm2になるのは何秒後か。
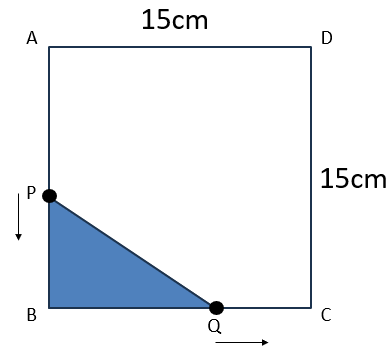
x秒後に△PBQの面積が25cm2になったとしよう。
点Pも点Qも1秒で1cm動くから、x秒だとxcm動くよね。
x秒後の△PBQは下の図のようになっているよ。
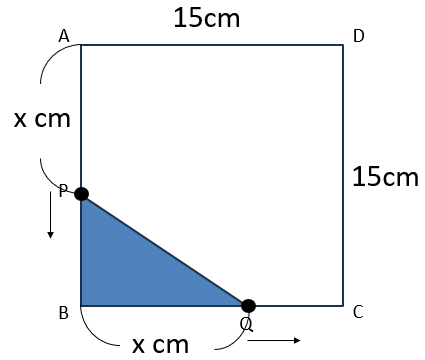
△PBQの面積はPB×BQ÷2で求まるから
PBの長さを求めよう。
PBの長さは正方形の1辺の長さ15cmからAPの長さxcmを引けばいいから
PB=(15-x)cm
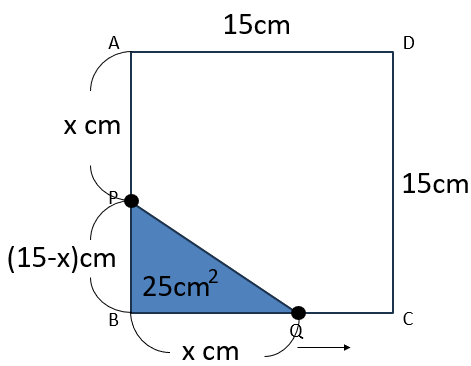
x秒後に△PBQの面積が25cm2だとすると、次の方程式がたてられるよ。
△PBQの面積=PB×BQ÷2=25
x×(15-x)÷2=25
x(15-x)÷2×2=25×2 ←両辺に「2」をかけよう
x(15-x)=50 ←展開しよう
15x-x2=50
15x-x2-50=0
-x2+15x-50=0 ←両辺に「-1」をかけよう
x2-15x+50=0 ←因数分解しよう
(x-5)(x-10)=0
x=5,10
解は2つあるけど、どちらとも答えにしてもいいのかを考えよう。
正方形の1辺の長さは15cmで、点P、点Qは15秒でゴールするよね。
ということは、5秒後、10秒後は条件を満たしているから、両方とも答えにしていいってことになるね。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。



