円周角の定理を使った相似の証明(円と交わる直線でできる図形)
中学3年生の数学で学習する「円周角の定理の利用」について、円と交わる直線でできる図形が、相似であることを円周角の定理を使って証明する方法をわかりやすく解説するよ。
円の内部に点Pを取った場合と、円の外部に点Pを取った場合、それぞれの場合の円と交わる直線でできる図形が相似になることを確かめよう。
高校で学習する「方べきの定理」についても触れるよ。
円周角の定理は、どんなことに利用できるだろう?
ここでは、円と交わる直線でできる図形が相似であることを、円周角の定理を使って証明するよ。
また、相似であることを利用して、図形の辺の長さを答える問題の解き方も紹介するよ。
円の内部に点Pを取った場合
円の内部に、点Pを取って、Pを通る2つの直線を引いたとするよ。
そして、その直線と円の交点どうしを結んでみるよ。
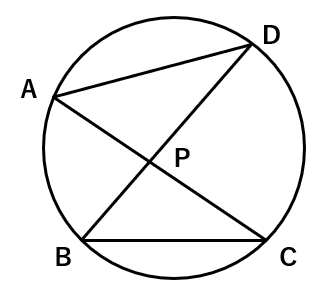
すると、このような2つの三角形が円の中にできるんだ。
実はこの2つの三角形は相似になるんだよ。
では、円周角の定理を使ってこの2つの三角形が相似であることを証明していくよ。
下の図で△APD∽△BPCになることを証明しなさい。

結論から先に言うと、相似条件は
2組の角がそれぞれ等しいになるよ。
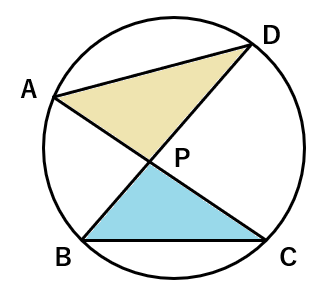
では、「2組の角」とはどこなのかを考えよう。
円周角の定理
「1つの弧に対する円周角の大きさは一定」という性質を使うと
\(\overset{\frown}{AB}\)に対する円周角は等しいから
∠ADP=∠BCP ・・・①
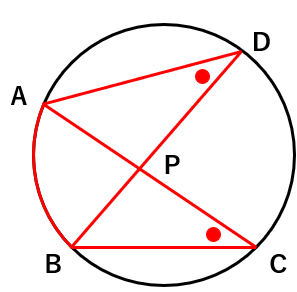
\(\overset{\frown}{CD}\)に対する円周角は等しいから
∠DAP=∠CBP ・・・②
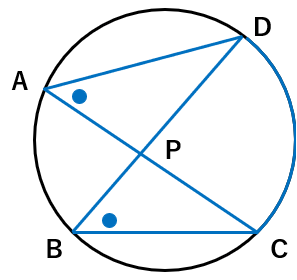
①②より、2組の角がそれぞれ等しいので
△ABP∽△BCP
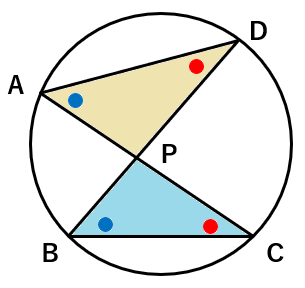
ここでは円周角の定理を2回使ったけれど、1回にすることもできるんだ。
なぜかというと、対頂角が等しいから、∠APD=∠BPCになるからね。
次の図のような「2組の角」とすることもできるよ。
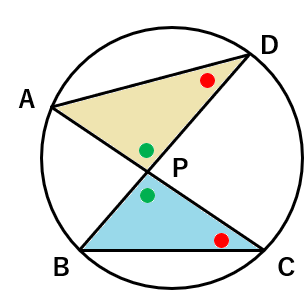
相似の証明はこれで終わりなんだけど、相似であることからわかることは何か考えてみよう。
相似からわかること
2つの図形が相似であることからわかることは何だろう?
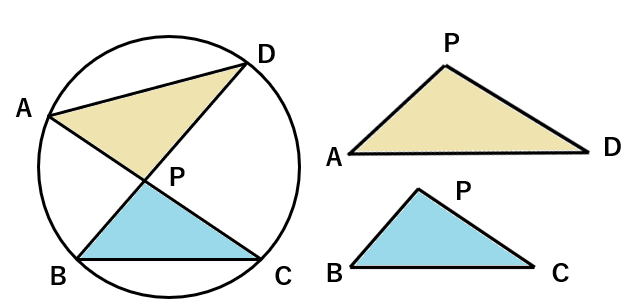
相似な図形の性質を思い出してみよう。
相似な図形の性質
相似な図形の対応する辺の長さの比はすべて等しい。
相似な図形の対応する角の大きさはそれぞれ等しい。
この性質を使うと次の2つのことがわかるよ。
相似な図形の対応する辺の長さの比はすべて等しい。
→AP:BP=AD:BC=DP:CP
相似な図形の対応する角の大きさはそれぞれ等しい。
→∠APD=∠BPC、∠A=∠B、∠D=∠C

相似であることから長さを求める問題
円と交わる直線でできる図形(今回は三角形)が相似であるということは、次のように図形の1辺の長さがわからない場合でも、相似な図形の性質を使って求めることができるね。
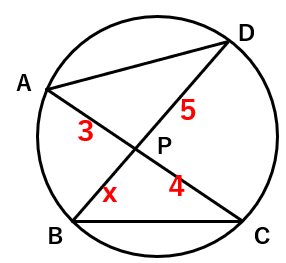
△ADP∽△BCPで、対応する辺の比は等しいから、
AP:BP=DP:CP
数字を代入して
3:x=5:4
比例式を解いてxを求めよう。
3:x=5:4
x×5=3×4
5x=12
x=\(\frac{12}{5}\)
円の外部に点Pを取った場合
おなじく点Pを取って、Pを通る2つの直線を引くんだけれど、今度は点Pが円の外部にある場合について考えていこう。
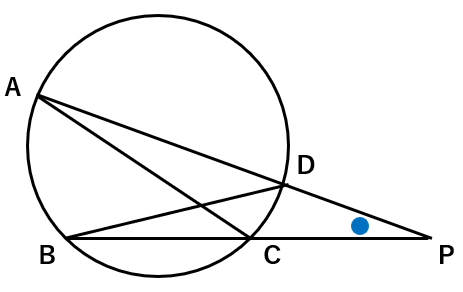
円の外部に点Pを取って、Pを通る2つの直線を引いたとするよ。
そして、その直線と円の交点どうしを結んでみるよ。
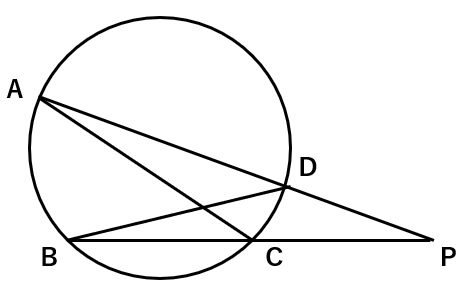
すると、このような2つの三角形が円の中にできるんだ。
この2つの三角形も相似になるんだよ。
では、円周角の定理を使ってこの2つの三角形が相似であることを証明していくよ。
下の図で△ACP∽△BDPを証明しなさい。

結論から先に言うと、相似条件は
2組の角がそれぞれ等しいになるよ。
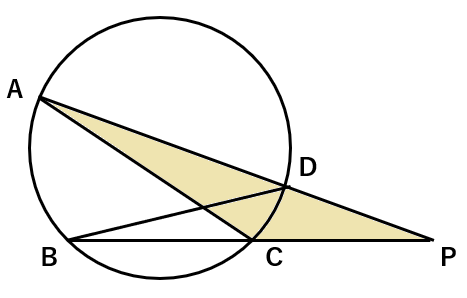
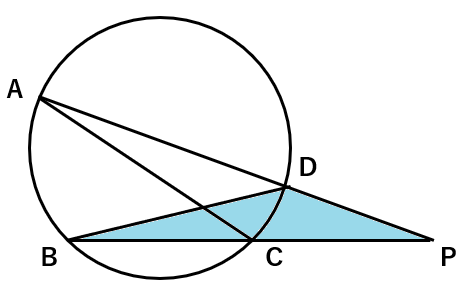
では、2組の角ってどこなのかを考えよう。
円周角の定理
「1つの弧に対する円周角の大きさは一定」という性質を使うと
\(\overset{\frown}{CD}\)に対する円周角は等しいから
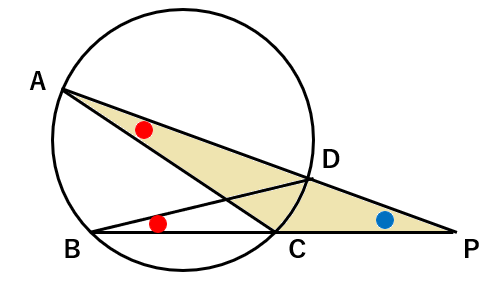
∠PAC=∠PBD ・・・①
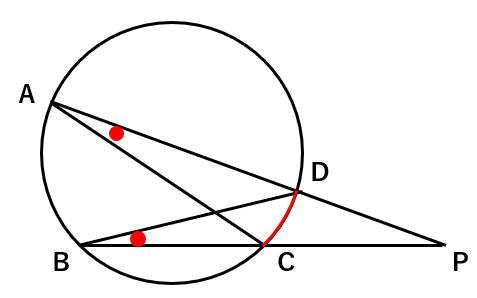
あと、∠Pはどちらの三角形にもあるから、
∠Pは共通 ・・・②
①②より、2組の角がそれぞれ等しいので
△ACP∽△BDP
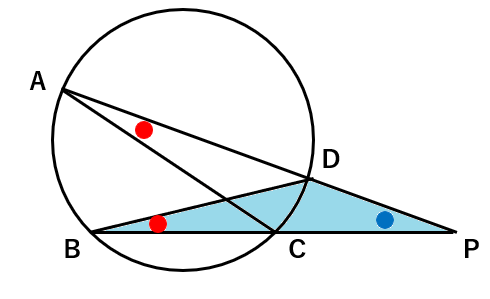
相似の証明はこれで終わりなんだけれど、相似であることからわかることは何か考えてみよう。
相似からわかること
2つの図形が相似であることからわかることは何だろう?
相似な図形の性質を思い出してみよう。
相似な図形の性質
相似な図形の対応する辺の長さの比はすべて等しい。
相似な図形の対応する角の大きさはそれぞれ等しい。
この性質を使うと次の2つのことがわかるよ。
相似な図形の対応する辺の長さの比はすべて等しい。
→AC:BD=CP:DP=PA:PB
相似な図形の対応する角の大きさはそれぞれ等しい。
→∠A=∠B、∠ACP=∠BDP、∠APC=∠BPD

相似であることから長さを求める問題
円と交わる直線でできる図形(今回は三角形)が相似であるということは、今回も図形の1辺の長さがわからない場合に、相似な図形の性質を使って求めることができるね。
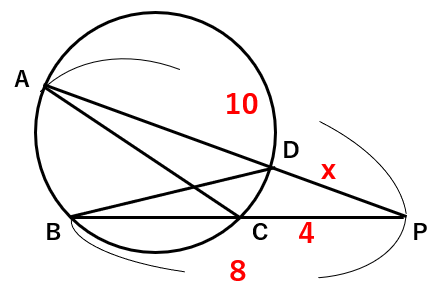
△ACP∽△BDPで、対応する辺の比は等しいから、
→CP:DP=PA:PB
数字を代入して
4:x=10:8
比例式を解いてxを求めよう。
4:x=10:8
x×10=4×8
10x=32
x=\(\frac{16}{5}\)
方べきの定理
今回学習した内容は、高校生になって「方べきの定理」という名前で再登場するんだよ。
方べきの定理は少し前まで中学3年生で習う内容だったんだけど、今は高校1年生の内容になっているよ。
方べきの定理とは次の通り。
方べきの定理
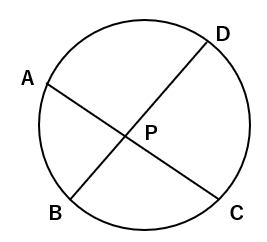
①PA:PC=PD:PB
②PA:PD=PB:PC
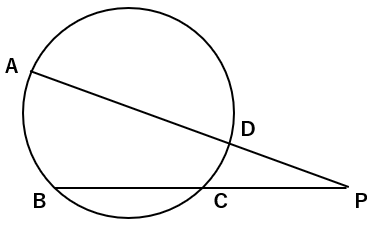
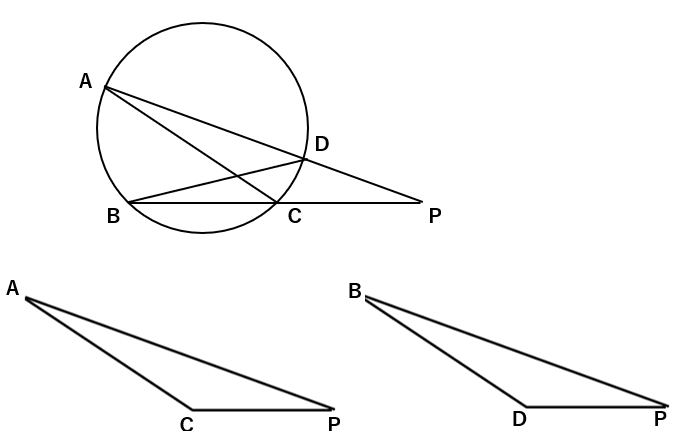
方べきの定理が成り立つことの証明だけれど、今回学習した「円と交わる直線でできる図形」が相似になることで説明できるよね。
例えば、①なら、ADとBCを結ぶと、△ADP∽△BCPになることがさっき分かったよね。

②なら、ACとBDを結ぶと、△ACP∽△BDPになるんだったよね。


高校生で習う「方べきの定理」はなんとなく知っておくと便利かもしれないよ。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。


