多項式の乗法「展開する」とは？多項式と多項式の乗法を解説

中学３年生の数学で学習する「多項式と多項式の乗法」について、(a+b)(c+d)の計算のやり方をわかりやすく解説するよ。

(a+b)(c+d)のように、多項式と多項式の乗法でおこなう「展開」とはどういうものかを紹介するよ。

多項式の乗法「展開する」とは？ 多項式と多項式の乗法を解説のPDF（8枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• (a+b)(c+d)を計算してみよう
• 「展開する」とは

(a+b)(c+d)を計算してみよう

今までの学習で、多項式と単項式の乗法（かけ算）はやってきたよね。
では、多項式と多項式の乗法はどうだろう。

たとえば、「(a+b)(c+d)」の計算がどうなるかを考えてみるよ。

(a+b)(c+d)という式では、（　）と（　）の間に「×（かける）」が省略されているよね。なので「 (a+b)×(c+d) 」というように「かけ算」をするんだよね。

今から、「多項式と多項式のかけ算」の計算をするための考え方を２つ紹介するね。

(a+b)(c+d)の計算するための考え方①

(a+b)(c+d)の計算を図で考えてみよう。

(a+b)×(c+d)っていうのは、たとえば縦が(a+b)、横が(c+d)の面積を求める計算として考えることができるよね。
なぜなら「長方形の面積」は、縦×横で求まるからね。

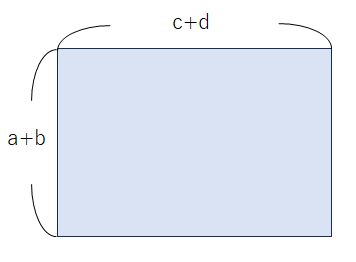
上の長方形の縦は(a+b)、横が(c+d)なので、縦を「a」と「b」に分けて、横も「c」と「d」に分ければ、下のように「４つの長方形」に分けることができるね。

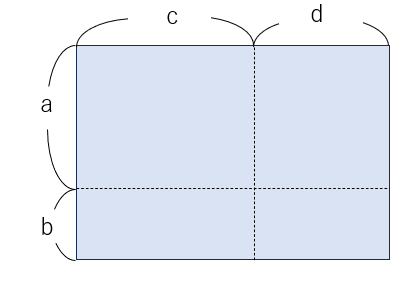
それでは、４つそれぞれの長方形の面積を順番に求めてみよう。

４つの長方形の面積を図に書くと次のようになるよ。

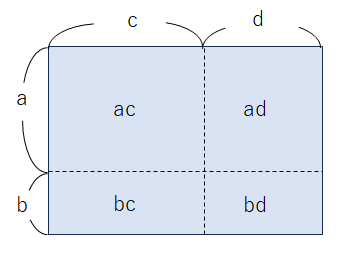
ということは、４つの長方形の面積の合計は「ac+ad+bc+bd」になるよね。

ここまでをまとめると次のようになるよ。

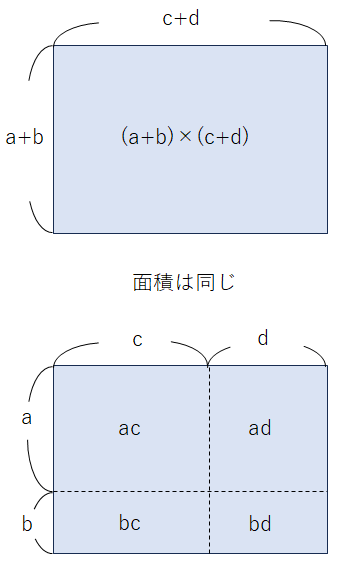
(a+b)×(c+d)とac+ad+bc+bdは同じ１つの長方形の面積を表しているから、

(a+b)(c+d)=ac+ad+bc+bd

と計算することができるよ。

この式はすごく大切な式だから覚えておこう。１年生でやった分配法則と同じように、次のように覚えるといいと思うよ。

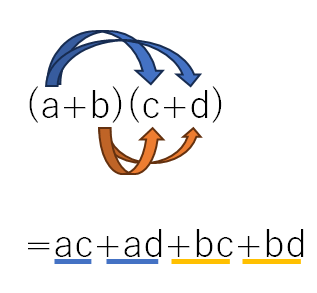
順番にかけていくようなイメージだね。

(a+b)(c+d)の計算をするための考え方②

さっきは長方形の図で説明したけれど、「式で説明する」こともできるよ。

たとえば、(a+b)=Mと置いてみよう。
そうすると、

(a+b)(c+d)
=M(c+d)

Mと(c+d)の間には「×（かける）」が省略されているから、

M(c+d)
=M×(c+d)
となるよね。　

M×(c+d)は、１年生でやった分配法則を使うと次のようになるよ。

M×(c+d)
=Mc+Md

ここで、Mを元に戻そう。←Mを(a+b)にかえる

Mc+Md
=(a+b)c+(a+b)d ←分配法則でかっこをはずす。

=ac+bc+ad+bd

(a+b)(c+d)を計算すると、ac+bc+ad+bdになることが式を使って説明できたね。

多項式×多項式「(a+b)(c+d)」の練習問題

(a+b)(c+d)=ac+ad+bc+bdになることをふまえて、練習問題に挑戦してみよう。それぞれでよくある間違いも紹介するよ。

(1)

(a+3)(b+2)

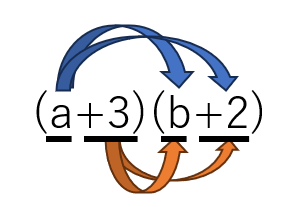
=a×b+a×2+3×b+3×2
=ab+2a+3b+6

(2)

(a+3)(a-2)

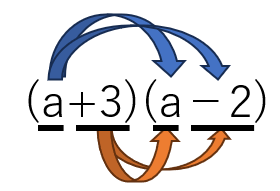
=a×a+a×(-2)+3×a+3×(-2)

=a²-2a+3a-6 ←-2a+3aが計算できるよ。

=a²+a-6

(3)

(3a-1)(2a+4)

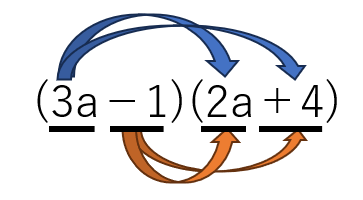
=3a×2a+3a×4-1×2a-1×4

=6a²+12a-2a-4 ←12a-2aが計算できるよ。

=6a²+10a-4

「展開する」とは？

中学３年生の数学では、「展開する」という言葉がこれからよくでてくるよ。

「展開する」とは、「多項式の積を1つの多項式で表すこと」。

簡単に言ってしまえば、分配法則なんかを使って、「かっこ（　）を外す」ことだと思ってもらえればOKだよ。

そう、実は今回学習したた「(a+b)(c+d)の計算」も「展開する」問題だったんだよ。

一問だけ、どんな感じで問題が出されるかを紹介するね。

さっきやった問題と同じで、

(a+3)(a-2)

=a×a+a×(-2)+3×a+3×(-2)
=a²-2a+3a-6
=a²+a-6

つまり、(a+3)(a-2)を展開すると、a²+a-6になるよ。

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。