乗法公式を利用して「いろいろな式の展開」をする方法を解説

中学３年生の数学で学習した乗法公式を利用して、いろいろな式の展開をしてみよう。

一見、乗法公式が使えなさそうな式でも、工夫をすれば使うことができるよ。

乗法公式を利用して 「いろいろな式の展開」をする方法を解説のPDF（9枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 乗法公式を利用していろいろな式を展開してみよう

乗法公式を利用していろいろな式を展開してみよう

乗法公式を使うと、多項式×多項式の展開がとても簡単に早くできるんだったよね。

でも、乗法公式は４つの形があって、それぞれその形の多項式×多項式の式でないと使うことができないんだったよね。

でも、あきらめるのはまだ早いよ。
ちょっと工夫することで、パッと見たところは「乗法公式の形と違うから、使えないや・・・」と思った式でも、使える場合があるんだ。

ここでは、「ちょっと工夫することで乗法公式が使えるパターン」を紹介するよ。

まず、「乗法公式」をもう一度確認しよう。全部で４つあって、この４つを使うことで、速く展開することができるんだったよね。

乗法公式について、「どういうものだったかな・・・？」と自身がなかったら、もう一度乗法公式について解説しているページをチェックしてね。

では、実際に乗法公式を使って、いろいろな式を展開する問題に挑戦してみよう。

(1) (2x+3)(2x+4)を展開しなさい。

パッと見ただけだと、この式は乗法公式の４つ形のどれにも当てはまらないよね。

でも、「なんか似ているなぁ」というものがあるね。
そう、乗法公式１の式「(x+a)(x+b)」だよ。
乗法公式の「ｘ」の部分が、問題では「２ｘ」になっているだけだからね。

この式だったら、乗法公式１の「(x+a)(x+b)=x²+(a+b)x+ab」を工夫して使えば、簡単に展開できそうな気がするね。

ではどういう工夫をするかというと、

「式の一部分を、文字におきかえてしまう」んだ。

たとえば、「2x」を「A」とおきかえてみよう。

そうすると

(2x+3)(2x+4)

=(A+3)(A+4)

となるよね。

そうすると、なんと乗法公式１の「(x+a)(x+b)」と同じ形になったね。

あとはそのまま「(x+a)(x+b)=x²+(a+b)x+ab」で展開すればよさそうだね。

(A+3)(A+4)

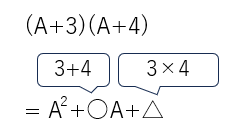
=A²+(3+4)A+3×4

=A²+7A+12

無事に展開できて、「安心！」と思ってしまいそうだけれど、
大事なことを思い出そう。

そう、「A」は仮におきかえただけの文字で、本当は「２ｘ」だったよね。

なので、最後にちゃんと「A」を「2x」に戻してあげよう。

A²+7A+12

=(2x)²+7×2x+12

=4x²+14x+12

これで展開の完成だよ。もう一度やり方を確認してみよう。

ちなみに「2x」を「A」とおいて展開する方法を紹介したけれど、展開に慣れてくると(2x+3)(2x+4)ぐらいなら、おきかえなくてもそのまま求めることもできるよ。

でも慣れないうちはミスも起こりやすいので、自身が持てるまでは、確実に展開できるように、文字でおきかえる方法でたくさん練習しよう。

(2) (2x+3)²を展開しなさい。

この式だったら、乗法公式２の「(x+a)²=x²+2ax+a²」を使えば、簡単に展開できそうな気がするね。

(x+a)²みたいな「(前+後)²」の形の式を展開すると

「前の２乗＋後ろの２乗＋２倍の前後」になるんだったよね。

(2x+3)²の展開

・前の２乗=(2x)²=4x²

・後ろの２乗=3²=9

・２倍の前後=2×(2x)×3=12x

(2x+3)²を展開すると次のようになるよ。

(2x+3)²

=4x²+9+12x ←「9」と「12x」の順番を入れ替えよう。

=4x²+12x+9

(3) (3x+4)(3x-4)を展開しなさい。

この式だったら、乗法公式４の「(x+a)(x-a)=x²–a²」を使えば、簡単に展開できそうな気がするね。

「(前＋後)(前－後）」のような形になっているから、展開すると「前の２乗－後ろの２乗」になるよ。

(3x+4)(3x-4)の展開

・「前の２乗」=(3x)²=9x²

・「後ろの２乗」=4²=16

(3x+4)(3x-4)を展開すると次のようになるよ。

(3x+4)(3x-4)

=9x²-16

(4) (x+y+2)(x+y-4)を展開しなさい。

今までと違うのは、かっこの中の数字や文字が３つになっていることだね。こういうときは、３つの文字や数字を２つにすることを考えよう。

「(x+y+2)(x+y-4)」という式を見ると、どちらにも「x+y」があることがわかるかな？

この「x+y」を「A」とおいてみよう。

(x+y+2)(x+y-4)

=(A+2)(A-4)

この形にできてしまえば、あとは乗法公式１の「(x+a)(x+b)=x²+(a+b)x+ab」を使って展開すればいいよね。

(A+2)(A-4)

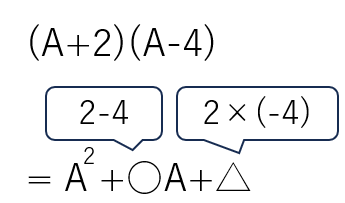
=A²+(-2+4)A+2×(-4)

=A²-2A-8

ここで「A」を「x+y」にもどすよ。

A²-2A-8

=(x+y)²-2(x+y)-8 ←(x+y)²=x²+2xy+y²となるよね。

=x²+2xy+y²-2x-2y-8

これで展開完了。このあとも計算できそうだけど、同類項がないので終わりだよ。

(5) (x+y-3)²を展開しなさい。

(4)と同じように、かっこの中の数字や文字が３つになっているね。こういうときは、３つの文字や数字を２つにすることを考えよう。

「(x+y-3)²」の「x+y」を「A」とおいてみよう。

そうすると

(x+y-3)²

=(A-3)²

になるよね。

この式だったら、乗法公式３の「(x-a)²=x²-2ax+a²」を使えば、簡単に展開できそうな気がするね。

(x-a)²みたいな「(前-後)²」の形の式を展開すると

「前の２乗＋後ろの２乗－２倍の前後」になるんだったよね。

(A-3)²の展開

・前の２乗=A²

・後ろの２乗=3²=9

・２倍の前後=2×A×3=6A

(A-3)²を展開すると次のようになるよ。

(A-3)²

=A²+9-6A ←「9」と「-6A」の順番を入れ替えるよ。

=A²-6A+9

ここまで展開出来たら、「A」を「x+y」にもどそう。

A²-6A+9

=(x+y)²-6(x+y)+9　　　　←(x+y)²=x²+2xy+y²となるよね。

=x²-2xy+y²-6x+6y+9　　

(6) (x-3)²-(x+2)(x-4)を展開しなさい。

この式は今までと比べると長くて難しそうに感じるけど、分けて考えよう。

①(x-3)²の展開

(x-a)²みたいな「(前-後)²」の形の式を展開すると

「前の２乗＋後ろの２乗－２倍の前後」になるんだったよね。

(x-3)²の展開

・前の２乗=x²

・後ろの２乗=3²=9

・２倍の前後=2×x×3=6A

(x-3)²を展開すると次のようになるよ。

(x-3)²

=x²+9-6x ←「9」と「-6x」の順番を入れ替えるよ。

=x²-6x+9

②(x+2)(x-4)の展開

乗法公式１の「(x+a)(x+b)=x²+(a+b)x+ab」を使って展開するよ。

(x+2)(x-4)

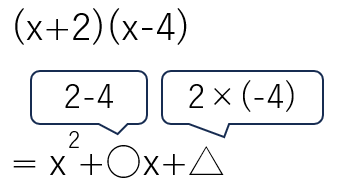
=x²+(2-4)x+2×(-4)

=x²-2x-8

③(x-3)²-(x+2)(x-4)の展開

①と②から次のように(x-3)²-(x+2)(x-4)は展開できるよ。

(x-3)²–(x+2)(x-4)

=x²-6x+9-(x²-2x-8)

=x²-6x+9-x²+2x+8

=-4x+17

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。