「円周角の定理の逆」とは?証明と問題の解き方をわかりやすく解説
中学3年生の数学で学習する「円周角の定理の逆」について、円周角の定理の逆はどうして成り立つのか、その証明方法と、円周角の定理の逆を使った問題の解き方をわかりやすく解説するよ。
円周角の定理の逆が成り立つか調べよう
「円周角の定理の逆」が成り立つのかどうか?とは、「円周角の定理」の「1つの弧に対する円周角の大きさは一定」という定理が、逆についても成り立つのかどうかということだよ。
円周角の定理の逆について勉強する前に、まずは一度「円周角の定理」とはどういうことだったかを復習しよう。
円周角の定理の復習
円周角の定理
「円周角の定理」とは次の2つのことだよ。
- 1つの弧に対する円周角の大きさは一定である。
∠APB=∠AP’B=∠AP‘‘B
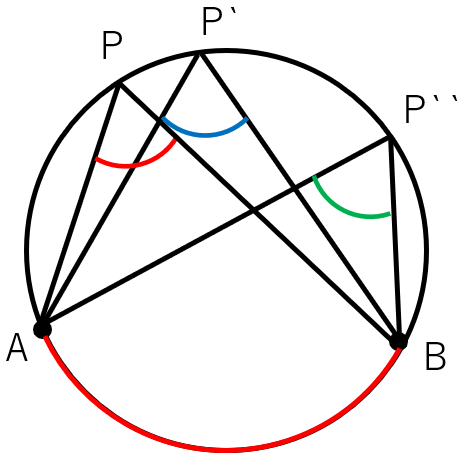
- 1つの弧に対する円周角の大きさは、その弧の中心角の大きさの半分である。
∠APB=\(\frac{1}{2}\)∠AOB
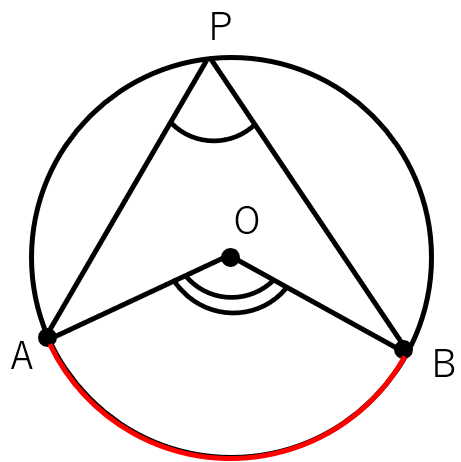
今回学習する「円周角の定理の逆」は、今復習した2つの「円周角の定理」のうち、「1つの弧に対する円周角の大きさは一定である。」という性質に注目していくよ。
∠Pと∠Cの大きさを比べよう
下の図のように、点Pが円周の上にあると、∠APB=∠ACB(∠C)になるよね。
まさにこれが「円周角の定理」の性質だよね。
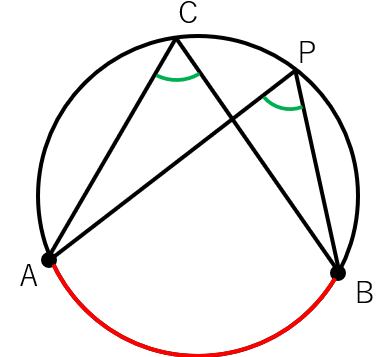
つまり、「弧ABがあり、その円周角である∠Cと∠APBは同じ角度になる」ということだね。
ここで注目して欲しいのは、
- 「弧AB」ということは、「AとBはひとつの円の円周上」にある。
- 「円周角∠C」ということは、「cは、弧ABと同じ円の円周上」にある。
- 「円周角∠APB」ということは、「Pは、弧ABと同じ円の円周上」にある。
つまり、A・B・C・Pの4点が、すべてひとつの円の円周上にあるということなんだ。
なので、円周角の定理は言い方を変えると「A・B・C・Pの4点が、すべてひとつの円の円周上にある場合、円周角である∠ACB=∠APBとなる」ということになるよ。
ここまではいいかな?
では、「円周角の定理の逆」とは、これを「逆」にしたものだよね。
つまり、「円周角である∠ACB=∠APBとなる場合、A・B・C・Pの4点が、すべてひとつの円の円周上にある」ということなんだ。
これが成り立つかどうかを、今回証明するんだよ。
これが成り立つかどうかを調べるために、点Pが、「円の外側にある場合、円周上にある場合、円の内側にある場合」の3パターンで、それぞれ∠APBと∠ACBの関係がどうなるかを確認していくよ。
点Pが円の外側にある場合
点Pが円の外側にある場合、次の図のようになるよ。
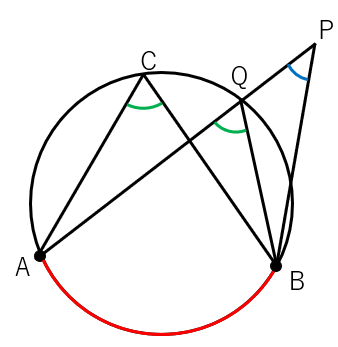
∠APBと∠Cを比較すると、∠APBは小さく見えるよね。
本当に小さいのかどうかを考えていこう。
APと円周の交点をQとして、色の付けた三角形に注目しよう。
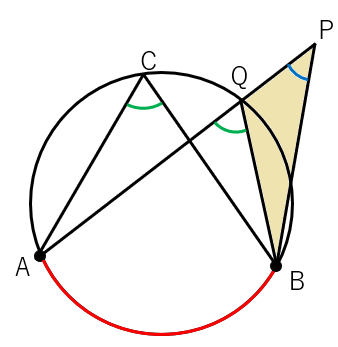
外角の性質から、
∠APB+∠PBQ=∠AQBになることがわかるよね。
円周角の定理から、
∠C=∠AQBだから、さっきの式の∠AQBのところを∠Cにすると
∠APB+∠PBQ=∠C
ということは、∠APBと∠Cを比べると∠APBの方が小さくなることがわかるね。だって、∠APBに∠PBQを足してやっと∠Cになるんだからね。
見た目だけでなく、証明からも「円周の外側にある∠APBは円周の角(∠Cや∠AQB)に比べて小さくなる」ことがわかるよね。
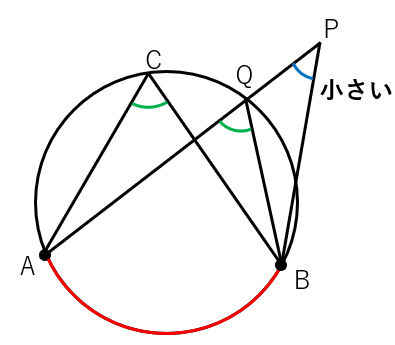
ここで分かった重要ポイントは、「点Pが円の外側にある場合、∠APBは∠C(∠ACB)よりも小さくなる」ということだよ。
点Pが円の内側にある場合
それでは次に点Pが円の内側にある場合を考えてみよう。
図にあらわすと次のようになるよ。
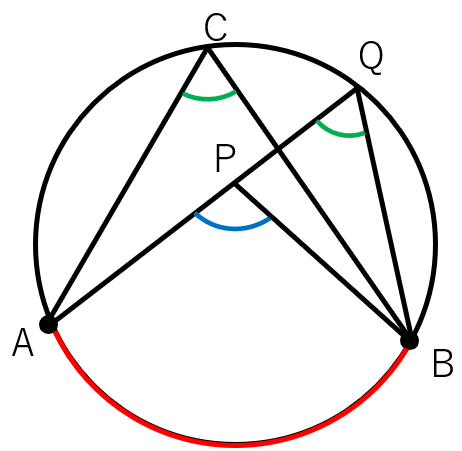
∠APBと∠Cを比較すると、∠APBは大きく見えるよね。
実際に大きいのかどうか考えていこう。
APと円周の交点をQとして、色の付けた三角形に注目しよう。
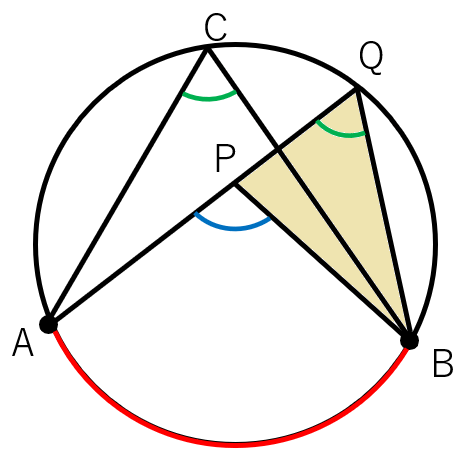
外角の性質から、
∠AQB+∠PBQ=∠APBになることがわかるよね。
円周角の定理から、
∠C=∠AQBだから、さっきの式の∠AQBのところを∠Cにすると
∠C+∠PBQ=∠APB
ということは、∠APBと∠Cを比べると∠APBの方が大きくなることがわかるね。だって、∠Cにさらに∠PBQを足して∠APBになっているからね。
見た目だけでなく、証明からも「円周の内側にある∠APBは円周の角(∠Cや∠AQB)に比べて大きくなる」ことがわかるよね。
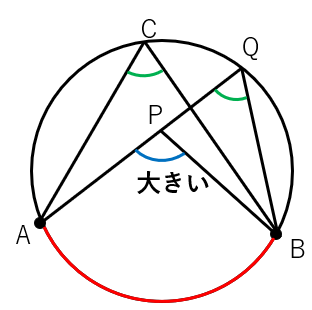
ここで分かった重要ポイントは、「点Pが円の内側にある場合、∠APBは∠C(∠ACB)より大きくなる」ということだよ。
ということは、点Pが円の外側にあっても、内側にあっても、どちらも∠APBは∠Cと同じにはならないことが分かったね。
つまり、「∠APBが∠Cと同じになるということは、点Pは円の円周上にある!」ということが言い切れるんだよ。
点Pの位置と角の大きさの関係(まとめ)
点Pの位置と角の大きさの関係をまとめるよ。
- 点Pが円周より外側にある場合、∠APBは∠ACBより小さい
- 点Pが円周より内側にある場合、∠APBは∠ACBより大きい
- 点Pが円周上にある場合、∠APBは∠ACBと等しい(円周角の定理)
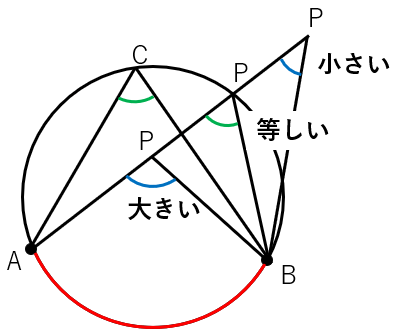
つまり、∠APB=∠ACBなのであれば、A・B・C・Pは同じ円の円周上にあるということが成り立つんだよ。
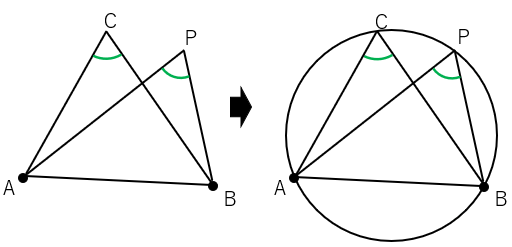
円周角の定理の逆
「円周角の定理の逆」の性質は次のようにまとめることができるよ。
4点A、B、C、Pについて、CとPが同じ側にあって、
∠C=∠Pならば、
4点は1つの円周上にある
円周角の定理の逆を使った問題
それでは、「円周角の定理の逆」を使った問題にチャレンジしてみよう。
下の図の4点A、B、C、Dは1つの円周上にあることを説明しなさい。
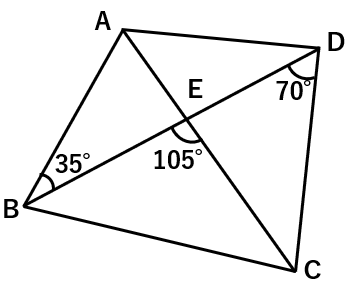
まず∠ACDの角度を求めてみよう。
色のついた三角形に注目して、外角の性質を使うと、
70+∠ACD=105になるから、
∠ACD=35°と求まるよ。
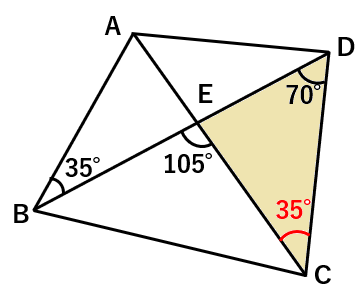
2点BとCは、ADに対して同じ側にあり、∠ABD=∠ACD=35°であるから、4点A、B、C、Dは同じ円周上にあることがわかるよ。
「円周角の定理の逆」まとめ
円周角の定理の逆
4点A、B、C、Pについて、CとPが同じ側にあって、
∠C=∠Pならば、
4点は1つの円周上にある

運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。


