相似の中心・相似の位置とは?「相似な図形の描き方」を徹底解説
中学3年生の数学で学習する「相似な図形の描き方」について、「相似の中心」・「相似の位置」とはなにか、図で表しながらわかりやすく解説するよ。
「相似の中心」とは
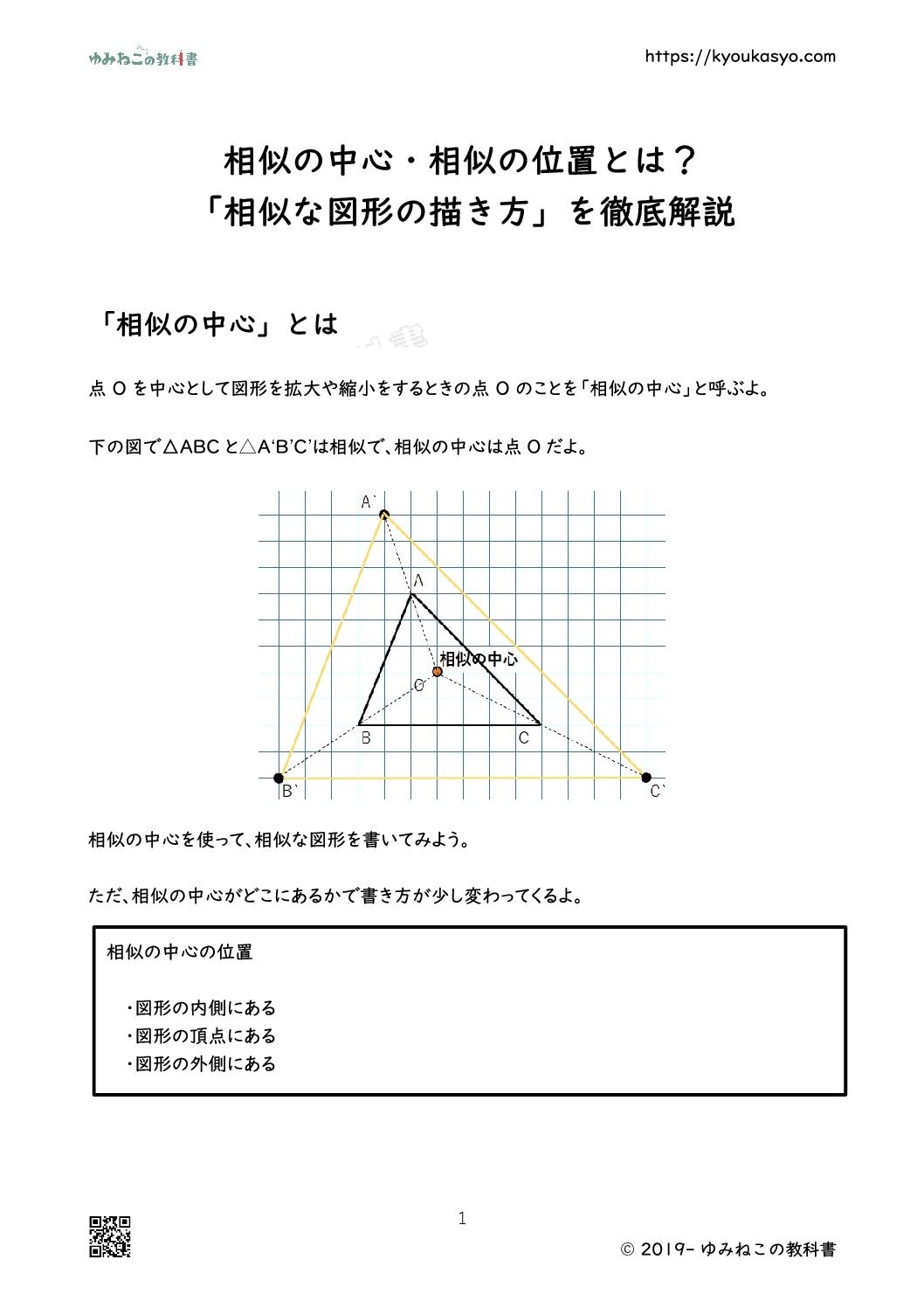
点 O を中心として図形を拡大や縮小をするときの点 O のことを「相似の中心」と呼ぶよ。
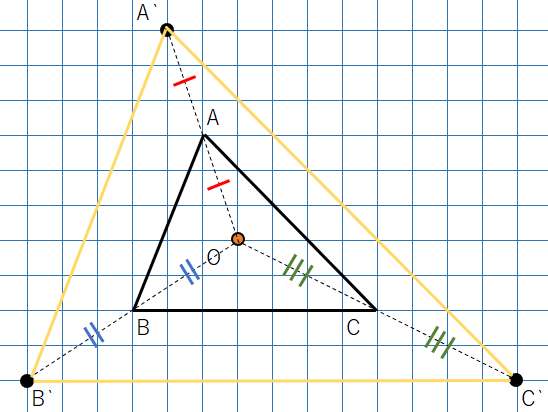
下の図で△ABCと△A‘B’C’は相似で、相似の中心は点Oだよ。
相似の中心を使って、相似な図形を書いてみよう。
ただ、相似の中心がどこにあるかで書き方が少し変わってくるよ。
相似の中心の位置
- 図形の内側にある
- 図形の頂点にある
- 図形の外側にある
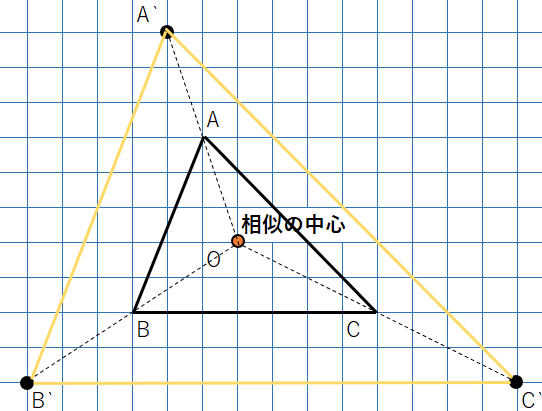
相似の中心が図形の内側にある場合
次の△ABCを点Oを相似の中心に2倍に拡大した△A’B’C’を作図しなさい。
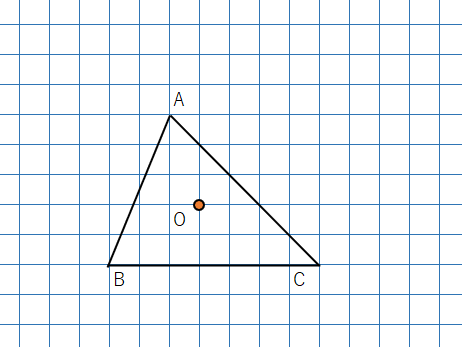
①OA、OB、OCを結ぼう。
②2倍に拡大した三角形を書くので、
- OAを延長して、OAの2倍の長さの位置にA’
- OBを延長して、OBの2倍の長さの位置にB‘
- OCを延長して、OCの2倍の長さの位置にC’
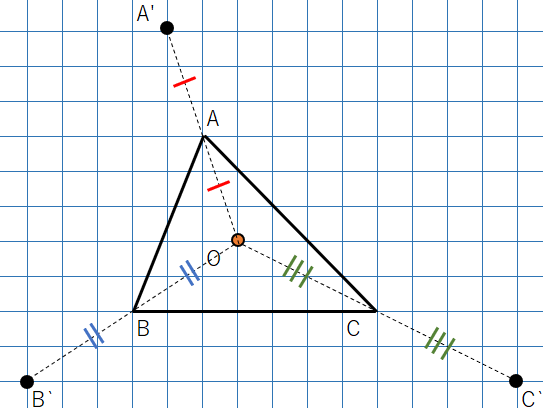
③A’B’C’を結べば、△ABCを点Oを相似の中心として2倍した△A’B’C’の完成。
相似の中心が図形の頂点にある場合
次の△ABCを点Oを相似の中心に2倍に拡大した△A’BC’を作図しなさい。
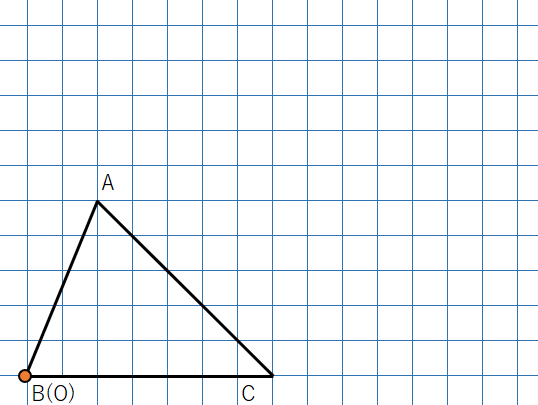
さっきの「相似の中心が図形の内側にある場合」と違うのは、相似の中心図形の頂点(この場合は点B)にあること。
それ以降の流れは同じだよ。
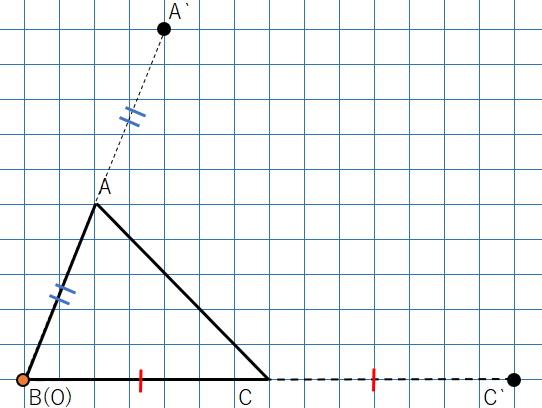
①OA、OCを結ぼう。
②2倍に拡大した三角形を書くので、
- OAを延長して、OAの2倍の長さの位置にA’
- OCを延長して、OCの2倍の長さの位置にC’
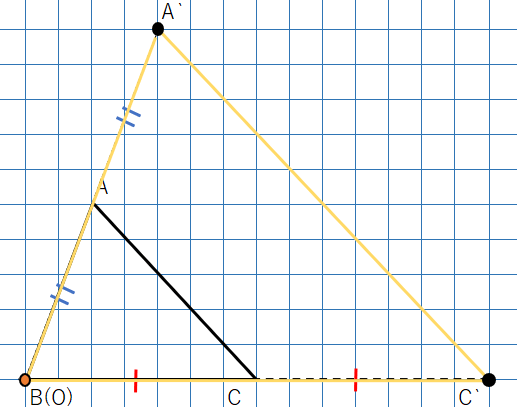
③A’BC’を結べば、△ABCを点Oを相似の中心として2倍した△A’BC’の完成。
相似の中心が図形の外側にある場合
次の△ABCを点Oを相似の中心に2倍に拡大した△A’B’C’を作図しなさい。
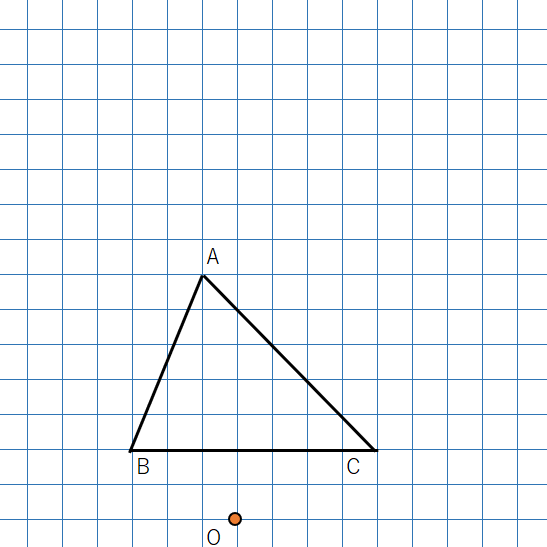
点Oが図形の外側にあっても、「点Oが図形の内部にある場合」と描き方は変わらないよ。
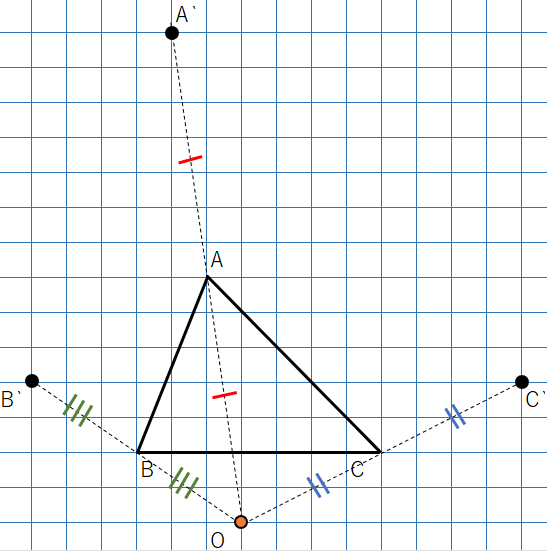
①OA、OB、OCを結ぼう。
②2倍に拡大した三角形を書くので、
- OAを延長して、OAの2倍の長さの位置にA’
- OBを延長して、OBの2倍の長さの位置にB‘
- OCを延長して、OCの2倍の長さの位置にC’
③A’B’C’を結べば、△ABCを点Oを相似の中心として2倍した△A’B’C’の完成。
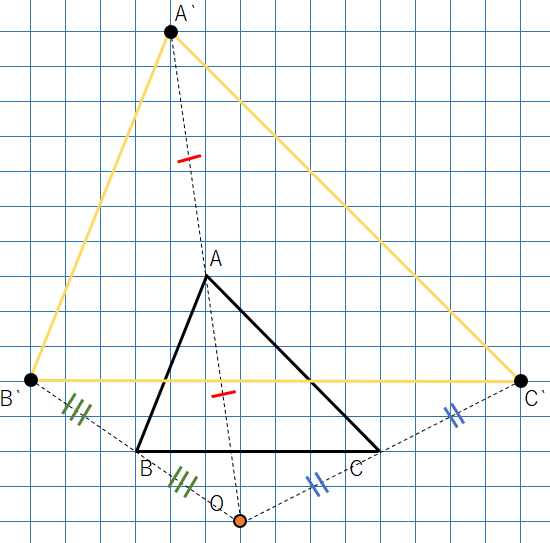
相似の中心を使って◇倍の相似な図形を書く方法
- 相似の中心Oと点ABC(それぞれの頂点)を結ぶ
- OA、OB、OCを延長して、◇倍の位置に点A’B’C’をとる
- 点A’B’C’を結ぶ
「相似の位置にある」とは
「相似の位置にある」というのは、「2つの図形が相似である」ということなんだけれど、そう呼ぶためには一応条件があるんだ。
「相似の位置にある」と呼ぶための条件
- 2つの図形の対応する点を結んだ直線が1点Oで交わる
- Oから対応する点までの距離の比がすべて等しい
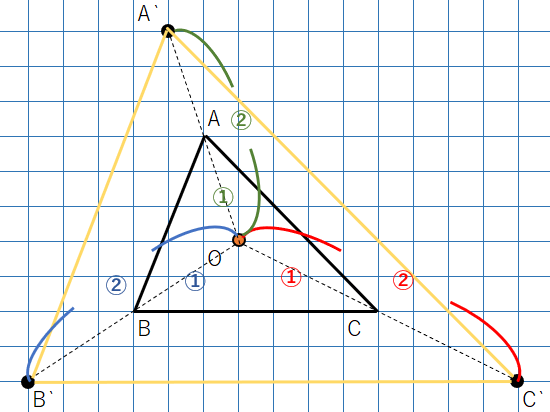
△ABCと△A’B’C’を見てみよう。
2つの図形の対応する点を結んだ直線AA’、BB’、CC’は1点Oで交わっているよね。
Oから対応する点までの距離の比を考えよう。
- OA:OA’=1:2
- OB:OB’=1:2
- OC:OC’=1:2
→距離の比はすべて1:2になっているよ。
相似の位置にあるっていう条件をクリアしているから、2つの三角形は相似の位置にあると言えるんだよ。
相似な図形の辺の長さ
相似な図形の辺の長さを求めてみよう。試験にもよく出る内容だからしっかり理解した方がいいよ。
まず相似な図形の性質を復習しよう。
相似な図形の性質
辺の長さ
→相似な図形の対応する辺の長さの比はすべて等しい。
→対応する辺の長さの比のことを「相似比」。下の図形なら1:2。
角の大きさ
→相似な図形の対応する角の大きさはそれぞれ等しい。
この性質を使って、次の問題に挑戦しよう。
下の図で△ABC∽△DEFであるとき、辺DFの長さを求めなさい。
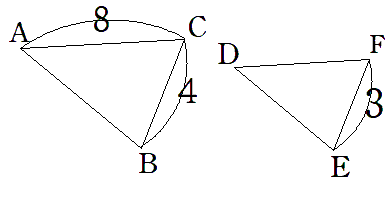
2つの図形の辺の比(相似比)を考えよう。
BCとEFが対応するから
BC:EF=4:3
相似比が4:3ってことは対応する辺の比がすべて4:3になるってことだよ。
- AC:DF=4:3
- AB:DE=4:3
- BC:EF=4:3
今回は辺DFの長さを求めたいから、xと置くと、
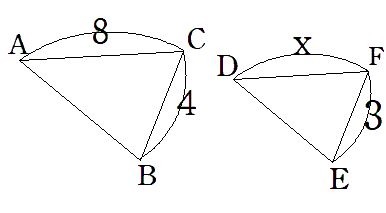
AC:DF=8:x=4:3という比例式が作れるよね。
比例式を解いていくと、
8:x=4:3 ←比例式の性質を使うよ
4×x=8×3
4x=24 ←両辺を4で割るよ
x=6
と求まるから、DFの長さは6になるよ。
比例式の性質を忘れている人は下の性質を復習しておこう。
比例式の性質
a:b=c:dならばa×d=b×c
「外側かけたもの」と「内側かけたもの」が等しい
「相似の位置」まとめ
点 O を中心として図形を拡大や縮小をするときの点 O のことを「相似の中心」と呼ぶ
相似の中心の位置
- 図形の内側にある
- 図形の頂点にある
- 図形の外側にある
相似の中心を使って◇倍の相似な図形を書く方法
- 相似の中心Oと点ABC(それぞれの頂点)を結ぶ
- OA、OB、OCを延長して、◇倍の位置に点A’B’C’をとる
- 点A’B’C’を結ぶ
「相似の位置にある」ための条件
- 2つの図形の対応する点を結んだ直線が1点Oで交わる
- Oから対応する点までの距離の比がすべて等しい
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。