「符号のついた数」をわかりやすく解説(期末テスト対策ポイント)
このページでは、中学数学「正の数・負の数」を学習するときに登場する「符号」というものが何かを解説するよ!
学習する理由!
- 中学の数学はマイナスの世界まで広がるため
- それぞれの数字が表す状態を、分かりやすくまとめるため!
「符号のついた数」
教科書にはなんて書いてあるの?
また、0℃を基準にしたとき、それよりも4℃低い温度のことを「−4℃」と表し、「マイナス4℃」と読む。 このように「+」や「−」の記号を使うとき、「+」のことを「正の符号」、「−」のことを「負の符号」と呼ぶ。
「+」や「−」はもう小学校の算数でも使ってきたけど・・それとは違うものっていうこと?
小学校の「+」と「−」とは、何が違うの??
ザックリいうと
小学校までは「計算の方法」のこと。
中学校からは「その数字がどんな状態かを表すマーク」にもなる!
小学校の「+」は「たし算」という意味で使ってきたよね。同じように、「−」は「ひき算」のことだったね。
つまり、今までの「+」や「−」は、計算の方法のことだったんだ。
例えば、「\(5-3\)」という式に登場している「−」は、「5から3を引く」という、計算の方法を伝えるためのもの。
今から学習する「+」と「−」は、「その数字がどんなものか」を表すためのマークのようなものなんだ。
数字がどんなものか・・?
符号を勉強する理由①
中学からはマイナスの世界が登場する!
次の計算をしてみよう。
\(5-3=\)?
\(5-5=\)?
\(5-3=2\)。
\(5-5=0\)だね。
では、
\(5-7=\)?
は計算できるかな?
えっ
7は5よりも大きい数だから、引けないよ
そうなんだ。
小学校では、ある数から、それよりも大きい数を引く、という考え方はしてこなかったね。
でも、中学になると、「マイナスの世界」が加わるので、こういう計算もできるようになるんだ。
例えばロールプレイングゲームなんかだと、主人公のヒットポイントが0になったらゲームオーバーだよね。

これが小学校までの算数のイメージ。
中学では、ヒットポイント以上のダメージを受けても、0よりも先の「マイナスの世界」で続けることができるんだ。

「正の数」と「負の数」
小学校まで使ってきた、「0よりも大きい数」のことを「正の数」と呼ぶよ。
そして、これから中学で使うようになる「マイナスの世界の数」、つまり「0よりも小さい数」のことを「負の数」と呼ぶんだ。
その数字が「正の数」なのか、「負の数」なのかを見分けるために、「+」と「−」をマークのように使うんだよ。
0よりも5大きい数→
「正の数」なので「\(+5\)」と書く
0よりも5小さい数→
「負の数」なので「\(-5\)」と書く
0は、「正の数」「負の数」
どちらでもないよ。
※なぜかは、この後くわしく説明するね!
- \(5-7\)のように、「ある数よりも大きい数」を引くことができるようになる!
- 「0よりも小さい数」を、符号をつけて表すことができるようになる!
こういう問題が出る!
実際の問題は、こういう風に出てくるよ
次の数を、+・−の符号を使って表しなさい。
①0よりも8小さい数
②0よりも7大きい数
③0よりも\(\frac{5}{8}\)小さい数
④0よりも0.25大きい数
① 0よりも8小さいということは、「負の数」だね。
なので、「–」の符号を使って「\(–8\)」が正解。
② 0よりも7大きいということは、「正の数」だね。
なので、「+」の符号を使って「\(+7\)」が正解。
③0よりも\(\frac{5}{8}\)小さいということは、「負の数」だね。
なので、「–」の符号を使って「–\(\frac{5}{8}\)」が正解。
④0よりも0.25大きいということは、「正の数」だね。
なので、「+」の符号を使って「\(+0.25\)」が正解。
分数や小数でも、0より大きいか小さいかで「+」と「−」の符号を前につけてあげればいいだけなんだね。
符号を勉強する理由②
反対の方向をもつ数字を、「線の上」で表す
ザックリいうと
それぞれの数字がどういうことを表しているか、分かりやすくまとめる!
例えば、こんなアンケートとか見たことはないかな?
Q:算数は好きか嫌いか、当てはまるところに○をつけよう
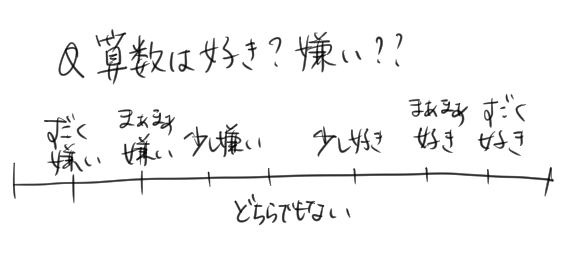
これって、真ん中は「どちらでもない」で、右にいくほど「好き」ということを表していて、左にいくほど「嫌い」を表しているんだよね。
これを、「+」と「−」を使って表すとこうなるよ。
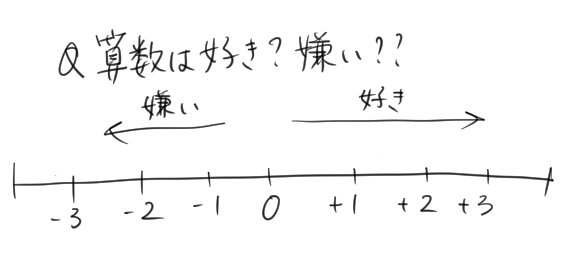
なるほど、「+」は「好き」ということを表していて、「−」は「嫌い」ということを表しているんだね。
分かりやすくなるね。
ここでのポイントは、「真ん中」を基準に、右と左が「反対の性質」や「反対の方向」を表すということだよ。
反対の性質とは
「やさしい」と「怖い」とか、
「甘い」と「苦い」とか、
「カンタン」と「難しい」とか・・
反対の方向とは、
「東」と「西」とか
「上」と「下」とか・・
さっき、「0は正の数でも負の数でもない」と説明したよね。
このように、「0」というのはつまり「真ん中」ということなので、「どちらでもない」ということを表すからなんだよ。
こういう問題が出る!
次の数量を、正の符号・負の符号を使って表しなさい。
①今の時間を基準にして、今から10分後を「\(+10\)」と表すとき、今から15分前
②今いる場所を基準にして、西へ5㎞進むことを「\(–5\)」と表すとき、東へ4㎞進むこと
③中辛のカレーを基準にして、3段階辛いカレーを「\(+3\)と表すとき、2段階甘いカレー
④平均点が65点の算数のテストで、80点を「\(+15\)」と表すとき、55点
① 今の時間が基準だから、今の時間を0とするんだね。
今よりも進んだ時間の「10分後」が正の数になっているので、今よりもさかのぼった時間の「15分前」は負の数であらわせばいいね。
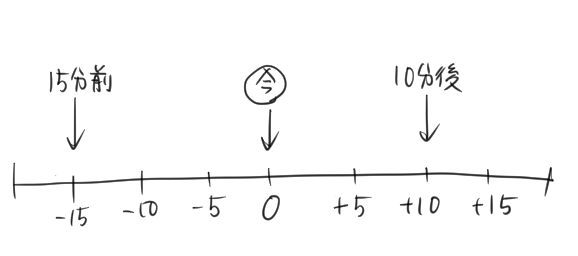
答え:\(–15\)
② 今いる場所が0だね。
西へ進むことを負の数で表しているから、反対の東へ進むことを正の数で表せばいいね。
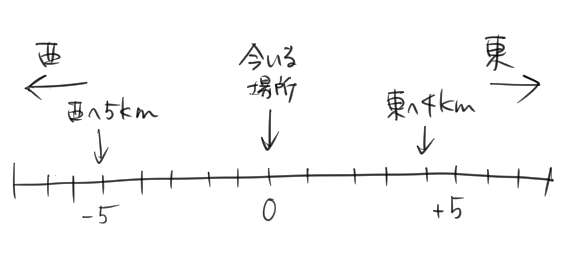
答え:\(+4\)
③ 中辛、つまり「真ん中」の辛さが0だね。
中辛よりも辛いことを正の数で表しているから、甘いことは負の数で表せばいいね。
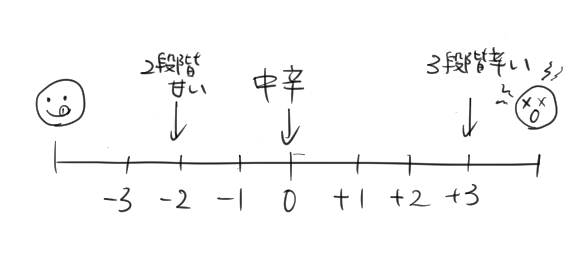
答え:\(–2\)
④ 平均点を基準にして、どのくらい大きいか少ないかで考えればいいね。
このように、基準はいつも「0」とは限らないので注意。
80点は平均点の65点よりも15点大きいね。だから正の数で表しているのだから、平均点よりも10点少ない55点は、負の数で表せばいいね。
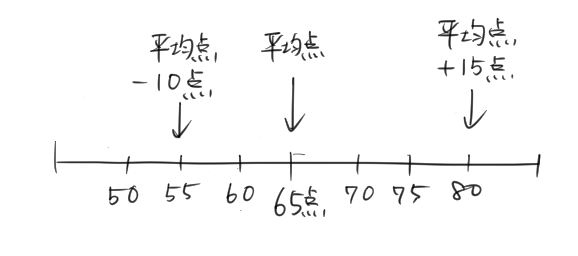
答え:\(–10\)
自然数とは?
この「正負の数」の学習では、ひとつ新しい言葉を覚える必要があるよ。
それが自然数。
自然数とは、ヒトコトで言うと
「正の整数」のこと。
整数とは?
整数というのは、小数や分数ではない数のこと。
詳しく言うと、「0と、0に1ずつ足していって出来る数または、0から1ずつ引いていって出来る数」のことなんだ。
例えば、0に1ずつ足して出来る数は
1(0+1)
2(0+1+1)
3(0+1+1+1)・・・
0から1ずつ引いていって出来る数は
−1(0ー1)
−2(0−1−1)
−3(0−1−1−1)・・・
小数の0.5とか、分数の\(\frac{3}{4}\)とかは、0に1を足したり引いたりすることでは絶対に作ることができないね。
だから整数ではないんだね。
そうだね。
ということは、整数は
0、1、2、3・・・さらに負の数の−1、−2、−3・・・ということだね。
自然数は「正の整数」って?
どこまで当てはまる?
自然数は、「正の整数」なんだよね。
さっきの「整数」に、さらに「正の数であること」という条件が加わるんだ。
−1、−2、−3・・・はもちろん
「負の数」なので、整数だけど、自然数ではないんだ。
0はどうかな?
0は「正の数」でも「負の数」でもなかったね・・!
そう。
つまり、0も自然数ではないんだよ。
この「0は自然数ではない」ということは、ついつい勘違いしてしまいがちで、
テストでもよく引っかけとして出てくるから注意。
「0が自然数かどうか」を思い出しやすいように解説したページがあるので、ぜひチェックしてね!
中学数学ではココを押さえればOK!
符号のついた数まとめ
- 0よりも大きい数のことを「正の数」といい、「+3」や「+5」のように表すことがある。
- +(プラス)のことを、「正の符号」と呼ぶ。
- 0よりも小さい数のことを「負の数」といい、「−3」や「−5」のように表すことがある。
- −(マイナス)のことを、「負の符号」と呼ぶ。
- 反対の性質や方向をもつ数量は、基準を決めることで一方を正の符号、もう片方を負の符号で表すことができる。
- 数量を表すとき、基準になる数量は0だけとは限らない。テストの平均点のように、0ではない数量を基準にしてもよい。
- 正の整数のことを、「自然数」と呼ぶ。
- 自然数に、0は含まれない。
次は「数直線」について解説するよ!
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。

-
-
とても分かりやすく書いてくださりありがとうございます
-
自学の参考にさせていただきました。ありがとうございます。
-
自学の参考にさせていただきました。ありがとうございます。
-
イラストなどが程よくかかれていて、素晴らしいと思います!
1つだけお願いしたいことがあるのですが、社会のさいとで、政治関係のものを作って欲しいです!








とても分かりやすく書いてくださりありがとうございます