自然数にゼロ（0）が含まれるかどうか？数学のテストではひっかけ問題としても良くでるこの問題、もう迷わなくなる簡単な覚え方を紹介します！
いつも分からなくなっちゃうんだ。
中学数学で登場する「自然数」という言葉。
この自然数とは何かを理解するのって結構難しいよね。
とくに、「0」は自然数に含まれるのかどうか、
「あれ？どっちだっけ？」となりがちじゃないかな？
なのに、これが結構テストでもよく出てくることがあるんだ。
自然数とはどんな数なのか？
そして0は自然数に含まれるのかどうか、
カードゲームに例えてわかりやすく説明するよ。
自然数とは？
カードゲームに例えて考えてみよう！
例えば、たろう君に「象のイラストのカード」と、「キリンのイラストのカード」を何枚か渡すよ。
このカードを使って、たろう君の友達のミツオ君に、
動物園に「象が何匹いるのか、キリンが何匹いるのか」を伝えて欲しいんだ。
早速スタートするよ。
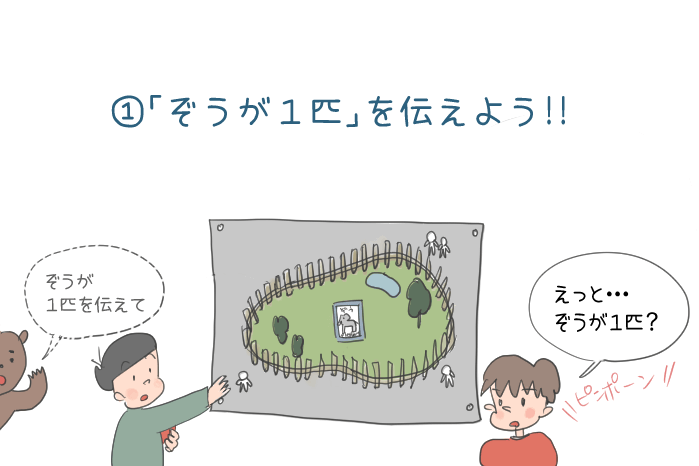
じゃあ、「象が1匹いる」を伝えてみて。
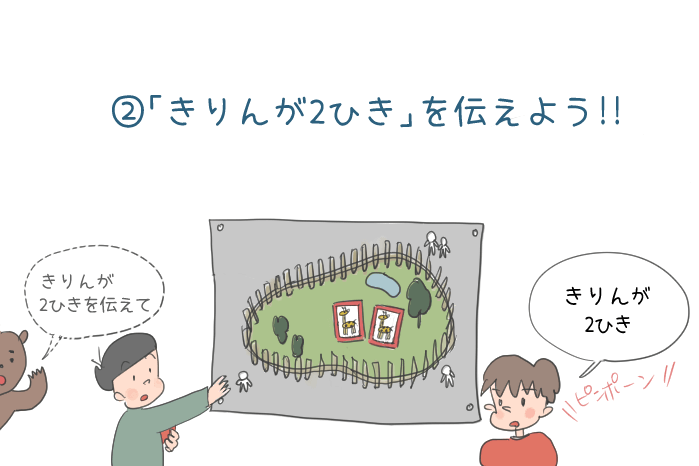
じゃあ、今度は「キリンが2匹いる」を伝えてみて。
じゃあ、「象が2匹、キリンが1匹いる」と伝えてみて。
カンタンだよ。
じゃあ、今度は「象がゼロ匹」ということを伝えられるかな？
太郎くんも、説明のしようがないよね。
じゃあ「キリンがマイナス1匹」は伝えられるかな？
そう、こうやってカードで「他の人に伝えられない数」なら、それは「自然数」じゃないということだよ。
そもそも、自然数というのは、何かを数えるためとか、順番を数えるために生まれた数字なんだ。
ということは、そこに「何かがある」から数える必要があるわけで、
なにも「ない」、つまり「0」はそもそも「数える」という考え方にならないよね。
「ない」ものを「数える」というのは、自然ではないよね。
そもそも、「自然」ってどういう意味？？
自然とは、「人の手を加えない」「ありのままの状態」という意味なんだ。
だから、「マイナス○匹」だって「ありのまま」だったらありえない状態だよね。
あれ？でも、「マイナス○度」という状態は実際にあるよね。
0℃も、「1気圧の時に水が氷になる温度」を基準にしただけで、「温度が無い」というわけではないしね。
つまり、「0」や「マイナス」は、人間が特別な状態を説明するために作り出した表現なんだ。だから、「自然数」ではないということだね。
まとめ
自然数に0が含まれるかどうか迷ったら
「象やキリンのイラストのカード」だけを使って、「象が0匹」という状態を説明できるかどうか考えよう！
「説明できない」ということは、「自然数」ではないということ！
