「連立方程式の利用」問題の解き方とコツ(割合・速さ・食塩水)
中学2年生の数学で学習した「連立方程式」を利用した問題の解き方を解説するよ。
定期テストや高校入試でよく出る「割合の問題」「速さの問題」「食塩水の問題」など、それぞれの問題の考え方や解き方のコツなどを詳しく説明するよ。
連立方程式の利用「割合の問題」の解き方
連立方程式の利用「割合の問題」では、主に2つのパターンが出題されやすいよ。
1つ目は、生徒人数に関する問題
もう1つは、商品の値段に関する問題
まずは、生徒人数に関する問題の解き方について、確認してみよう!
問題
A中学校の昨年の全校生徒の人数は、190人でした。今年は昨年に比べ、男子が15%減って、女子が10%増えたため、全体で6人減りました。今年の男子、女子の生徒人数は、それぞれ何人ですか。
「〇%増えた」、「〇%減った」この言葉を見ると、難しく感じて手が出ない…、という人もいるかもしれないけれど、式のパターンが決まっているんだ。
1つ目:昨年の生徒人数から作る式
2つ目:今年の生徒人数の増減から作る式
この2つで作ることを覚えておこう!
早速、解き方の確認をしよう。
①何をχ、yにするか
求めたいのは、今年の男子、女子の生徒人数なんだけれど、元にしているのは、昨年の生徒人数だよね。
だから、昨年の男子の生徒人数をχ人、女子の生徒人数をy人として考えていこう。
②「△の〇%」の表し方を確認して、男女の増えた人数・減った人数を求める
この文章問題で苦手な人が多いのは、「△の〇%」をどうやって表したらいいか…という部分なんだ。
そこでまずは、小学生の時の復習をして割合の計算を思い出してみよう!
復習
100円の10%はいくらでしょう。
考え方
手順1 %を小数に変えよう
10%を小数に変えるところからスタートするよ。
%を小数に変える時は、100で割ればOKだったね。
だから10%を小数に変えると…
10÷100=0.1
と変えることができたね。
手順2 もとにする数と手順1で求めた小数をかけ算する
もとにする数は、「△の〇%」の場合
△の部分がもとにする数になるよ。
100円の10%、だったら「100円」の部分
昨年の男子の生徒の15%、だったら「昨年の男子の生徒の人数」になるんだ。
今回の復習問題で計算してみると
100×0.1=10
となるので、「100円の10%は、10円」と求めることができるよ。
今回の問題では
「今年は昨年に比べ男子が15%減って、女子が10%増えた」と書いてあるね。
上の手順のように、「△の〇%」という書かれ方をしていないから、言い換える必要があるんだ。
「今年は昨年に比べ男子が15%」ということは、「昨年の男子の人数の15%」と考えてあげよう。
そうすると、昨年の男子の人数は①で決めたχを使うと、今年の男子の人数は
χ×0.15=0.15χ
と表すことができるね。
同じように女子の人数も考えよう。
「女子が10%増えた」ということは、「昨年の女子の人数の10%」と考えるから、今年の女子の人数は
y×0.1=0.1y
と表すことができるよ。
③式を作ってχとyを求めよう
1つ目の式は、「昨年の全校生徒の人数は、190人」の部分から作ろう。
「昨年の全校生徒の人数」というのは、「昨年の男子の人数と女子の人数を合わせた人数」ということだね。
だから、
χ+y=190
という式ができるよ。
次は、「今年は昨年に比べ、男子が15%減って、女子が10%増えたため、全体で6人減りました」の部分から式を作るよ。
②で求めたとおり、
今年減った男子の人数は、0.15χ
今年増えた女子の人数は、0.1y
だったから、これを元に
「今年の減った男子の人数と今年の増えた女子の人数を合わせると、全体で6人減った」という式を作ろう。
ちなみに、増えた場合には、数字の前にプラスを、減った場合には、数字の前にマイナスをつけよう。
そうすると式は、
-0.15χ+0.1y=-6
あとは、できた2つの式
\begin{cases} χ+y=190\\-0.15χ+0.1y=-6 \end{cases}
を解いて、χとyを求めよう。
計算
まずは、下の式を100倍して、小数を消すところからスタートしよう。
-15χ+10y=-600
となるね。
あとは上の式と見比べてχの数字をそろえて計算するね。
※もちろんyをそろえて計算してもOK!
15χ+15y=2850
+)-15χ+10y=-600
25y=2250
y=90
求めたy=90を元の式のχ+y=190に代入して、χを求めよう。
χ+90=190
χ=100
④答えを求めよう
答えは、男子100人、女子90人と書きたいけれど、実は違うんだ。
なぜなら、今回求めたχとyは、それぞれ昨年の人数だったよね。
今年の人数を求めるには、もう1つ手順が必要なんだ。
まずは、今年の男子の人数から求めよう。
問題文に「今年は昨年に比べ、男子が15%減って」と書いてあったね。
だから、
今年の男子の人数=昨年の男子の人数-昨年の男子の15%の人数
という計算が必要だよ。
昨年の男子の人数は、100人
昨年の男子の15%は、100×0.15=15人
を使うと
今年の男子の人数は、85人となるね。
今年の女子の人数も同じように求めていこう。
問題文に「女子が10%増えた」と書いてあるね。
これは男子と同じように「今年は昨年に比べ、女子が10%増えた」ということだから
今年の女子の人数=昨年の女子の人数+昨年の女子の10%の人数
という計算で求めることができるよ。
昨年の女子の人数は、90人
昨年の女子の10%は、90×0.1=9人
を使うと
今年の女子の人数は、99人となるね。
ということで、今回の問題の答えは、
今年の男子の人数85人、今年の女子の人数99人
と求めることができるよ。
改めて解き方のポイントを整理すると
連立方程式の利用「割合(生徒人数)の問題」の解き方のポイント
ポイント1.式の作り方
1つ目:昨年の生徒人数から作る式
2つ目:今年の人数の増減から作る式
ポイント2.何をχとyにするか
昨年の人数をχ、yとすることが多い
何を基準に考えているかをチェック
ポイント3.今年の人数を求める可能性あり
今年の人数を求める時に、1つ手順が必要!
χとyを求めて安心しないように注意しよう。
次は、商品の値段に関する問題について確認しよう。
問題
あるお店で、お弁当とお茶を1つずつ買いました。安売りをしていて、お弁当は定価の10%引き、お茶は定価の20%引きでした。
はらった代金の合計は528円で、定価で買うより72円安くなりました。
お弁当とお茶の定価は、それぞれ何円ですか。
生徒人数の問題と同じように、「〇%引き」という文字を見ると難しく感じるかもしれないけれど、基本的な解き方は同じだよ!
商品の値段に関する式も式を作るパターンが決まっていて、
1つ目:定価の式
2つ目:割引額に関する式
で作ることが多いので、覚えておこう!
じゃあ早速、解き方の確認をしよう。
①何をχ、yにするか
今回は求めたい「お弁当」と「お茶」の定価でOKだよ。
お弁当の定価をχ
お茶の定価をy
として式を作っていこう。
②割引後の値段を求める
生徒人数に関する問題と同じように考えるとOK!
「お弁当は定価の10%引き」とあるから、
χ×0.1=0.1χ
「お茶は定価の20%引き」とあるから、
y×0.2=0.2y
この2つの値を使って式を作っていこう!
③式を作ってχとyを求めよう
まずは、1つ目の定価の式から作ろう。
定価の式は、
お弁当の定価+お茶の定価=定価の合計
で作るんだ。
ただ、問題文の中に「定価の合計」が書かれていないから、計算する必要があるよ。
問題文に
「はらった代金の合計は528円で、定価で買うより72円安くなりました。」
と書いているから、お弁当とお茶の定価の合計は
528+72=600
となるので、定価の式は
χ+y=600
となるよ。
次に割引額に関する式を作ろう。
これも生徒人数の増減に関する問題と同じように作ればOK!
割引は「引」という文字があるから、生徒人数の減った時と同じように「マイナスをつける」と覚えておこう!
※「安くなった」も「マイナス」となるよ!
お弁当の割引した金額+お茶の割引した金額=割引額の合計
で作ろう。
②で求めた値を使うと
-0.1χ-0.2y=-72
と式を作ることができるよ。
式を作るときに、わざわざ「マイナス」をつける必要が無いんじゃない?と思った人もいるかもしれないけれど、
「割増」に関する問題が出題された時に混乱しないように、この作り方に慣れておくことをおすすめするよ!
また、割引後の値段を使った
0.9χ+0.8y=528
という式を考えた人もいるかな?
この式ももちろん正解なんだけれど、計算する時に数字が複雑になることがあるから、計算ミスに注意しよう!
④連立方程式を解いて、χとyを求めよう。
③で作った連立方程式
\begin{cases} χ+y=600\\-0.1χ-0.2y=-72 \end{cases}
を解こう。
計算
下の式を10倍すれば、OK!
χ+ y= 600
+)-χ-2y=-720
-y=-120
y=120
元の上の式に、代入してχを求めよう。
χ+120=600
χ=480
答えは、定価を求める問題だから、
お弁当の定価480円、お茶の定価120円
でOKだよ!
連立方程式の利用「割合(商品の値段)の問題」の解き方のポイント
ポイント1.式の作り方
1つ目:定価の式
2つ目:割引額に関する式
※2つ目の式は、割引後の合計金額の式でもOK!
ポイント2.何をχとyにするか
商品の定価をχ、yとすることがほとんど!
ポイント3.計算ミスに注意
商品の値段だから、分数や小数、マイナスになることはないよ。
もし答えの数値が怪しいと感じたら、式や計算のミスをしていないかを確認しよう!
連立方程式の利用「速さの問題」の解き方
連立方程式の利用「速さの問題」は、苦手としている人も多い単元だけれども、出題パターンが決まっているからどんどん問題を解いて、慣れていこう!
問題
太郎くんは9時に家を出発して、1200mはなれた公園に向かいました。はじめは分速50mで歩いていましたが、友だちとの待ち合わせ時間におくれそうになったので、途中から分速80mで走ったら、公園には9時18分に着きました。歩いた道のりと走った道のりは、それぞれ何mですか。
連立方程式の利用「速さの問題」では、
時間に関する式
距離に関する式
で式を作っていくよ。
式を作るときには、小学校で勉強した「み・は・じ」もしくは「は・じ・き」の公式も使っていくよ!
「み・は・じ」の公式の確認
道のり(み)=速さ×時間
速さ(は) =道のり÷時間
時間(じ) =道のり÷速さ
※速さの単位と道のり、時間の単位が違うときにはそのまま使うことができないので注意しよう!
それでは、今回の問題の解き方を確認しよう!
①何をχ、yにするか
今回の問題で求めたいものは、「歩いた道のりと走った道のり」だね。
歩いた道のりをχm
走った道のりをym
として、式をつくっていこう!
②問題に合わせて、図を描く
まずは、式を作る前に「図を描いて」問題について整理していくよ。
「図を描く」といっても、シンプルなものでOKだよ。
今回の問題では、こんな図になるよ。
図の描き方や注意点など
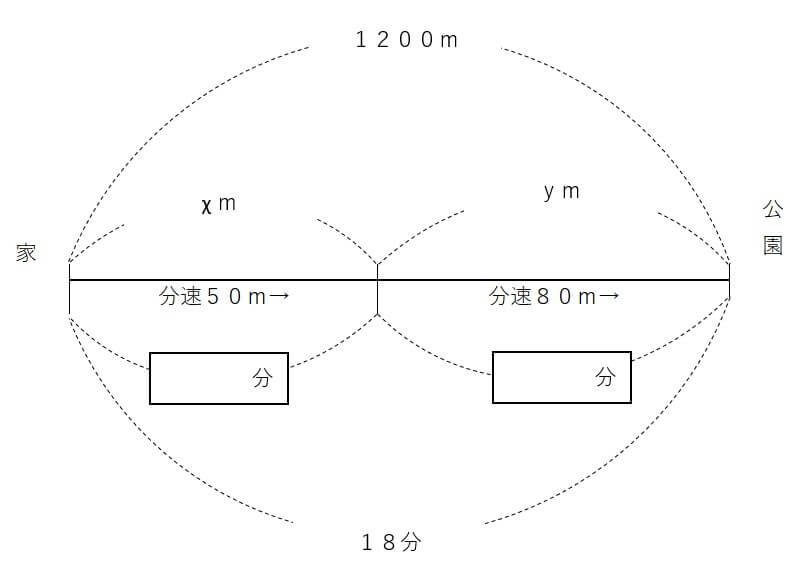
1.図に書き加える数字の位置は固定しよう
図の上側:道のり
図の真ん中:速さ
図の下側:時間
のルールで書くようにしよう。
「み・は・じ」の図では、道のりを上に、時間を下に書いているから、それと同じルールで書くとミスが少なくなるよ。
2.χ、yも含めてわかることを描き込む
このとき、必ず空欄になるところができるよ。
今回は、時間のところが空欄になるね。
3.空欄のところは、「み・は・じ」の公式を使って埋める
今回の問題では、χmの下にある時間、ymの下にある時間が空欄だね。
この空欄を埋めるには、「み・は・じ」の公式を使って埋めるよ。
χmの下にある空欄は、
道のり:χm、速さ:分速50mだから
時間=道のり÷速さに代入すると
\(\frac{χ}{50}\)分
とするんだ。
ymの下にある空欄も同じように計算すると
道のり:ym、速さ:分速80mだから
時間=\(\frac{y}{80}\)分
と埋めることができるよ。
この図を埋めたら、式は簡単に作ることができるよ。
③式を作る
まずは、図から距離で式を作ろう。
図の通りに作ればOKだから、
χ+y=1200
となるよ。
次に図の下側の時間で式を作ろう。
\(\frac{χ}{50}\)+\(\frac{y}{80}\)=18
こんな風に図から式を作れば、あとは解くだけ!
分数の計算だから、ミスがないように注意しよう!
④連立方程式を解いて、χとyを求める
③で作った2つの式
\begin{cases} χ + y = 1200 \\ \frac{χ}{50} + \frac{y}{80} = 18 \end{cases}
を使って、χとyを求めよう。
まずは、下の式の分母の数字を消すところからスタート!
両辺に400を掛けたらOKだね。
\(\frac{χ}{50}\)×400+\(\frac{y}{80}\)×400=18×400
これを整理すると
8χ+5y=7200
となるね!
あとは、もう1つの式と数を合わせて計算を進めていこう。
計算
yの前の数字をそろえて計算を進めるよ。
χ+y=1200
この式の両辺に5をかけると
5χ+5y=6000
この式ができるね!
あとは、さっき整理した
8χ+5y=7200
を使って、χとyを求めていこう!
5χ+5y=6000
-)8χ+5y=7200
↓マイナスをプラスに変えよう。式の符号を変えるのを忘れずに!
5χ+5y= 6000
+)-8χ-5y=-7200
-3χ =-1200
χ =400
元の式のχ+y=1200に代入してyを求めよう。
400+y=1200
y=800
答えは、
分速50mで歩いた距離は400m、分速80mで走った距離は800m
となるよ。
連立方程式の利用「速さの問題(どこかへ向かうパターン)」の解き方のポイント
ポイント1.必ず図を描こう
速さや道のり、時間を書いた図を描こう。
ポイント2.式のパターンは2つ
式は、
道のり+道のり=道のり
時間+時間=時間
で作ることがほとんど!
図を見て、どんな式になるか考えよう。
ポイント3.計算ミスに注意
「速さの問題」では、式が分数になることが多くあるよ。
分母を消す時に計算ミスが無いように注意しよう。
「速さの問題」では、次のパターンの問題もよくテストに出るよ!
問題
周囲が3600mの池があります。この池をAくんは自転車で、Bさんは徒歩でまわります。同じところを同時に出発して、反対の方向にまわると15分後にはじめて出会います。
また、同じ方向にまわると、AくんはBさんに30分後にはじめて追いつきます。
Aくん、Bさんのそれぞれの速さは分速何mですか。
式の作り方の確認をしよう。
2人が池の周りを反対方向にまわって、出会う時
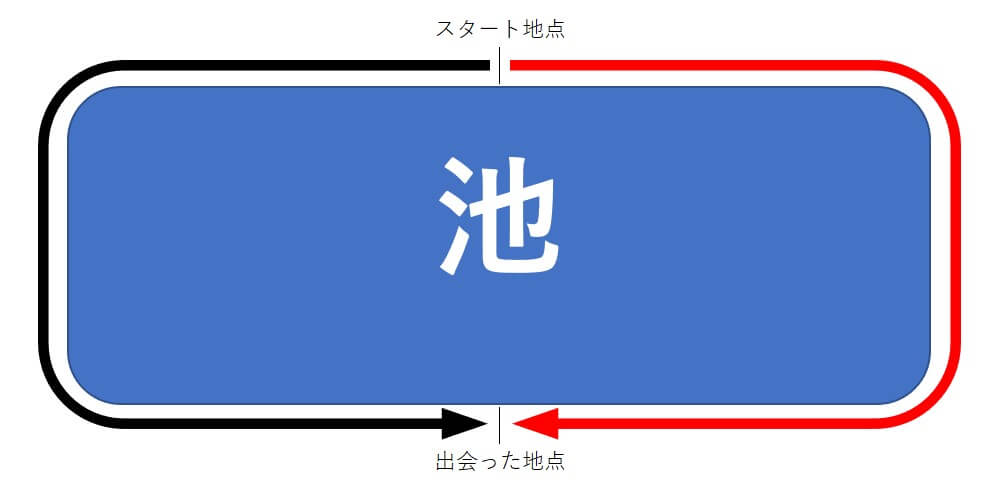
※黒い矢印はAくん、赤い矢印はBさんの進んだ道のりと考えてね。
2人の進んだ距離の合計が、池の1周分になっていることに気づくかな。
Aくんの進んだ距離+Bさんの進んだ距離=3600m
ということなんだ。
次に2人が同じ方向に進んで、AくんがBさんにはじめて追いつく時
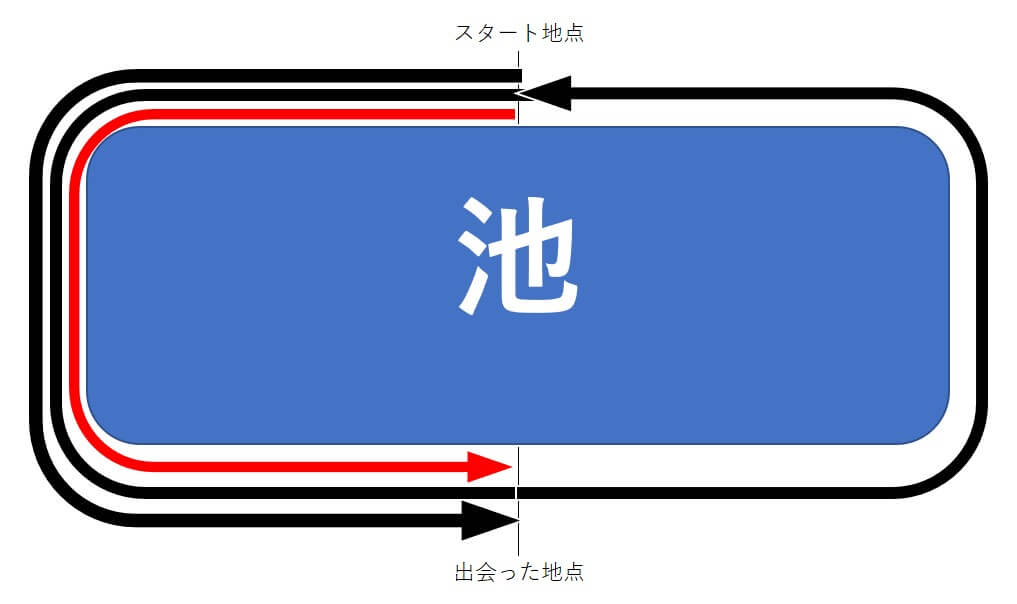
※黒い矢印はAくん、赤い矢印はBさんの進んだ道のりと考えてね。
図を見てわかる通り、Aくんが1周を差をつけてBさんと出会った、ということなんだ。
つまり
2人の進んだ距離の差が、池の1周分
Aくんの進んだ距離-Bさんの進んだ距離=3600m
ということなんだ。
ここまで確認したら、式を作っていこう!
①何をχ、yとするか
「Aくん、Bさんのそれぞれの速さは分速」を求める問題だから、
Aくんの速さ(分速)をχ
Bさんの速さ(分速)をy
とするよ。
②式を作る
まずは、「2人が池の周りを反対方向にまわって、出会う時」の式を作ろう。
Aくん、Bさんの時間、速さ、道のりを表にして確認しよう。
時間は、問題文から「15分後に出会う」とあるので、表の時間のところには、15を書くよ。
速さは、①で書いたχ、yを書こう。
道のりは、どこにも書いていないから、「み・は・じ」の公式を使って埋めるよ。
| 時間 | 速さ | 道のり(時間×速さ) | |
| Aくん | 15 | χ | 15×χ=15χ |
| Bさん | 15 | y | 15×y=15y |
ここで求められた道のりを使って、
Aくんの進んだ距離+Bさんの進んだ距離=3600m
に当てはめていこう。そうすると式は、
15χ+15y=3600
となるね!
次は、「2人が同じ方向に進んで、AくんがBさんにはじめて追いつく時」の式を作ろう。
反対向きに進んだ時と同じように、2人の進んだ距離を表を使って考えていこう。
同じ方向に進んだ時は、30分後に出会うから、それを表に書き加えよう。
| 時間 | 速さ | 道のり(時間×速さ) | |
| Aくん | 30 | χ | 30×χ=30χ |
| Bさん | 30 | y | 30×y=30y |
反対方向に進んだ時と同じように、道のりを使って
Aくんの進んだ距離-Bさんの進んだ距離=3600m
に当てはめていこう。そうすると式は、
30χ-30y=3600
となるよ。
③連立方程式を解いて、χとyを求める
②で作った式を使って、χとyを求めよう。
\begin{cases} 15χ+15y=3600\\30χ-30y=3600\end{cases}
計算
上の式を2倍して、計算をしよう。
30χ+30y=7200
+)30χ-30y=3600
60χ =10800
χ =180
これを元の式の15χ+15y=3600に代入してyを求めよう。
15×180+15y=3600
2700+15y=3600
y=60
答えは、Aくんの速さは分速180m、Bさんの速さは分速60mとなるね。
連立方程式の利用「速さの問題(池の周りを進むパターン)」の解き方のポイント
ポイント1.式のパターンは2つ
反対方向に進んで、2人が出会う場合は、
2人の進んだ距離の合計は、池の1周分
同じ方向に進んで、2人が出会う場合は、
2人の進んだ距離の差は、池の1周分
ポイント2.距離(道のり)は「み・は・じ」の公式を使うことが多い
距離=速さ×時間を使って求めよう。
※表を使って考えるとミスなくできる!
連立方程式の利用「食塩水の問題」の解き方
連立方程式の問題でよく出る問題の「食塩水の問題」にチャレンジしよう。
問題
8%の食塩水χgと3%の食塩水ygを混ぜて、6%の食塩水500gを作ろうと思います。このとき、8%の食塩水と3%の食塩水をそれぞれ何gずつ混ぜたか答えなさい。
食塩水の濃度が出てくると、理科の「質量パーセント濃度」の問題を思い出すね。
ただ、数学では濃度を求める公式は使わずに、別な公式を使うんだ。
食塩水に関する問題で使う公式だから、「食塩の公式」と呼ぶね。
食塩の公式
食塩水の中に含まれる食塩の量=食塩水×\(\frac{%}{100}\)
公式の使い方は、代入するだけだよ。
(例)
5%の食塩水200gの中に含まれる食塩の量を求める
食塩の量=200×\(\frac{5}{100}\)
=10
さあ、この公式を使ってどんな風に問題を解くか確認していこう。
①式の作り方
2つの食塩水を混ぜ合わせると、濃度は変化するけれど、変わらないものが2つあるんだ。
それは、「食塩水の量と食塩の量」だよ。
食塩水AとBを混ぜた時に、AとBの食塩水の合計よりも、できあがった食塩水の量が多くなったり、少なかったりする、ということはありえないよね。
※誰かが飲んだり、こっそり足したりする…なんてことは考えない!
食塩も同じように、食塩水A・Bの中に含まれている食塩の量が、2つを混ぜ合わせると量が増えたり減ったりはしないんだ。
この性質を使って食塩水の問題では、
食塩水+食塩水=食塩水
食塩+食塩=食塩
という式を作るんだ。
まずは、「食塩水+食塩水=食塩水」の式から作ろう。
といっても、この式はすぐに完成するよ。
今回の問題では、
8%の食塩水χg、3%の食塩水yg、6%の食塩水500g
が登場したね。
これをさっきの式に当てはめると
「8%の食塩水+3%の食塩水=6%の食塩水」
ということになるから、
χ+y=500
で完成するよ。
次に、「食塩+食塩=食塩」の式を作ろう。
この式は、「食塩の公式」を使って計算する必要があるんだ。
問題に登場した3つの食塩水の中に含まれている食塩の量を求めよう。
8%の食塩水χgの中に含まれる食塩=χ×\(\frac{8}{100}\)
=\(\frac{8}{100}\)χ
3%の食塩水ygの中に含まれる食塩=y×\(\frac{3}{100}\)
=\(\frac{3}{100}\)y
6%の食塩水500gの中に含まれる食塩=500×\(\frac{6}{100}\)
=30
これを「食塩+食塩=食塩」に当てはめると
\(\frac{8}{100}\)χ+\(\frac{3}{100}\)y=30
という式が完成するよ。
②連立方程式を解いて、χとyを求める
①で作った連立方程式
\begin{cases} χ + y = 500 \\ \frac{8}{100}χ + \frac{3}{100}y = 30 \end{cases}
を解いて、χとyを求めよう。
計算
下の式の両辺に100倍して分数を消すところからスタートしよう。
下の式の両辺を100倍すると
8χ+3y=3000
次に上の式を3倍して、yの前の数字をそろえよう。
3χ+3y=1500
ここから、それぞれをひき算して計算をしていこう。
8χ+3y=3000
-)3χ+3y=1500
↓マイナスをプラスに変えて、式の符号を変えよう。
8χ+3y= 3000
+)-3χ-3y=-1500
5χ = 1500
χ = 300
これを元の式のχ+y=500に代入してyを求めよう。
300+y=500
y=200
答えは、8%の食塩水は300g、3%の食塩水は200gとなるね。
連立方程式の利用「食塩水の問題」の解き方のポイント
ポイント1.食塩の公式をマスターしよう
食塩水の中に含まれる食塩の量=食塩水×\(\frac{%}{100}\)
ポイント2.食塩水の問題の連立方程式は、基本は2パターン
食塩水+食塩水=食塩水
食塩+食塩=食塩
この2つを使って、連立方程式を作るよ!
テストに出やすい連立方程式の文章題を一気に紹介したよ。
今回出てきた問題を繰り返し解いて、まずは式をスムーズに作るところからスタートしよう。
また、注意点として連立方程式の文章問題で、テストに式を書くときには
簡略化したり、両辺に数字をかけたりした式は書かない
というルールがあるよ。
(例)
\begin{cases} χ + y = 500 \\ \frac{8}{100}χ + \frac{3}{100}y = 30 \end{cases}
この式だと、下の式を100倍して
\begin{cases} χ + y = 500 \\ 8χ + 3y = 3000 \end{cases}
と書きたくなるかもしれないけれど、我慢我慢…。
テストで式を聞かれたら「元の式のまま書く」ということを覚えておこう!
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


