「中点連結定理」とは？三角形の中点連結定理の証明をわかりやすく解説

中学３年生の数学で学習する三角形の「中点連結定理」について、中点連結定理とはどういうことか、なぜ中点連結定理が成り立つのかを、証明する方法をくわしく解説しているよ。

「中点連結定理」とは？ 三角形の中点連結定理の証明をわかりやすく解説のPDF（6枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 中点連結定理とは
• 中点連結定理の問題
• 中点連結定理の証明問題

中点連結定理とは

「中点連結定理」とは、「三角形と比の定理」の少し特殊なバージョンだと思っておけばOKだよ。

名前の通り「中点」を「連結」させたときの性質のことだよ。
ちなみに、図形の中点を連結させたときの定理なので、今回紹介する三角形以外の図形（たとえば平行四辺形など）でも、この中点連結定理があるよ。

それでは三角形の中点連結定理について学習しよう。

三角形の場合、中点連結定理とは、下のような三角形で中点DとEを結ぶと、DE//BC、DE：BC＝１：２になるという定理だよ。

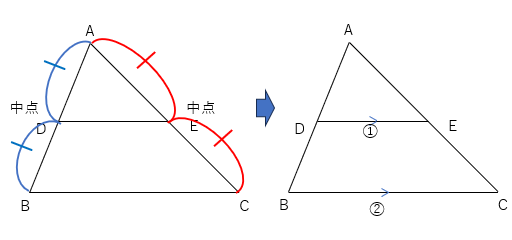
ざっくり説明すると、三角形の２つの辺のそれぞれ真ん中になる点をとって、その点どうしを結ぶと、結んだ辺と三角形の底辺は平行になる、ということだね。

さらに、その辺と三角形の底辺の比は、１：２になるんだね。

教科書には次のように載っているよ。

中点連結定理の練習問題

中点連結定理を使う問題では、辺の長さを求める問題がよく出るよ。

問題　次の図で、ｘの長さを求めなさい。

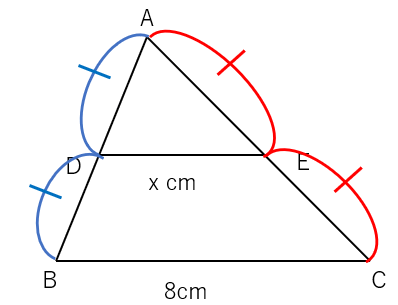
Dは辺ABの中点、Eも辺ACの中点だから、DとEを連結すると、中点連結定理が使えるね。

ということは辺DEと底辺BCの比は、１：２になるね。
なので、辺DEは底辺BC×\(\frac{１}{２}\)で求めることができるね。

DE＝\(\frac{１}{２}\)BC
DE＝\(\frac{１}{２}\)×８
DE＝４

辺DEの長さは４ｃｍと求めることができたね。

中間連結定理の証明問題

それでは、そもそもなぜ中点連結定理が成り立つのか考えてみよう。

中点連結定理とは次のような定理だったね。

中点連結定理は、中点どうしを結んだ辺と底辺が「平行になること」と、中点どうしを結んだ辺が底辺の「\(\frac{１}{２}\)になること」の２つに分かれているので、それぞれひとつずつ順番に証明していくよ。

中点どうしを結んだ辺と底辺が平行になることの証明

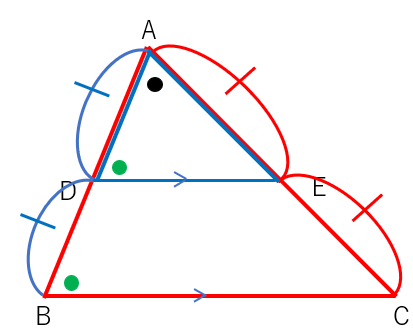
三角形の２辺の中点で連結すると、△ADEと△ABCは相似になるよ。

なぜかというと、∠Aは共通でAD：AB＝AE：AC＝１：２になって、相似条件の「２組の辺の比とその間の角がそれぞれ等しい」を満たすからだね。

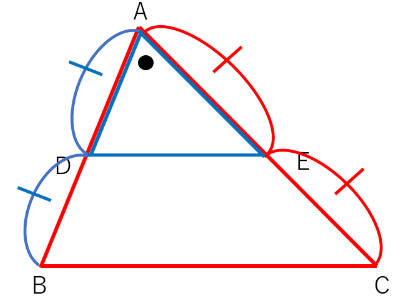
△ADEと△ABCが相似だということは、対応する角が等しくなるから
∠ADE＝∠Bになるよね。

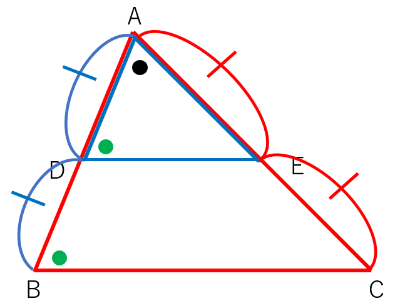
緑丸の位置は同位角の位置で、同位角の∠ADE＝∠Bが等しくなるということは、平行線の性質によりDEとBCは平行になることがわかるね。

これで、「中点どうしを結んだ辺と底辺が平行になること」の証明ができたね。

中点どうしを結んだ辺は底辺の\(\frac{１}{２}\)になることの証明

青（△ADE）と赤（△ABC）の三角形は相似になるんだったよね。

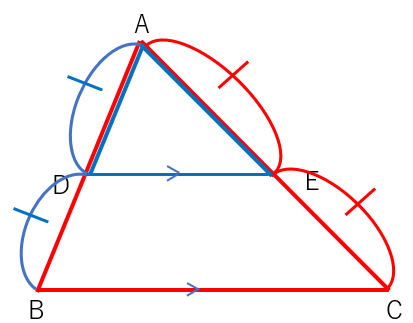
２つの三角形をわけて考えてみよう。

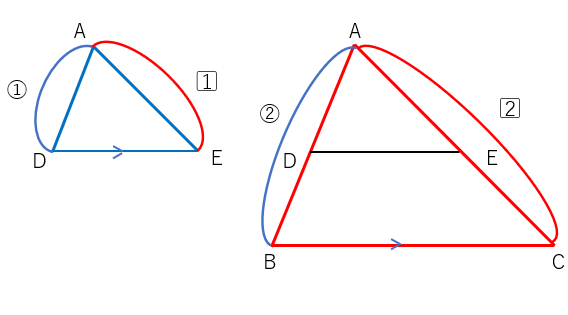
点Dは辺ABの中点、点Eは辺ACの中点だから、AD：AB＝AE：AC＝１：２になっているよね。

相似な図形の性質を思い出してみよう。

ということは、△ADEと△ABCは相似な図形なので、対応する辺の長さの比はそれぞれ等しいということだね。

AD：AB＝AE：AC＝１：２なのだから、残ったDE：BCの長さの比も１：２になるということだよね。

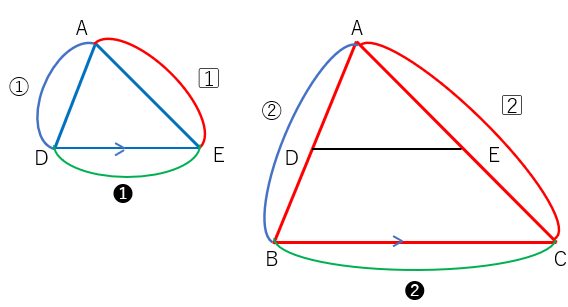
これで、「中点どうしを結んだ辺は底辺の\(\frac{１}{２}\)になること」の証明ができたね。

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。