「相似な立体の表面積と体積」を例題を使ってわかりやすく解説

中学３年生の数学で学習する「相似な立体の相似比と表面積比」、「相似な立体の相似比と体積比」について、立方体・円柱・球それぞれの場合を例題を使ってわかりやすく解説しているよ。

「相似な立体の表面積と体積」を例題を使ってわかりやすく解説のPDF（12枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

相似な立体の相似比と表面積の比を調べよう

相似な図形の相似比と面積比の関係は学習したね。
今回の単元では、「相似な立体」の場合について学習するよ。

相似な立方体の相似比と表面積の比を調べよう

まずは、「相似な立体の相似比と表面積の比」はどうなるかを調べてみよう。
立体の表面積とは、「空気に触れている部分」とイメージするとよかったよね。

相似な図形の相似比と面積比に関係があったように、相似な立体の相似比と表面積の比にも関係があるよ。

わかりやすく考えるために、次のような立方体で表面積を求めてみよう。
「立方体」はすべての辺の長さが同じだから、必ず相似な立体になるんだ。

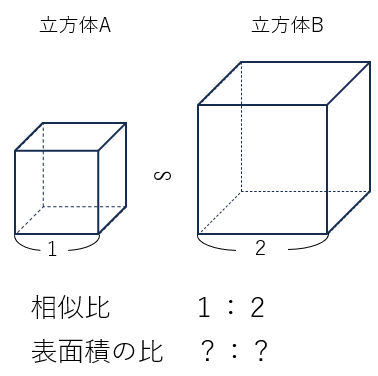
立方体Aの表面積を求めよう。

１つの正方形の面積は１×１＝１
面は６つあるので表面積は１×６＝６

立方体Bの表面積を求めよう。

１つの正方形の面積は２×２＝４
面は６つあるので表面積は４×６＝２４

表面積の比を求めよう。

立方体Aの表面積：立方体Bの表面積＝６：２４＝１：４

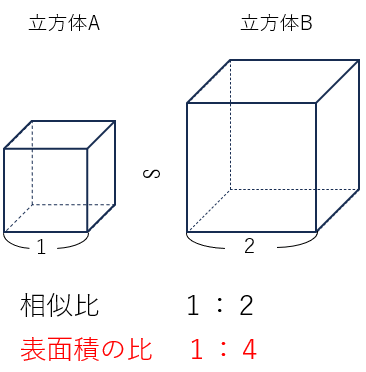
相似な立体で、相似比が１：２のとき、表面積の比は１：４＝１^２：２^２になることがわかったね。

つまり、相似な立体の表面積の比は相似比の二乗になるんだ。

相似な立体の相似比と表面積の比

相似な立体の相似比がａ：ｂであれば、
表面積の比はａ^２：ｂ^２となる。

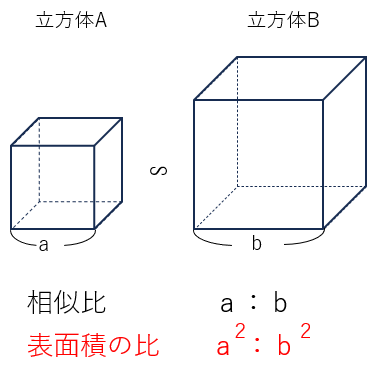
今回は「立方体」で相似比と表面積の比について調べたけれど、実は他の相似な立体でも、表面積の比は相似比の二乗になるんだよ。

相似な立体の相似比と体積の比を調べよう

では次に「相似な立体の表面積と体積の関係」を調べよう。
表面積よりも体積の比の方が問題になりやすいから、しっかり理解しよう！

相似な立方体の相似比と体積の比を調べよう。

わかりやすく考えるために、次のような立方体で体積を求めてみよう。

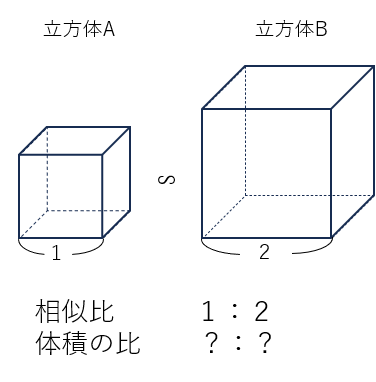
立方体の体積は（１辺）×（１辺）×（１辺）で求まるから

立方体Aの体積：立方体Bの体積
＝１×１×１　：　２×２×２
＝１：８

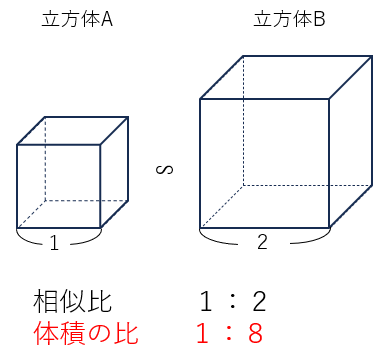
「８」を見て、あることに気づいてほしいんだけど、
「８」は２の３乗だよね。
「１」も１の３乗と考えることができるから、
体積の比は、相似比の３乗になっているよね。

相似な立体で、相似比が１：２のとき、体積の比は１：８＝１^３：２^３になることがわかったね。

つまり、立方体の体積の比は相似比の３乗になるんだよ。

相似な立方体の相似比と体積の比

相似な立方体の相似比がａ：ｂであれば、
体積の比はａ^３：ｂ^３となる。

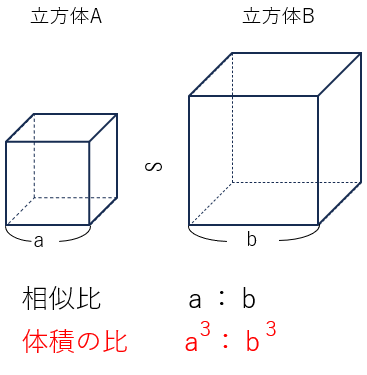
今回は「立方体」で体積の比が相似比の３乗になることがわかったね。
では、他の立体ではどうなるかを調べてみよう。

相似な円柱の相似比と体積の比を調べよう

次のような相似な円柱AとBを考えよう。円柱Aの半径３、高さ４で、円柱AとBの相似比は１：２になるよ。

このときの体積の比を求めよう。

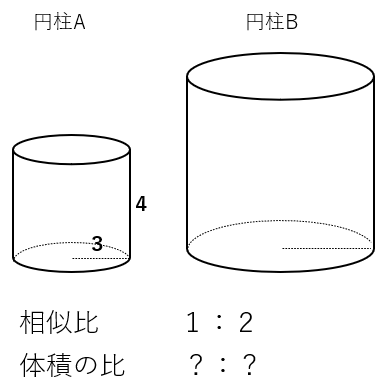
STEP１　円柱Bの底面の半径と高さを求めよう

相似比が１：２ってことは、円柱Aの長さの２倍が円柱Bの長さってことだよね。ということは、円柱Bの半径は３×２＝６、高さは４×２＝８と求まるね。

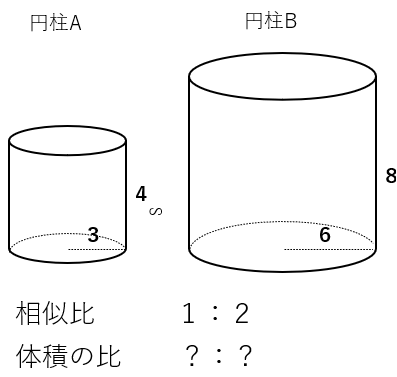
STEP２　円柱Aの体積を求めよう

円柱の体積は（底面積）×（高さ）で求まるから、円柱Aの体積は

３×３×π×４＝３６π

と求まるね。

STEP３　円柱Bの体積を求めよう

円柱Aと同じように計算すると、円柱Bの体積は

６×６×π×８＝２８８π

と求まるね

STEP４　体積の比を求めよう

円柱Aの体積：円柱Bの体積＝３６π：２８８π

になるね。

両方にπがあるから、πで割ろう

円柱Aの体積：円柱Bの体積
＝３６π：２８８π
＝３６π÷π：２８８π÷π
＝３６：２８８

両方とも３６で割ると

３６：２８８
＝３６÷３６：２８８÷３６
＝１：８

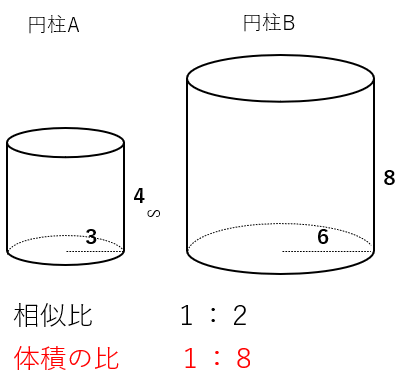
相似な円柱でも、相似比が１：２のとき、体積の比は１：８＝１^３：２^３になることがわかったね。

つまり、体積の比は相似比の３乗になるということが、円柱でも説明できたね。

相似な球の相似比と体積の比を調べよう

最後に相似な球AとBを考えよう。球Aの半径１、球Bの半径２のとき、体積の比を求めよう。

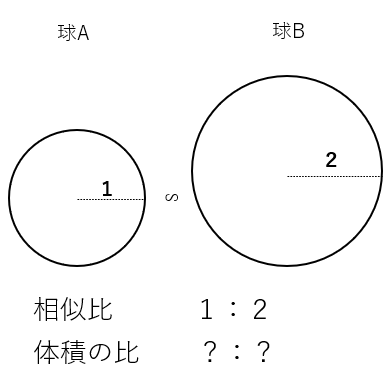
球の体積は\(\frac{４}{３}\)πｒ^３で求まるんだったよね。

「ｒ」には球の半径を代入しよう。

球Aの体積を求めよう

\(\frac{４}{３}\)πｒ^３　　　　　ｒ＝１を代入しよう
＝\(\frac{４}{３}\)π×１^３
＝\(\frac{４}{３}\)π×１
＝\(\frac{４}{３}\)π

球Bの体積を求めよう

\(\frac{４}{３}\)πｒ^３　　　　ｒ＝２を代入しよう
＝\(\frac{４}{３}\)π×２^３
＝\(\frac{４}{３}\)π×８
＝\(\frac{３２}{３}\)π

球Aと球Bの体積の比を求めよう

球Aの体積：球Bの体積＝\(\frac{４}{３}\)π：\(\frac{３２}{３}\)π

両方にπがあるから「π」で割って、分母を消すために「３」をかけよう

球Aの体積：球Bの体積
＝\(\frac{４}{３}\)π：\(\frac{３２}{３}\)π
＝４：３２　　　←８で割ろう
＝１：８

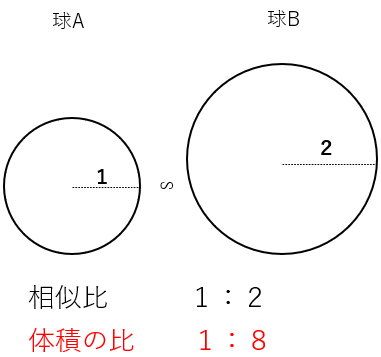
相似な球でも、相似比が１：２のとき、体積の比は１：８＝１^３：２^３になることがわかったね。

つまり、体積の比は相似比の３乗になるということが、球でも説明できたね。

相似な立体の表面積と体積の定理

相似な立体の表面積の比と体積の比には、次のような関係があるよ。
すべての相似な立体で成り立つことに注意しよう。

相似な立体の表面積と体積の定理

相似な立体では

表面積の比は相似比の２乗に等しい
相似比ａ：ｂならば、表面積の比はａ^２：ｂ^２

体積の比は相似比の３乗に等しい
相似比ａ：ｂならば、体積の比はａ^３：ｂ^３

相似な立体の表面積と体積の定理を使った問題

それでは、相似な立体の表面積と体積の定理を使った問題にチャレンジしてみよう。

次の立体Aと立体Bは相似で、相似比は３：４である。
次の問に答えなさい。
ただし、立体は直方体とする。

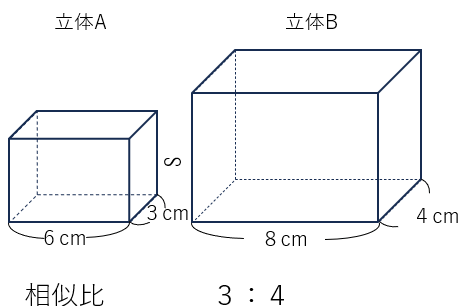
表面積の比を求めなさい。
体積の比を求めなさい。
立体Aの体積が５４cm²のとき、立体Bの体積はいくつか。
立体Bの高さを求めなさい。

問題1

表面積の比は相似比の２乗だから、３^２：４^２＝９：１６と求めることができるよ。

問題２

体積の比は相似比の３乗だから、３^３：４^３＝２７：６４と求められるよ。

問題３

立体Aの体積が５４cm²のとき、求めたい立体Bの体積をｘcm²としよう。
体積の比は２７：６４だったから、次の比例式がたてられるよ。

２７：６４＝５４：ｘ

この比例式を解いていこう。

２７：６４＝５４：ｘ
２７ｘ＝６４×５４　　　　　　　両辺を２７で割ろう
２７ｘ÷２７＝６４×５４÷２７
ｘ＝６４×２
ｘ＝１２８

立体Ｂの体積が１２８cm²と求めることができたね。

問題４

立体Bのような直方体の体積は（底面積）×（高さ）で求められるね。

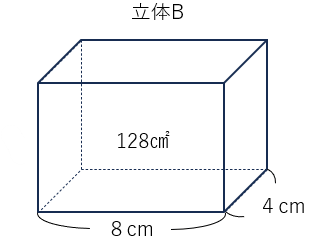
（底面積）×（高さ）＝（体積）だから

４×８×（高さ）＝１２８
３２×（高さ）＝１２８
（高さ）＝１２８÷３２＝４

高さは４cmと求めることができたね。

「相似な立体の表面積の比と体積比」まとめ