三平方の定理の問題を速く解くために覚えるべき３辺の比７パターン

中学３年生の数学で学習する「三平方の定理」について、問題を速く解くための裏ワザ「覚えるべき３辺の比の７パターン」を紹介するよ。

それぞれの比のパターンの特徴や覚え方、例題など、くわしく解説していくよ。これを覚えれば、２乗する作業や、方程式を解く作業が省略できるので、速く三平方の定理の問題を解くことができるようになるよ。

三平方の定理の問題を速く解くために覚えるべき ３辺の比７パターンのPDF（22枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 「三平方の定理」覚えるべき３辺の比７つのパターン
• 覚えるべき３辺の比が整数の直角三角形
• 覚えるべき３辺の比にルートを含む直角三角形
• まとめ

「三平方の定理」覚えるべき３辺の比７つのパターン

「三平方の定理」とは、下のような直角三角形があった時に、ａ^２＋ｂ^２＝ｃ^２となる関係のことだったよね。

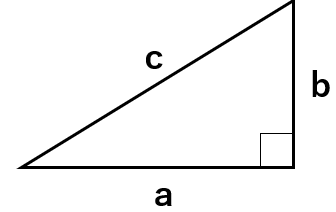
ａ、ｂ、ｃに入る数が小さいときは計算は大変じゃないんだけれど、大きくなってくると２乗の計算が大変になって、解くのに時間もかかってしまうよね。

例えば、「ａ＝８、ｂ＝１５のときｃはいくつになるかな」みたいな計算の場合、８^２＋１５^２の計算って時間がかかるよね。

そんなときに
「三平方の定理」覚えるべき３辺の比７パターン
を知っていると、２乗の計算をすることなく答えを求めることができてしまうんだ。

これから紹介する「覚えるべき３辺の比」は、もちろん覚えていなくてもなんとか計算で求められるけれど、知っていると確実に速く答えを求めることができるようになるよ。

中学生で覚えておいてほしい、三平方の定理の比の７パターンは次の通り

①～④は整数だけ、⑤～⑦はルートも入ってくるね。①～④と⑤～⑦を分けて順番に紹介していくね。

覚えるべき３辺の比が整数の直角三角形

覚えたほうがいい３辺の比がすべて整数の直角三角形は中学校では４つ学習するよ。

①～④のようなａ^２＋ｂ^２＝ｃ^２の条件を満たす、すべて自然数の組み合わせのことを「ピタゴラス数」というよ。
「三平方の定理」のことを「ピタゴラスの定理」とも呼ぶよね。
なので、「三平方の定理」の条件を満たす自然数の組み合わせの数ということで、これも「ピタゴラス数」と呼ばれるんだ。

ピタゴラス数は無限個あるよ。
④７：２４：２５以降のピタゴラス数の一部を紹介するね。

こんなに大きな数は覚える必要はないから、①～④のピタゴラス数はしっかり覚えるようにしよう。

３辺の比が３：４：５の直角三角形

覚えてほしい３辺の比の中でもっとも簡単なものだよ。

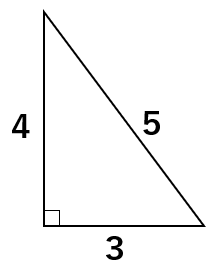
本当に３：４：５の関係が成り立つのか、三平方の定理ａ^２＋ｂ^２＝ｃ^２のａ、ｂ、ｃに数字を代入してみよう。

３、４、５のうち、最も長いものが斜辺ｃだから、ｃ＝５になるよ。

（左辺）
＝ａ^２＋ｂ^２
＝３^２＋４^２
＝９＋１６
＝２５

（右辺）
＝ｃ^２
＝５^２
＝２５

（左辺）＝（右辺）になるから、３：４：５の関係が成り立つことが分かったね。

３辺の比３：４：５を使った問題

次の直角三角形の斜辺の長さｘを求めなさい。

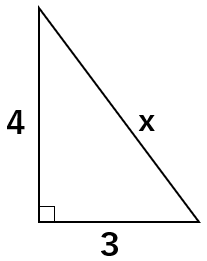
丁寧にやるのであれば、
三平方の定理ａ^２＋ｂ^２＝ｃ^２のａ、ｂに３、４を代入して
３^２＋４^２＝ｘ^２
９＋１６＝ｘ^２
ｘ^２＝２５
ｘ＝±５

と計算してもOK。

ただ直角三角形の３辺の比「３：４：５」を知っていたら、ｘ＝５と一瞬で求めることができるんだよ。

次の直角三角形の斜辺の長さｘを求めなさい。

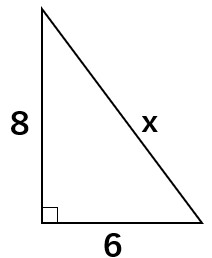
丁寧にやるのであれば、
三平方の定理ａ^２＋ｂ^２＝ｃ^２のａ、ｂに６、８を代入して
６^２＋８^２＝ｘ^２
３６＋６４＝ｘ^２
ｘ^２＝１００
ｘ＝±１０

と計算してもOK。

ただ直角三角形の３辺の比「３：４：５」だから、３つの辺の比を２倍すると「６：８：１０」になるよね。

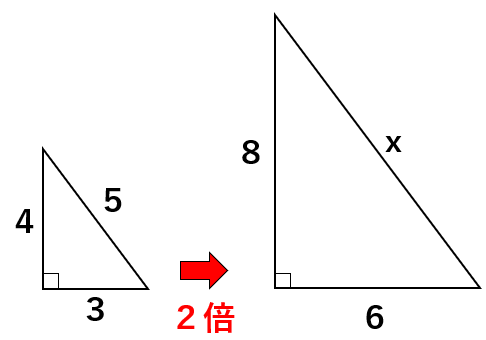
そうすると、ｘ＝１０と一瞬で求めることができるんだよ。

３辺の比が５：１２：１３の直角三角形

少し数が大きくなってきたね。１２の２乗とか１３の２乗とかを計算するのは面倒だよね。
そんなとき５：１２：１３の関係を知っていれば、２乗の計算をせずにできちゃう問題もあるよ。

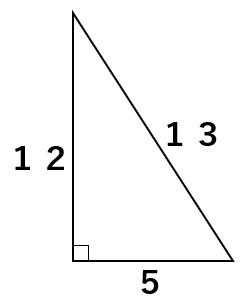
本当に５：１２：１３の関係が成り立つのか、三平方の定理ａ^２＋ｂ^２＝ｃ^２のａ、ｂ、ｃに数字を代入してみよう。

５、１２、１３のうち、最も長いものが斜辺ｃだから、ｃ＝１３になるよ。

（左辺）
＝ａ^２＋ｂ^２
＝５^２＋１２^２
＝２５＋１４４
＝１６９

（右辺）
＝ｃ^２
＝１３^２
＝１６９

（左辺）＝（右辺）になるから、５：１２：１３の関係が成り立つことが分かったね。

３辺の比５：１２：１３を使った問題

次の直角三角形の斜辺の長さｘを求めなさい。

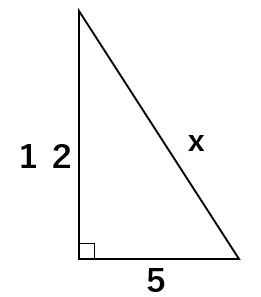
丁寧にやるのであれば、
三平方の定理ａ^２＋ｂ^２＝ｃ^２のａ、ｂに５、１２を代入して
５^２＋１２^２＝ｘ^２
２５＋１４４＝ｘ^２
ｘ^２＝１６９
ｘ＝±１３

と計算してもOK。

ただ直角三角形の３辺の比「５：１２：１３」を知っていたら、ｘ＝１３と一瞬で求めることができるんだよ。

次の円錐は底面の半径が５cm、母線の長さが１３cmのである。高さを求めなさい。

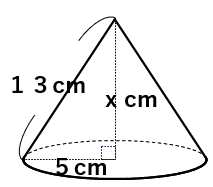
円錐から次のような直角三角形を抜き出して考えよう。

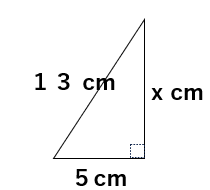
丁寧にやるのであれば、
三平方の定理ａ^２＋ｂ^２＝ｃ^２のａ、ｃに５、１３を代入して
５^２＋ｘ^２＝１３^２
２５＋ｘ^２＝１６９
ｘ^２＝１４４
ｘ＝±１２

と計算してもOK。

ただ直角三角形の３辺の比「５：１２：１３」だから、ｘ＝１２と一瞬で求めることができるんだよ。

三平方の定理を使って円錐の高さを求める問題はよく出るからしっかりマスターしておこう。
さらにレベルアップした問題だったら、円錐の体積まで求めるよ。

辺の比が８：１５：１７の直角三角形

また、数が大きくなってきたね。１５の２乗とか１７の２乗とかを計算するのは面倒だよね。
そんなとき５：１５：１７の関係を知っていれば、２乗の計算せずにできちゃう問題もあるよ。

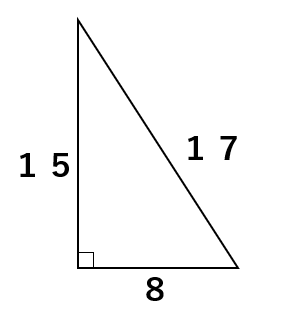
本当に８：１５：１７の関係が成り立つのか、三平方の定理ａ^２＋ｂ^２＝ｃ^２のａ、ｂ、ｃに数字を代入してみよう。

８、１５、１７のうち、最も長いものが斜辺ｃだから、ｃ＝１７になるよ。

（左辺）
＝ａ^２＋ｂ^２
＝８^２＋１５^２
＝６４＋２２５
＝２８９

（右辺）
＝ｃ^２
＝１７^２
＝２８９

（左辺）＝（右辺）になるから、８：１５：１７の関係が成り立つことが分かったね。

「８：１５：・・・。あれ？なんだったけ」ってなるかもしれない。そんなときは無理せず、三平方の定理を使って答えを求めることをおすすめするよ。

３辺の比８：１５：１７を使った問題

次の直角三角形のｘを求めなさい。

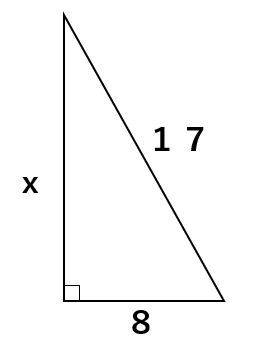
丁寧にやるのであれば、
三平方の定理ａ^２＋ｂ^２＝ｃ^２のａ、ｃに８、１７を代入して
８^２＋ｘ^２＝１７^２
６４＋ｘ^２＝２８９
ｘ^２＝２２５
ｘ＝±１５

と計算してもOK。

ただ直角三角形の３辺の比「８：１５：１７」を知っていたら、ｘ＝１５と一瞬で求めることができるんだよ。

辺の比が７：２４：２５の直角三角形

２４の２乗とか２５の２乗とかを計算するのは面倒だよね。
そんなとき７：２４：２５の関係を知っていれば、２乗の計算せずにできちゃう問題もあるよ。

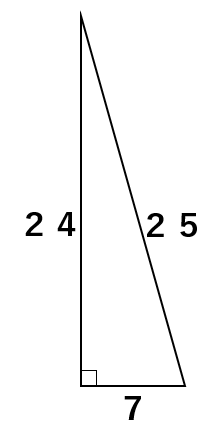
本当に７：２４：２５の関係が成り立つのか、三平方の定理ａ^２＋ｂ^２＝ｃ^２のａ、ｂ、ｃに数字を代入してみよう。

７、２４、２５のうち、最も長いものが斜辺ｃだから、ｃ＝２５になるよ。

（左辺）
＝ａ^２＋ｂ^２
＝７^２＋２４^２
＝４９＋５７６
＝６２５

（右辺）
＝ｃ^２
＝２５^２
＝６２５

（左辺）＝（右辺）になるから、７：２４：２５の関係が成り立つことが分かったね。

３辺の比７：２４：２５を使った問題

次の直角三角形のｘを求めなさい。

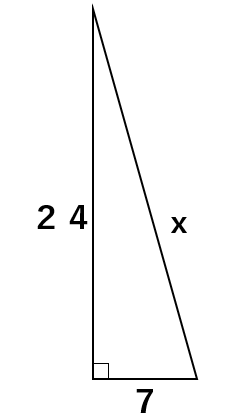
丁寧にやるのであれば、
三平方の定理ａ^２＋ｂ^２＝ｃ^２のａ、ｂに７、２４を代入して
７^２＋２４^２＝ｘ^２
４９＋５７６＝ｘ^２
ｘ^２＝６２５
ｘ＝±２５

と計算してもOK。

ただ直角三角形の３辺の比「７：２４：２５」を知っていたら、ｘ＝２５と一瞬で求めることができるんだよ。

２乗の計算がないから、間違えることもなくなるし、速く答えを求めることができるね。

覚えるべき３辺の比が整数の直角三角形のまとめ

３辺の比が整数の場合（ピタゴラス数）は全部で４つ説明してきたよ。
３辺の比を知っていると速く答えを求めることができることがわかったかな。

３辺の比と覚え方を下にまとめたよ。

３辺の比が整数の場合

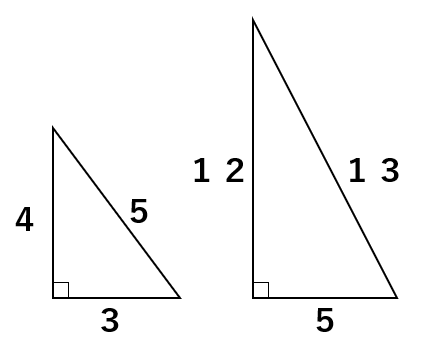
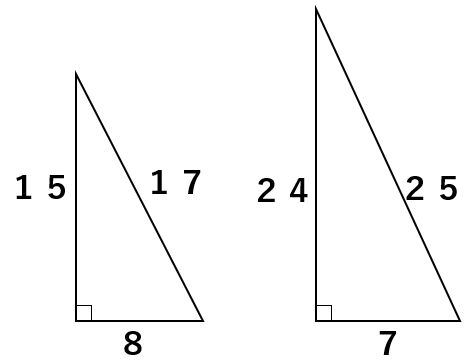
①３：４：５
「み（３）よ（４）こ（５）、」
②５：１２：１３
「こ（５）いつ（１２）は、とうさん（１３）のだ。」
③８：１５：１７
「はっ！（８）いちご（１５）いーな（１７）」
④７：２４：２５
「な（７）によ（２４）にこ（２５）あるじゃない」

こんな風に覚えよう

みよこちゃんと、お父さんがいて、ケーキを食べているんだ。
お父さんが、「こいつは父さんのだ」と言いつつ、みよこちゃんのケーキのイチゴに気がついて「はっ！イチゴいいな」と言ったんだけれど、お父さんのケーキにはイチゴが２個のっているので、みよこちゃんが「２個あるじゃない」とツッコミを入れているよ。

覚えるべき３辺の比にルートを含む直角三角形

今までは３辺の比が整数だったよね。今から紹介していく３辺の比にはルートが入ってくるよ。

３辺の比が１：２：\(\sqrt{５}\)の直角三角形

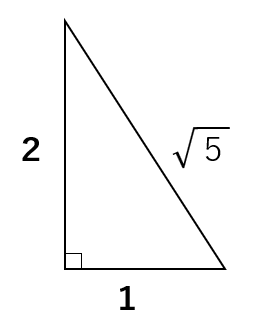
本当に１：２：\(\sqrt{５}\)の関係が成り立つのか、三平方の定理ａ^２＋ｂ^２＝ｃ^２のａ、ｂ、ｃに数字を代入してみよう。

１、２、\(\sqrt{５}\)のうち、最も長いものが斜辺ｃだから、ｃ＝\(\sqrt{５}\)になるよ。

（左辺）
＝ａ^２＋ｂ^２
＝１^２＋２^２
＝１＋４
＝５

（右辺）
＝ｃ^２
＝(\(\sqrt{５}\))^２
＝５

（左辺）＝（右辺）になるから、１：２：\(\sqrt{５}\)の関係が成り立つことが分かったね。

３辺の比１：２：\(\sqrt{５}\)を使った問題

次の直角三角形の斜辺の長さｘを求めなさい。

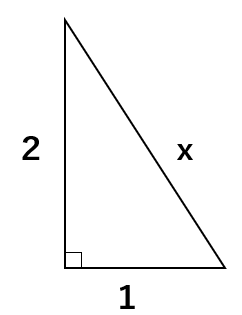
丁寧にやるのであれば、
三平方の定理ａ^２＋ｂ^２＝ｃ^２のａ、ｂに１、２を代入して
１^２＋２^２＝ｘ^２
１＋４＝ｘ^２
ｘ^２＝５
ｘ＝±\(\sqrt{５}\)

と計算してもOK。

ただ直角三角形の３辺の比「１：２：\(\sqrt{５}\)」を知っていたら、ｘ＝\(\sqrt{５}\)と一瞬で求めることができるんだよ。

次の直角三角形の斜辺の長さｘを求めなさい。

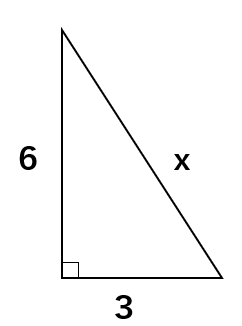
丁寧にやるのであれば、
三平方の定理ａ^２＋ｂ^２＝ｃ^２のａ、ｂに３、６を代入して
３^２＋６^２＝ｘ^２
９＋３６＝ｘ^２
ｘ^２＝４５
ｘ＝±\(\sqrt{４５}\)
ｘ＝±３\(\sqrt{５}\)

と計算してもOK。

ただ直角三角形の３辺の比「１：２：\(\sqrt{５}\)」だから、３つの辺の比を３倍すると「３：６：３\(\sqrt{５}\)」になるよね。

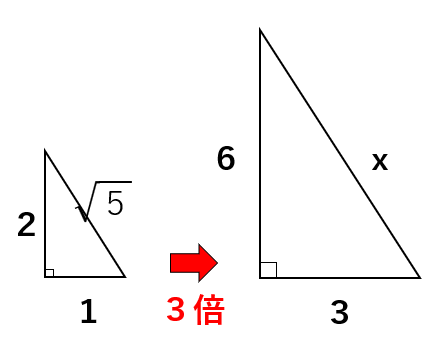
そうすると、ｘ＝３\(\sqrt{５}\)と一瞬で求めることができるんだよ。

３辺の比が１：１：\(\sqrt{２}\)の直角三角形

１：１：\(\sqrt{２}\)になるのは、次のような４５°、４５°、９０°の直角三角形限定だよ。

４５°、４５°、９０°の直角三角形がでてきたら「よっしゃー」と喜ぼう！

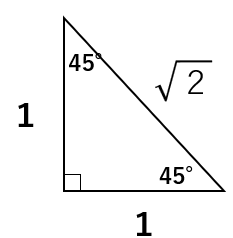
本当に１：１：\(\sqrt{２}\)の関係が成り立つのか、三平方の定理ａ^２＋ｂ^２＝ｃ^２のａ、ｂ、ｃに数字を代入してみよう。

１、１、\(\sqrt{２}\)のうち、最も長いものが斜辺ｃだから、ｃ＝\(\sqrt{２}\)になるよ。

（左辺）
＝ａ^２＋ｂ^２
＝１^２＋１^２
＝１＋１
＝２

（右辺）
＝ｃ^２
＝(\(\sqrt{２}\))^２
＝２

（左辺）＝（右辺）になるから、１：１：\(\sqrt{２}\)の関係が成り立つことが分かったね。

３辺の比１：１：\(\sqrt{２}\)を使った問題

次の直角三角形の斜辺の長さｘを求めなさい。

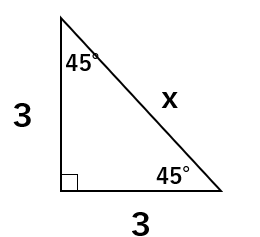
丁寧にやるのであれば、
三平方の定理ａ^２＋ｂ^２＝ｃ^２のａ、ｂに３、３を代入して
３^２＋３^２＝ｘ^２
９＋９＝ｘ^２
ｘ^２＝１８
ｘ＝±\(\sqrt{１８}\)
ｘ＝±３\(\sqrt{２}\)

と計算してもOK。

ただ直角三角形の３辺の比「１：１：\(\sqrt{２}\)」を３倍して「３：３：３\(\sqrt{２}\)」になるよね。

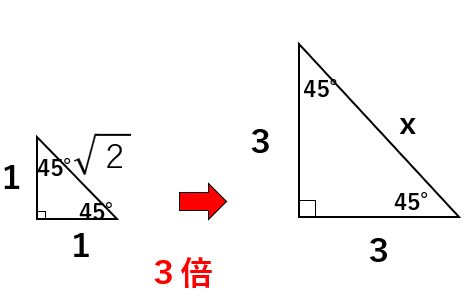
だから、ｘ＝３\(\sqrt{２}\)と一瞬で求めることができるんだよ。

３辺の比が１：\(\sqrt{３}\)：２の直角三角形

１：\(\sqrt{３}\)：２になるのは、次のような３０°、６０°、９０°の直角三角形限定だよ。

３０°、６０°、９０°の直角三角形がでてきたら「よっしゃー」と喜ぼう！

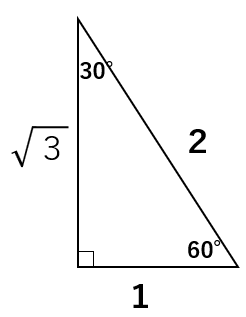
本当に１：\(\sqrt{３}\)：２の関係が成り立つのか、三平方の定理ａ^２＋ｂ^２＝ｃ^２のａ、ｂ、ｃに数字を代入してみよう。

１：\(\sqrt{３}\)：２のうち、最も長いものが斜辺ｃだから、ｃ＝２になるよ。

（左辺）
＝ａ^２＋ｂ^２
＝１^２＋(\(\sqrt{３}\))^２
＝１＋３
＝４

（右辺）
＝ｃ^２
＝２^２
＝４

（左辺）＝（右辺）になるから、１：\(\sqrt{３}\)：２の関係が成り立つことが分かったね。

１：\(\sqrt{３}\)：２の覚え方

３０°、６０°、９０°の直角三角形を次のように組み合わせると正三角形になるよね。

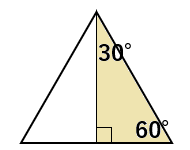
直角三角形の底辺が１だと、正三角形の１辺は２になるから、１：２。

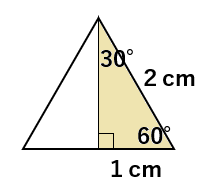
直角三角形に注目して、高さをｘとすると、
１の２乗＋ｘの２乗＝２の２乗になって
ｘ＝\(\sqrt{３}\)
になるよ。

ちなみに、１：\(\sqrt{３}\)：２は、ゴロがいいということで、「１：２：\(\sqrt{３}\)」と覚える場合もあるかもしれない。
もちろんそれでもいいんだけれど、斜辺は「２」であって、「\(\sqrt{３}\)」ではないことに注意しよう。

もし、「どっちが斜辺だっけ？」と自信がなくなってしまったら、\(\sqrt{３}\)の近似値が「1.7320508」であることを思い出そう！
そうすれば、\(\sqrt{３}\)と２を比べたときに、２の方が大きいので、「一番大きいから、２が斜辺だ！」と思い出すことができるよ。

３辺の比１：\(\sqrt{３}\)：２を使った問題

次の直角三角形の高さを求めなさい。

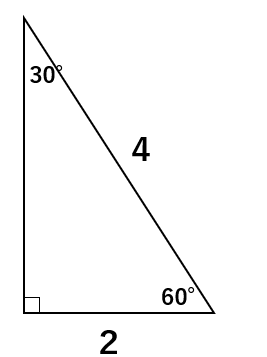
丁寧にやるのであれば、高さをｘとして
三平方の定理ａ^２＋ｂ^２＝ｃ^２のａ、ｃに２、４を代入して
２^２＋ｘ^２＝４^２
４＋ｘ^２＝１６
ｘ^２＝１２
ｘ＝±\(\sqrt{１２}\)
ｘ＝±２\(\sqrt{３}\)

と計算してもOK。

ただ直角三角形の３辺の比「１：\(\sqrt{３}\)：２」を２倍して「２：２\(\sqrt{３}\)：４」になるよね。

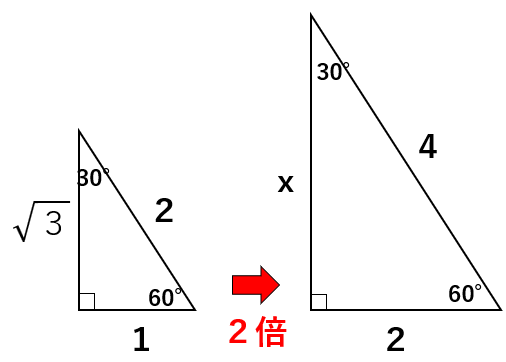
だから、ｘ＝２\(\sqrt{３}\)と一瞬で求めることができるんだよ。

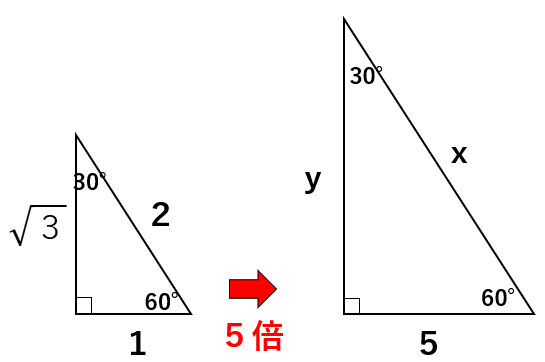
次の直角三角形でｘの長さを求めなさい。

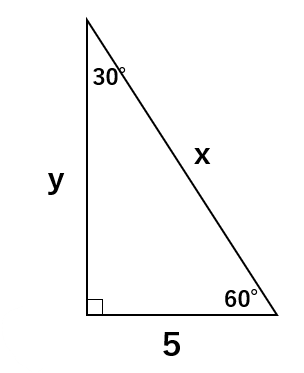
３０°、６０°、９０°の特別な直角三角形の３辺の比は１：\(\sqrt{３}\)：２になるんだよね。今回、底辺が５倍になっているから全部５倍するとｘ＝１０、ｙ＝５\(\sqrt{３}\)と求めることができるよ。

覚えるべき３辺の比にルートを含む直角三角形のまとめ

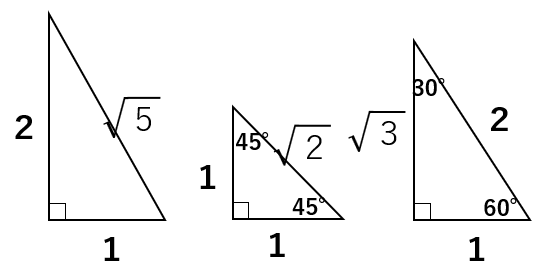
⑤１：２：\(\sqrt{５}\)
⑥１：１：\(\sqrt{２}\)
⑦１：\(\sqrt{３}\)：２

「〇：〇：斜辺」→最後の数字が斜辺になるからね。　

「三平方の定理」覚えるべき３辺の比７つのパターンまとめ

「三平方の定理」覚えるべき３辺の比７パターン
を知っていると、２乗の計算することなく答えを求めることができるんだったよね。

「覚えるべき３辺の比」は覚えていなくてもなんとか計算で求められるけど、知っていると速く答えが求められるよ。

中学生で覚えておいてほしい、三平方の定理の比の７パターンは次の通り

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。