「連立方程式の解」をグラフの交点で求める方法をわかりやすく解説
中学2年生の数学で学習する、連立方程式の解を、2つの二元一次方程式のグラフの交点から求める方法をわかりやすく解説するよ。
2つの二元一次方程式のグラフの交点を調べてみよう
「二元一次方程式のグラフの書き方」で説明したように、二元一次方程式はグラフで書くことができたね。
今回は、2つの二元一次方程式のグラフの交わる点(交点)について確認していくよ。
例題
次の2つの二元一次方程式のグラフを書いて、交点の座標を求めなさい。
2χ+y=1
χ-y=-4
まずは、それぞれの式を「y=」の形に変形して、傾きと切片を求めるところからスタートしよう。
2χ+y=1
↓2χを右辺に移項
y=-2χ+1 傾き-2、切片1
χ-y=-4
↓χを右辺に移項
-y=-χ-4
↓両辺に-1を掛ける
y=χ+4 傾き1、切片4
傾きと切片がわかったから、2つのグラフを書こう。
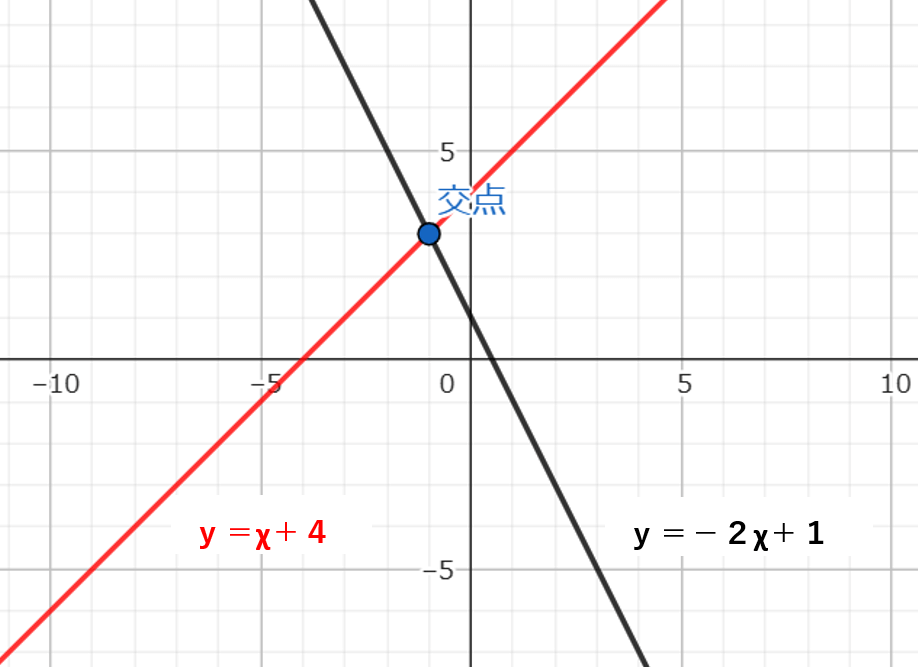
グラフを見ると交点の座標は、(-1、3)ということがわかるね!
連立方程式の解をもとめてみよう
次に上の例題の2つの式を組み合わせた連立方程式の解を求めてみよう。
例題
連立方程式\begin{cases}2χ+y=1\\χ-y=-4\end{cases}の解を求めなさい。
※連立方程式の解き方が不安な人は、「連立方程式(二元一次方程式)の解き方「加減法・代入法」を解説」で確認しよう。
今回は2つの式のたし算すると、計算することができるね。
2χ+y= 1
+) χーy=-4
3χ =-3
χ =-1
χ=-1を2χ+y=1に代入してyを求めよう。
2×(-1)+y=1
-2 +y=1
y=3
この連立方程式の解は、χ=-1、y=3ということがわかったね。
連立方程式の解とグラフの交点
2つの二元一次方程式のグラフの交点の座標と連立方程式の解を見てみると、「グラフの交点の座標=連立方程式の解」という関係になっていることに気がついたかな?
この考え方は、これから出てくる問題でもよく使うから覚えておこう!
ここからは、「グラフの交点の座標=連立方程式の解」の考え方を使った問題にチャレンジしていくよ。
例題
次の2つの直線の式と交点の座標を求めなさい。
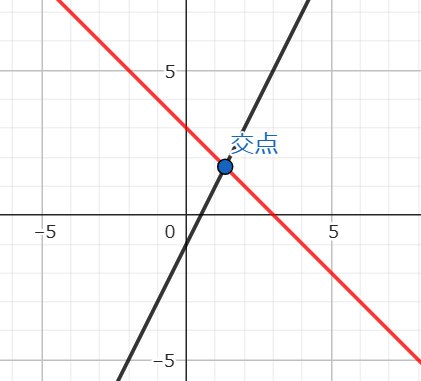
グラフを見てみると、交点が読み取りやすい値ではないことがわかるね。
このパターンの時には、
(1)2つの直線の式を求める
(2)2つのグラフの式を使って、連立方程式の解を求める
という手順で求めるよ。
(1)2つの直線の式を求める
まずは、グラフから直線の式を求めよう。
グラフから直線の式を求める時の手順について復習しよう。
グラフから直線の式を求める手順
①グラフから切片を求める
②χのプラス側で読み取りやすい点を見つける
③切片から②の点まで「右にいくつ進んだか」「上下にいくつ進んだか」を求める
④③で求めた値をa=\(\frac{上下に進んだ数}{右に進んだ数}\)に代入してaを求める
※忘れてしまった人は、「一次関数の式の求め方をパターン別にわかりやすく解説」で確認しよう。
右上がりの黒い直線の式を使って、一次関数の式の求め方を復習するよ。
右下がりの赤い直線の式は、自分の力で求めてみよう!
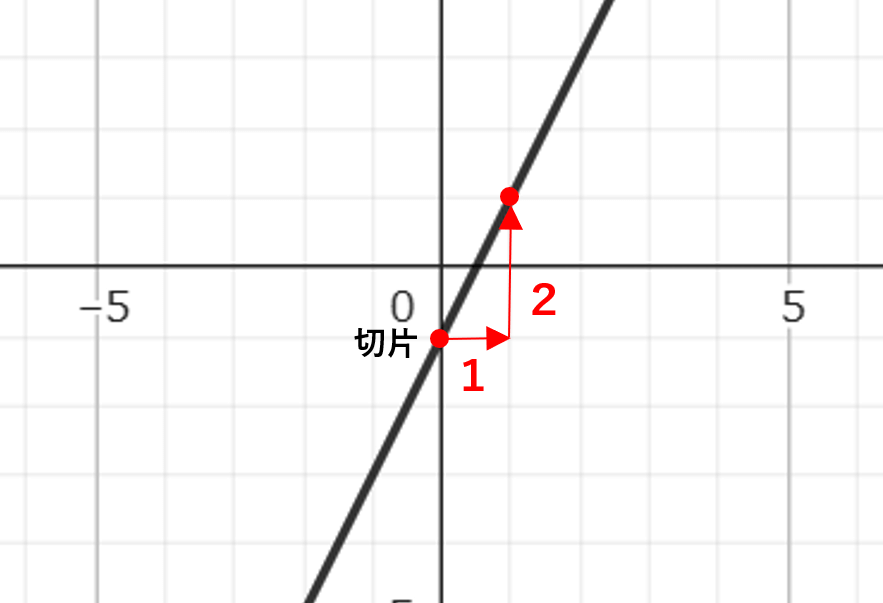
①グラフから切片を求める
グラフを見ると、切片の座標は(0、-1)だから、y=aχ+bのb(切片)は-1ということがわかるね!
②χのプラス側で読み取りやすい点を見つける
上のグラフの切片ではない方の赤い点(1、1)が読み取りやすい点だよ。
③切片から②の点まで「右にいくつ進んだか」「上下にいくつ進んだか」を求める
切片から②で求めた点までは、グラフを見てわかる通り「右に1」「上に2」進んだ点ということがわかるね。
④③で求めた値をa=\(\frac{上下に進んだ数}{右に進んだ数}\)に代入してaを求める
aを求める式に代入すると
a=\(\frac{2}{1}\)
=2
と求めることができるよ。
①から④で求めた値から、右上がりの黒い直線の式はy=2χ-1と求めることができたね。
同じように右下がりの赤い直線の式を求めると、y=-χ+3になるよ。
(2)2つのグラフの式を使って、連立方程式の解を求める
(1)で求めた2つの式を連立方程式として解を求めよう。
\begin{cases}y=2χ-1\\y=-χ+3\end{cases}
どちらも「y=」の形だから、代入法を使って計算すると簡単に求めることができるね!
※代入法が苦手な人は加減法で解くのもOKだけど、計算ミスをしないように注意しよう。
y=2χ-1のyに、y=-χ+3の-χ+3を代入すると、-χ+3=2χ-1となるよ。
あとは計算を進めてχを求めていこう。
-χ+3=2χ-1
↓2χを左辺へ、+3を右辺へ移項
-χ-2χ=-1-3
↓
-3χ=-4
↓両辺に-\(\frac{1}{3}\)をかけて、「χ=」の形に変形
-\(\frac{1}{3}\)×-3χ=-\(\frac{1}{3}\)×-4
χ=\(\frac{4}{3}\)
χ=\(\frac{4}{3}\)をy=2χ-1に代入してyを求めよう。
y=2×\(\frac{4}{3}\)-1
↓右辺は、通分して(分母を3に揃えて)計算をする
y=\(\frac{8}{3}\)-\(\frac{1}{1}\)
=\(\frac{8}{3}\)-\(\frac{1×3}{1×3}\)
=\(\frac{8}{3}\)-\(\frac{3}{3}\)
=\(\frac{5}{3}\)
計算結果から、2つの直線の式の交点は(\(\frac{4}{3}\)、\(\frac{5}{3}\))と求めることができたね。
今回の例題のように、交点の値が読み取りにくいパターンもテストでは出題されるから、求める手順を忘れないように復習しよう。
応用問題にチャレンジ!
2つの直線の交点の座標を求めなさい。
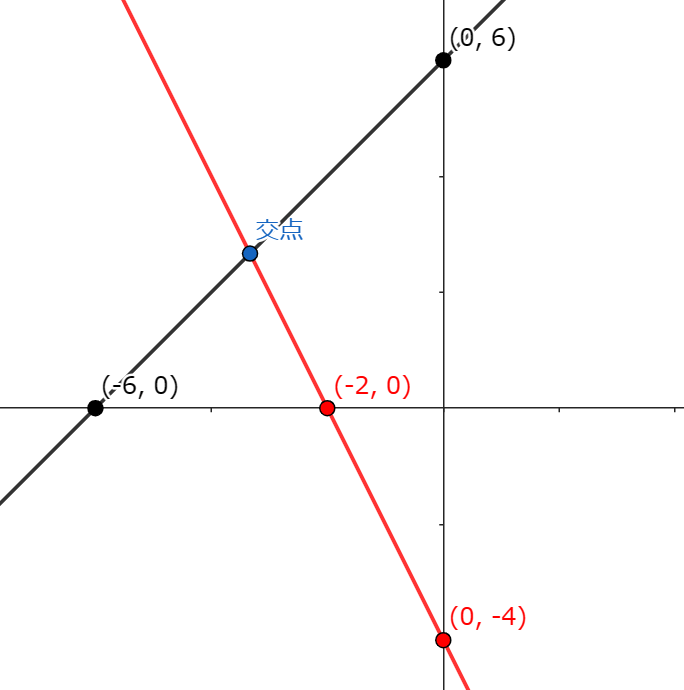
この問題も解く手順は、
(1)2つの直線の式を求める
(2)2つのグラフの式を使って、連立方程式の解を求める
で進めていこう。
(1)2つの直線の式を求める
今回の問題では、切片がわかっているけれど、切片の右側の点がわからないから、直線の求め方で困った人も多かったかな?
2点がわかっている時の傾きを求める方法を使うと、簡単に求めることができるよ。
左側にある点から、右側にある点に「右にいくつ進んだか」「上下にいくつ進んだか」を求めて、a=\(\frac{上下に進んだ数}{右に進んだ数}\)に代入すると傾きを求めることができるよ。
右上がりの黒い直線を使って解き方を確認していこう。
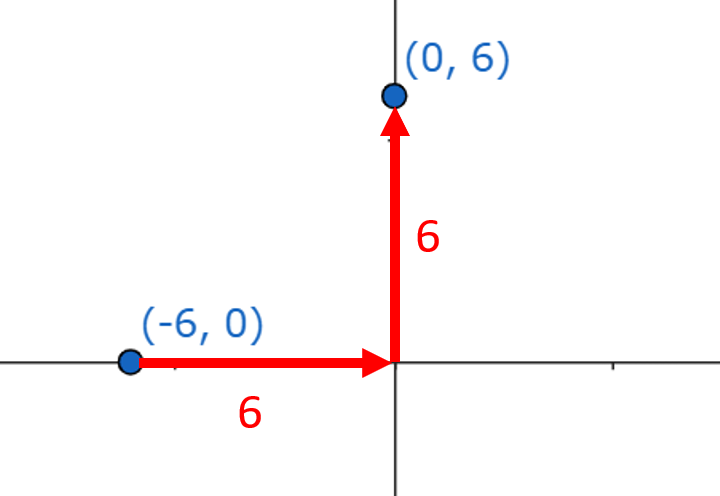
図を見てわかる通り、左側の点(-6、0)から右側の点(0、6)に向けて「右に6」「上に6」進んでいるね。
だからこの直線の傾きは、a=\(\frac{上下に進んだ数}{右に進んだ数}\)に代入したら、a=1と求めることができるよ。
bは座標からb=6ということがわかるね。
これで右上がりの黒い直線は、y=χ+6と求めることができるよ。
右下がりの赤い直線も同じように解き進めていこう。
左側の点(-2、0)から右側の点(0、-4)に向けて「右に2」「下に4」進んでいるからa=-2
bは座標からb=-4となるので、
右下がりの直線は、y=-2χ-4と求めることができるよ。
(2)2つのグラフの式を使って、連立方程式の解を求める
ここからは、例題と同じように(1)で求めた2つの式を連立方程式で計算していこう。
\begin{cases}y=χ+6\\y=-2χ-4\end{cases}
y=χ+6のyに、y=-2χ-4の-2χ-4を代入すると、-2χ-4=χ+6となるよ。
あとは計算を進めてχを求めると、χ=-\(\frac{10}{3}\)
次にχ=-\(\frac{10}{3}\)をy=χ+6に代入してyを求めると、y=\(\frac{8}{3}\)
計算結果から、2つの直線の式の交点は(-\(\frac{10}{3}\)、\(\frac{8}{3}\))と求めることができるよ。
「グラフの交点の座標=連立方程式の解」の関係については、一次関数の応用問題でも良く出るパターンだから、教科書や学校のワークの問題を解いて復習しよう!
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


