証明とは?平行線の性質を使って三角形の角の性質を証明してみよう
中学2年生の数学で学習する「証明」について、証明とはどういうことか?
証明する方法や考え方を学ぶために、平行線の性質を使って三角形の角の性質(内角の和が180度であること、三角形の外角は、それととなり合わない2つの内角の和に等しいこと)を証明する方法をくわしく解説するよ。
「証明」とは
新しい単元として「証明」がスタートするよ。
証明って言葉を聞くとなんだか難しそうな感じがするよね。
まずは証明の言葉の意味から確認しよう。
証明とは、本当かどうかわからないことを、事実(すでに正しいとわかっていること)をつかって説明すること
算数・数学で出てきた円の面積の公式(半径×半径×π)を覚えているかな?
「公式だから覚えるのが当たり前」と思っている人がいるかもしれないけれど、実際にはこの公式も正しいことが証明されたから使うことができるんだ。
円の面積の公式について
さっきの証明の言葉の意味から、
本当かどうかわからないこと(円の面積の公式がπr2)
すでに正しいとわかっていること(長方形の面積の求め方が「たて×横」)
として説明するね。
①半径がrの円を64等分するよ。
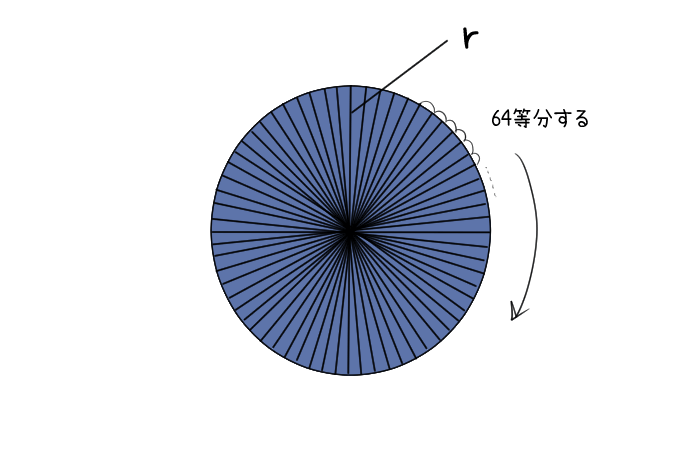
②64等分したおうぎ形を交互に並べるとたての長さが円の半径r、横の長さが円周の半分のπrの長方形に近い形になるよ。
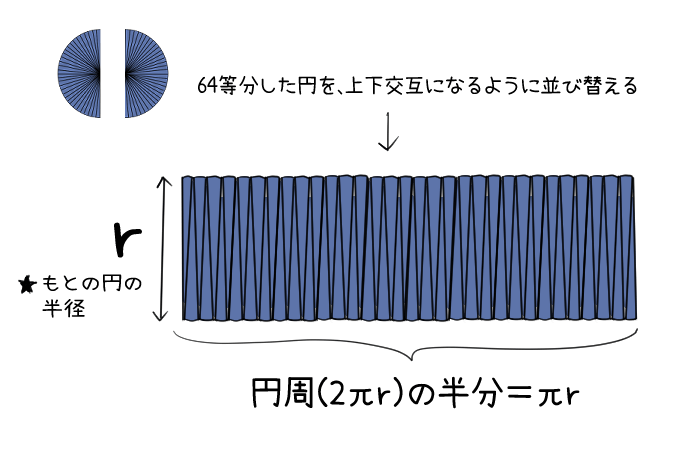
長方形の面積の「たて×横」に、上のおうぎ形を交互に並べた図の「たてをr、横をπr」として代入すると、r×πr=πr2となって円の面積の公式を導くことができるんだ。
※厳密には、高校生で習う数学の知識を使って証明するよ。
正しいと思えることでも、証明して説明できなければ間違っている可能性があるんだ。
実際にこれまで習った三角形の内角の性質について、正しいといえるか証明してみよう。
三角形の内角の性質を証明してみよう
三角形の内角の和は180°になる、ということは小学校から習ってきた当たり前のことだけれども、本当に正しいと言えるか次の例題を使って確認しよう。
例題
下の図のように、△ABCの頂点Cを通り、辺ABに平行な直線CEをひきます。
この図を利用して、三角形の内角の和が180°であることを証明しなさい。
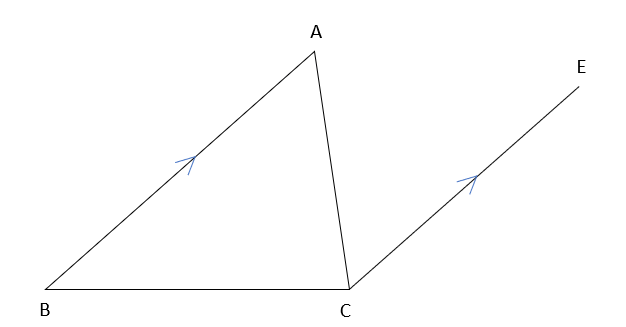
まずは、同じ角の大きさを見つけるところからスタートしよう。
また、辺BCを延長したところに点Dを作って証明を進めていくよ。
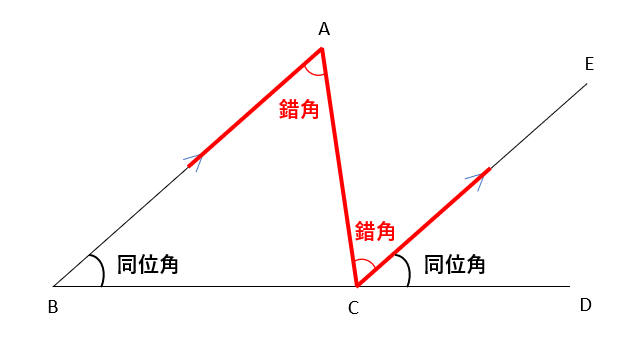
AB∥ECより、平行線の錯角(アルファベットのZと逆Zの形をしたところにできる角)は等しいから
∠BAC=∠ECA・・・①
AB∥ECより、平行線の同位角は等しいから
∠ABC=∠ECD・・・②
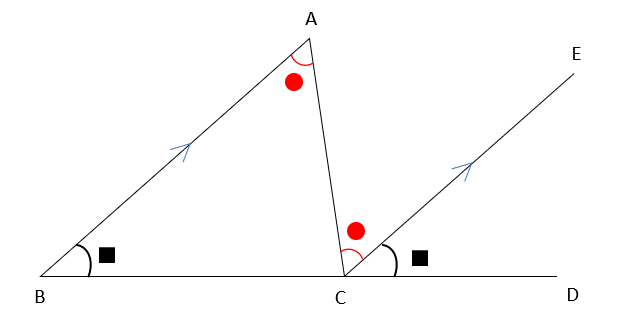
一直線が作る角の大きさは180°だから
∠ACB+∠ECA+∠ECD=180°
①と②から
赤い●がついた2つの角(∠BACと∠ECA)
黒い■がついた2つの角(∠ABCと∠ECD)
は、それぞれ大きさが等しいので、∠BAC+∠ABC+∠ACB=180°となるから、三角形の内角の和は180°になることが証明できるんだ。
三角形の外角の性質を証明してみよう
三角形の外角の性質について確認しよう。
※外角について忘れてしまった人は、「多角形の内角の和と外角の和の求め方をわかりやすく解説」で確認しよう。
上の三角形の内角の和の証明から、
三角形の外角は、それととなり合わない2つの内角の和に等しい、という性質を導くことができるんだ。

証明で使った上の図から、∠BAC+∠ABC=∠ECA+∠ECDとなるよね。
つまり、
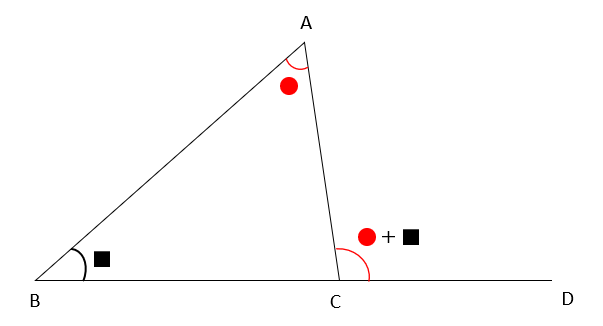
∠ACD=∠BAC+ABCとなるんだ。
この三角形の外角の性質は、角度計算の問題でもよく使う性質だから問題演習をしてマスターしよう。
問題
下の図で、∠χの大きさを求めなさい。
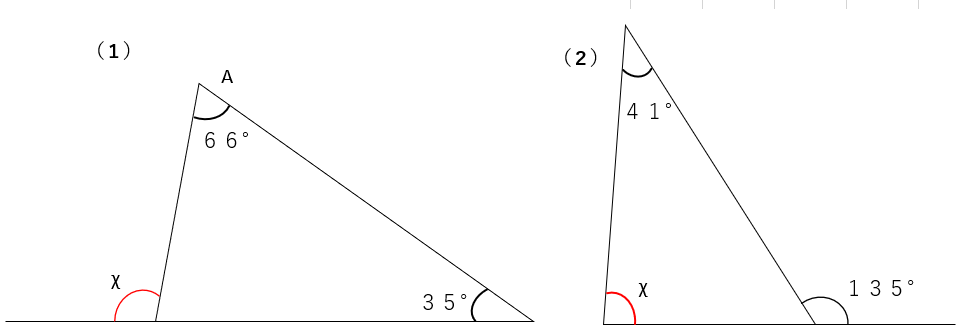
(1)
三角形の外角の性質を使うと、∠66°+∠35°=∠χという式を作ることができるから、あとは計算を進めていこう。
∠χ=101°
(2)
(1)と同じように、三角形の外角の性質を使うと、∠41°+∠χ=135°という式を作ることができるね。
∠χ=94°
別な解き方として、三角形の内角の和が180°という性質を使った方法を(2)を使って説明するね。
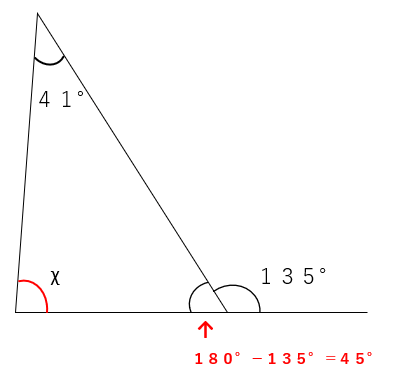
135°ととなり合う角度の大きさは、180°ー135°=45°
三角形の内角の和は、180°だから、∠χ+∠41°+∠45°=180°
これを計算すると、∠χ=94°と求めることができるよ。
三角形の外角の性質を使う解き方に比べて、計算量が多くなってしまうので、計算ミスをする可能性が高くなるから注意しよう。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


