いろいろな確率「起こらない確率の求め方」公式を解説（練習問題）

中学２年生の数学で学習する、いろいろな確率について、「起こらない確率」の求め方をわかりやすく解説するよ。

「起こらない確率」とはどんな確率のことなのか、起こらない確率を求めるための公式、起こらない確率を求める練習問題を紹介しているよ。

いろいろな確率「起こらない確率の求め方」 公式を解説（練習問題）のPDF（4枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 「起こらない確率」の求め方
• 「起こらない確率」公式
• 「起こらない確率」の問題
• まとめ

「起こらない確率」の求め方

これまでは、「さいころを振って２が出る確率」や「５人から２人を選ぶ確率」のように、「起こる確率」について求めてきたよね。

今回は、「起こる確率」と反対の「起こらない確率」について勉強するよ！
※「起こらない確率」も別な表現として、「出ない確率」「ならない確率」「選ばれない確率」、くじの問題では、「外れる確率」などがあるよ。

早速、例題を使って「起こらない確率」の求め方を確認しよう。

さいころを１つ振った時に出るのは、「１・２・３・４・５・６」の６通りだよね。
その中で、４が出ないということは、「１・２・３・５・６」の目が出る５通りだから、その時の確率は\(\frac{５}{６}\)になるよ。

今回はさいころを１つ振った時だから、「４が出ない確率」はすぐに求めることができたけれど、
「さいころを２つ振った時に、出た目の和が５にならない確率」のように複雑になると求めるのは難しそうだよね。

そこで、次は「起こらない確率」を簡単に求めることができる公式について説明するよ。

「起こらない確率」公式

上の例題の「４が出ない確率」は\(\frac{５}{６}\)だったね。
この時、「４が出る確率」を見てみると、\(\frac{１}{６}\)ということがわかるね。

ここで、「４が出る確率」と「４が出ない確率」を足すと１になることに気がついたかな？

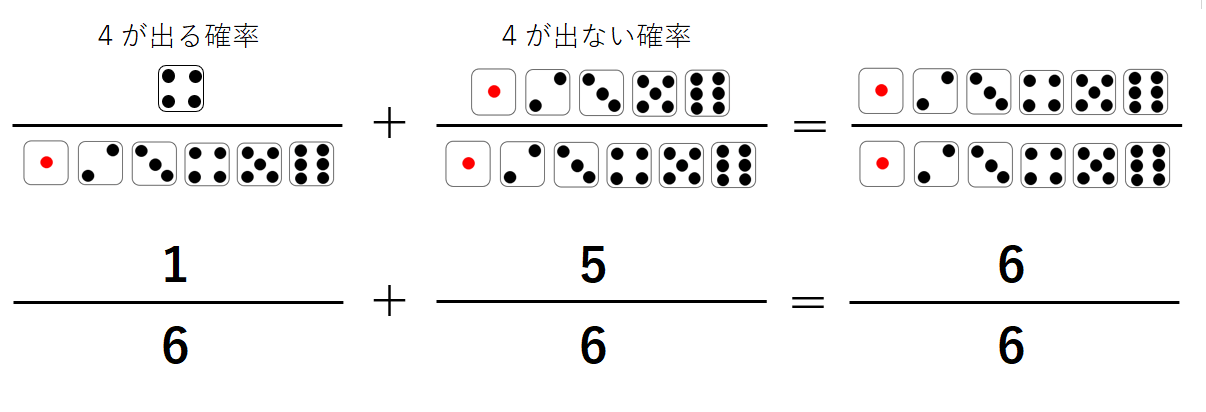
確率は、この問題のように１つの出来事について「起こる確率」と「起こらない確率」を足すと１になるんだ。

この考え方を利用すると、下の公式を導くことができるよ。

確率の問題では、「起こる確率」の方が簡単に見つけることが多いから、この公式を使うことで時間短縮ができて、数え間違いのミスを減らすことができるよ。

「起こらない確率」の問題

上で説明した「起こらない確率」の公式を使って問題にチャレンジしよう！

まずは、さいころを２個振った時の起こりうる場合を全て書きだそう。

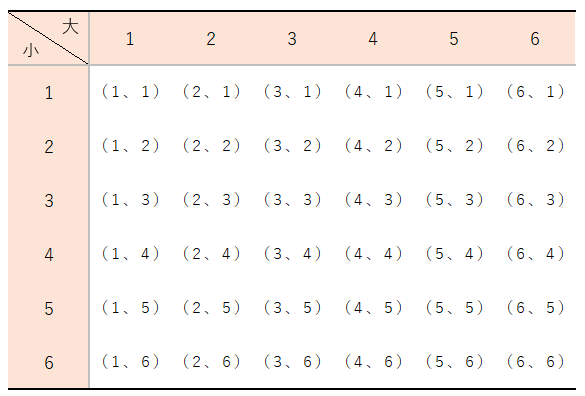
この中から５にならない場合を求めると数が多くて大変そうだよね。
そこで起こらない確率の公式を使って求めていこう。

今回は、出た目の和が５にならない時だから、「出た目の和が５になる時」の確率を求めるところからスタートしよう。

出た目の和が５になるのは、（１、４）（２、３）（３，２）（４、１）の時だから、その時の確率は

\(\frac{４}{３６}\)＝\(\frac{１}{９}\)

と求めることができるね。

これを使って、「出た目の和が５にならない時」の確率を求めると

１ー\(\frac{１}{９}\)＝\(\frac{８}{９}\)

と求めることができるよ。

実際に、「出た目の和が５にならない時」を数えると３２通りあるから、公式を使わないと大変だよね。

確率の問題で一番多い間違いが、数え間違いによるミスだから、ミスを減らすためにも、公式を使ってミスなく正確に、そして効率的に問題を解いていこう。

「起こらない確率の求め方」まとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。