平行線と面積の関係とは？性質と問題の解き方をわかりやすく解説

中学校２年生の数学で学習する「平行線と面積」について、平行線と面積の関係・性質をわかりやすく解説するよ。

平行線と面積の関係を使った問題の紹介と、解き方をくわしく解説していくよ。

平行線と面積の関係とは？性質と問題の解き方をわかりやすく解説のPDF（8枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

平行線と面積の関係

平行線と面積にはどんな関係があるのかな？

今回は面積が主役のお話なんだけれど、まずは小学生の時の復習として、これから紹介する３つの三角形の面積を求めてみよう。

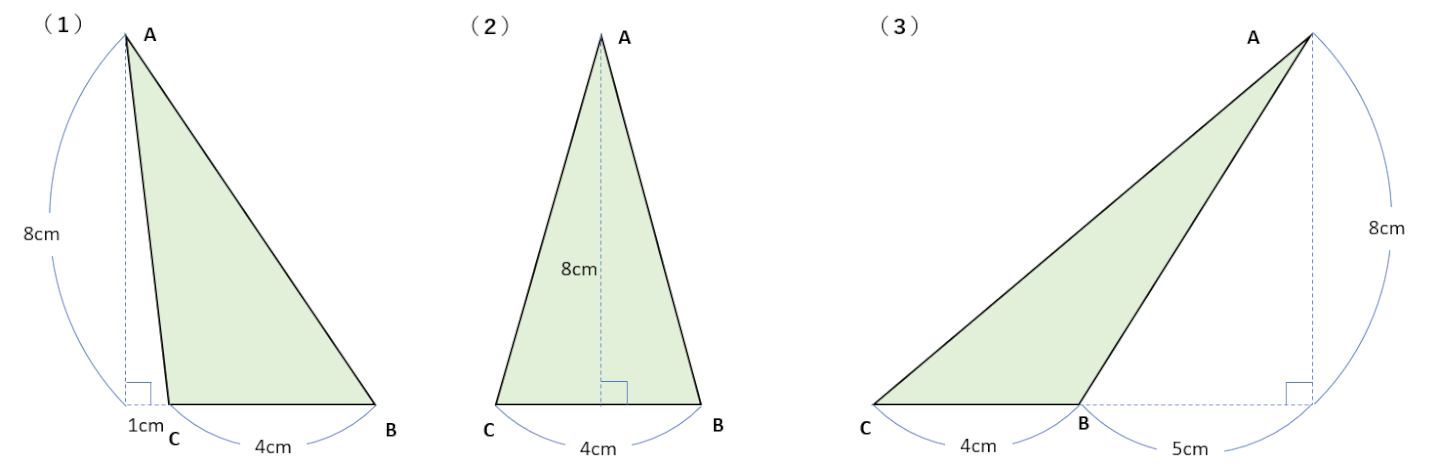
三角形の面積の求め方は、「底辺×高さ×\(\frac{１}{２}\)」だったね。
この公式を使って（１）から求めていこう。

（１）
この図形では底辺は４ｃｍ、高さは８ｃｍになるから公式に代入すると１６ｃｍ^２と求めることができるね。
底辺の長さを１ｃｍや５ｃｍと間違えてしまう人もいるから注意しよう！

（２）
この問題は特に引っ掛けはなく、底辺は４ｃｍ、高さは８ｃｍだから公式に代入すると１６ｃｍ^２と求めることができるね。

（３）
この問題も（１）と同じように底辺の長さを５ｃｍや９ｃｍと考えて間違えてしまう人がいるけれども、底辺は４ｃｍ、高さは８ｃｍになるから公式に代入すると１６ｃｍ^２と求めることができるね。

今回紹介した３つの三角形は形は違うけれど面積は全て１６ｃｍ^２となったね。
なぜなら、３つとも底辺の長さが同じ４ｃｍで、高さも同じ８ｃｍだからね。
三角形の面積の求め方は「底辺×高さ×\(\frac{１}{２}\)」なのだから、底辺と高さが同じ三角形はすべて同じ面積になるのはあたりまえだね。

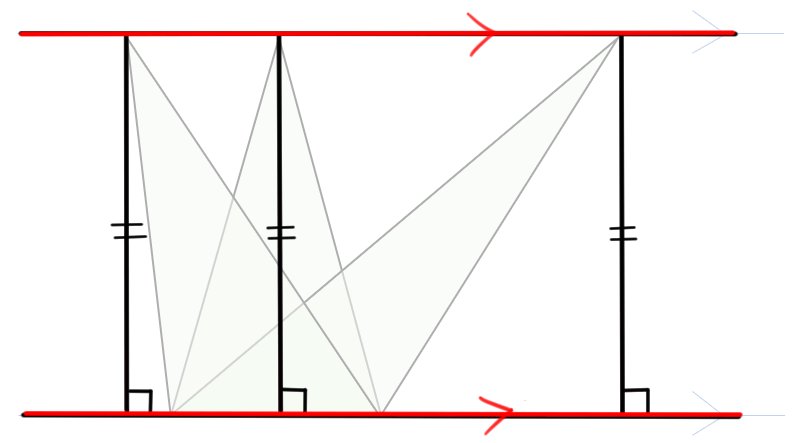
この３つの三角形の底辺を揃えて重ねてみると下の図のようになるよ。

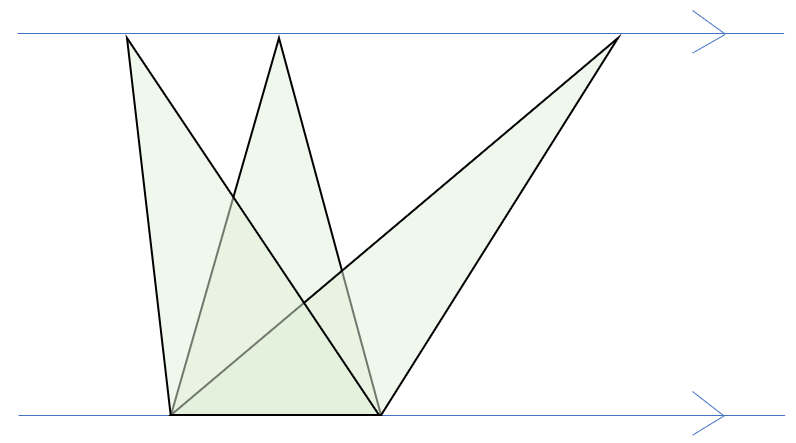
それぞれの三角形の頂点Aを結んだ線と、底辺が平行になっていることに気づいたかな？

上の図から、平行な２つの線分の中にできる底辺が等しい三角形の面積は、等しくなる、ということを覚えておこう！

どうして平行になるの？と思ったら読もう！

どうして平行になるのかというと、それぞれの三角形の底辺が同じで、底辺に対して直角である「高さ」がそれぞれ同じだからだね。

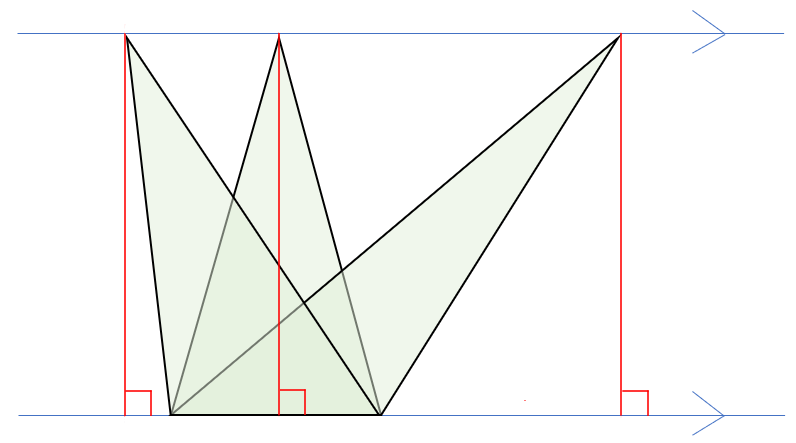
底辺を含む直線と、高さを表す直線、同じ高さの頂点部分を結んだ直線に注目してみよう。

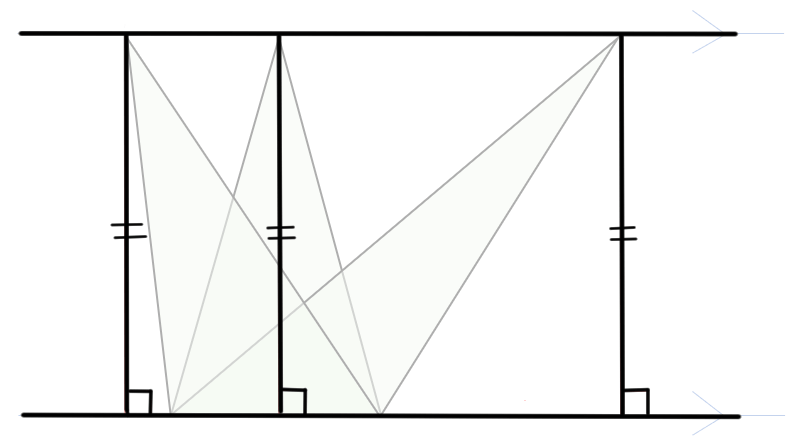
底辺を含む直線に対して垂直な高さを表す直線が同じ長さなので、その頂点部分を結んだ直線は、底辺を含む直線と平行になるというわけだね。

ではこの考え方を使って、次の問題にチャレンジしよう！

問題
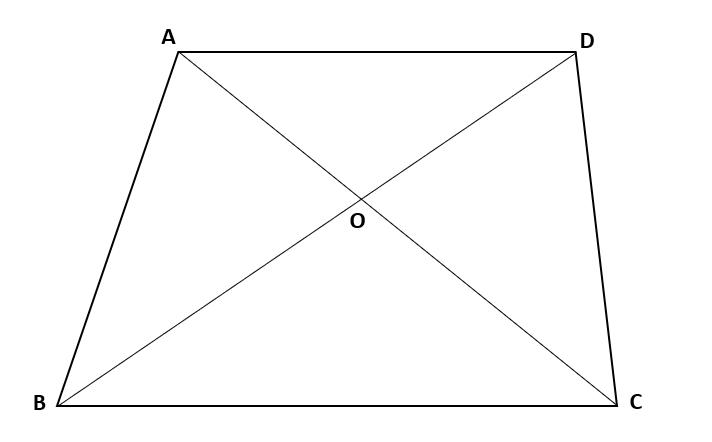
下の図は、AD∥BCである台形ABCDで、対角線ACとBDの交点をOとする時、次の（１）から（３）の三角形と面積が等しい三角形を答えなさい。
（１）△ABC
（２）△ADB
（３）△ABO

（１）
△ABCの底辺をBCとして考えよう。
ADとBCの平行な２つの線分の中にできる底辺がBCの三角形は、△BCDだね。

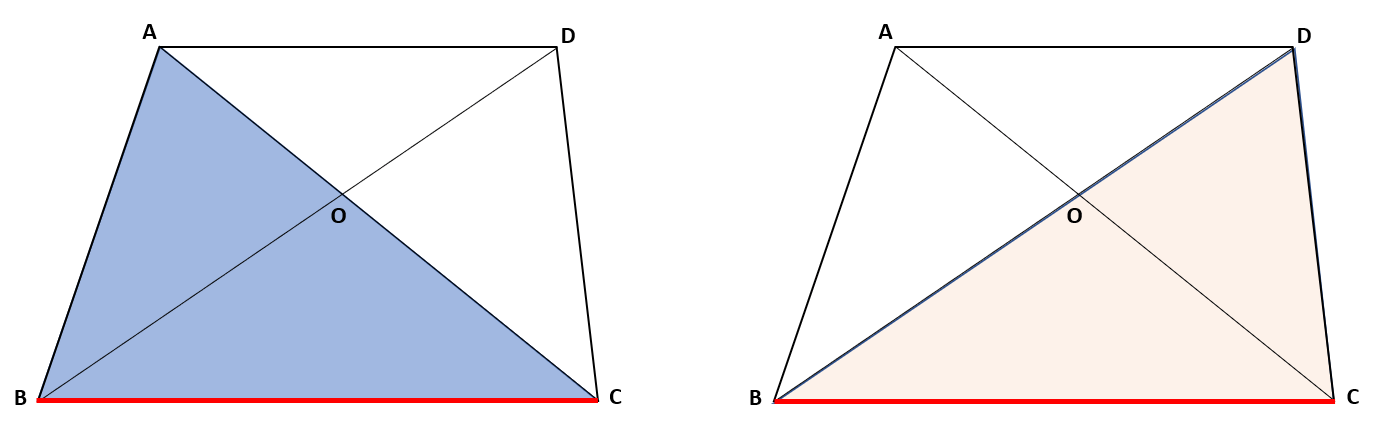
答え　△BCD

（２）
△ADBの底辺をADとして考えよう。
ADとBCの平行な２つの線分の中にできる底辺がADの三角形は、△ADCだね。

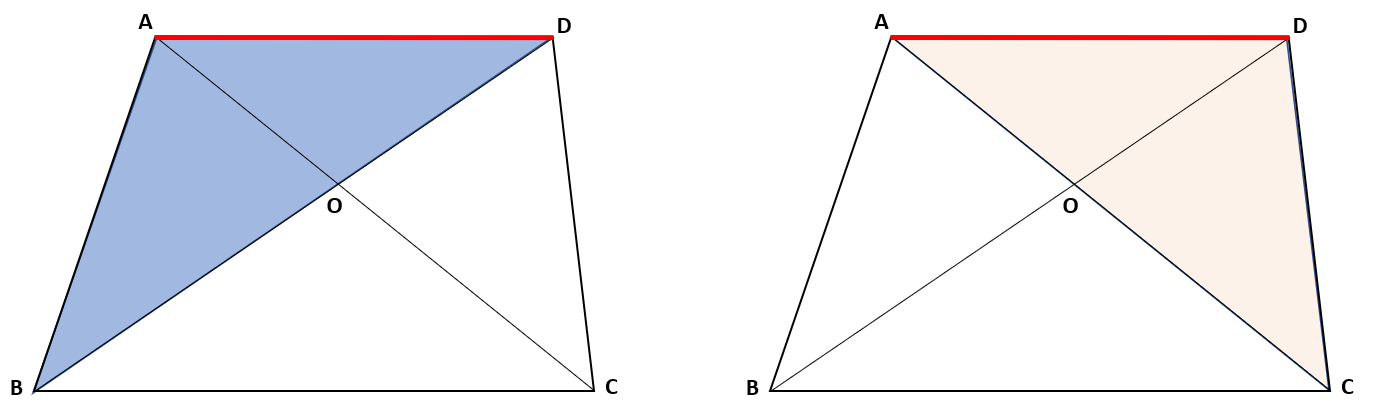
答え　△BCD

（３）
最後の問題は、答えとなる三角形を見つけることができなくて困った人も多かったかな？
（１）や（２）のように△ABOは平行な２つの線分にはさまれていないよね。
この問題は、同じ大きさの三角形の面積から２つの図形に共通している部分（重なっている部分）を引くと見つけることができるよ。

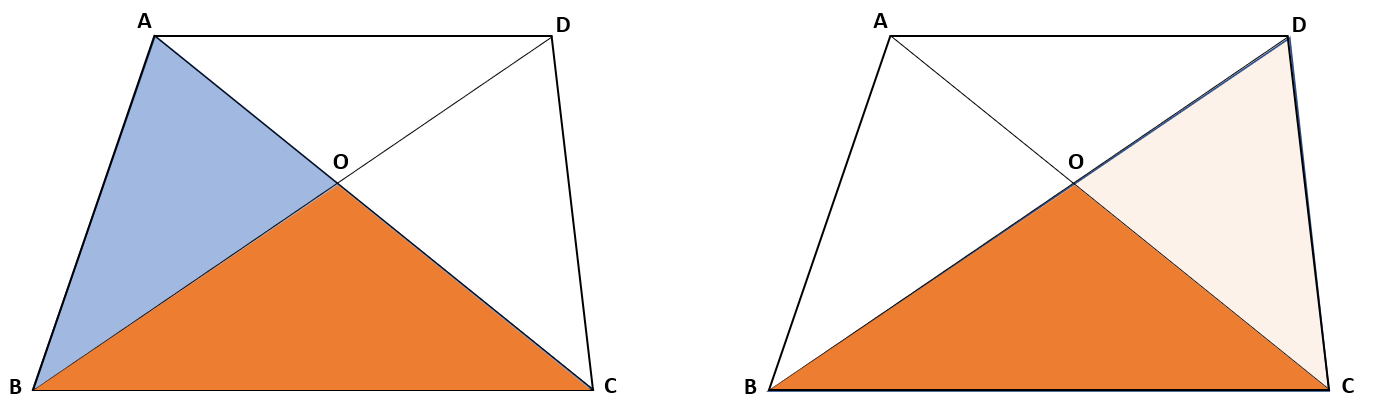
（１）で見つけた△ABCと△BCDに注目しよう。
そうすると２つの図形の共通している部分は△OBCだから、これを利用して考えよう。
△ABO＝△ABCー△OBC
△DOC＝△BCDー△OBC
だから、△ABOと面積が等しい三角形は、△DOCとなるよ。

答え　△DOC

この平行線と面積の関係を利用した問題は、図形の問題以外でも登場するからしっかりマスターしておこう！

四角形の面積を変えずに三角形にしてみよう

次は、平行線と面積の関係を利用して作図の問題にチャレンジしよう。

例題
下の図の四角形ABCDと同じ面積の△ABEを作図しなさい。

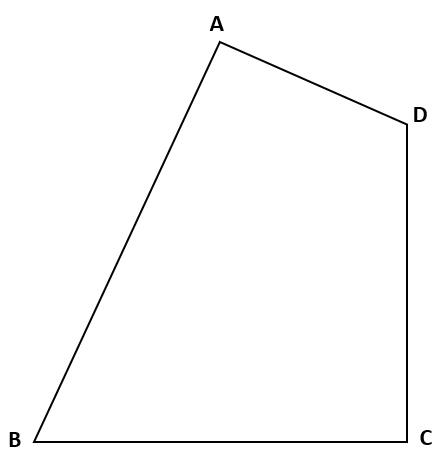
四角形のまま考えるのではなく、対角線を引いた時にできる三角形を変形して作図をするよ。
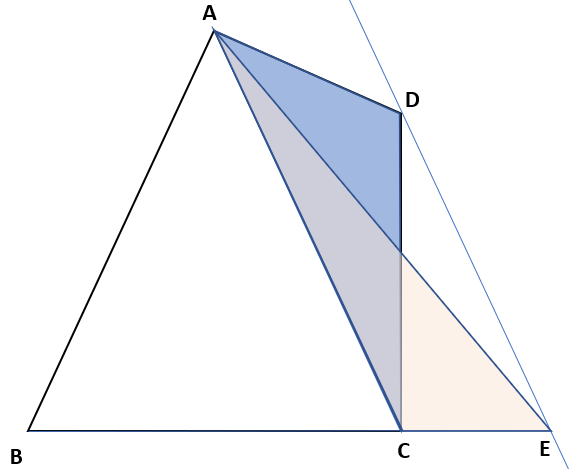
この問題では、下の図の色のついた三角形を変形しよう。

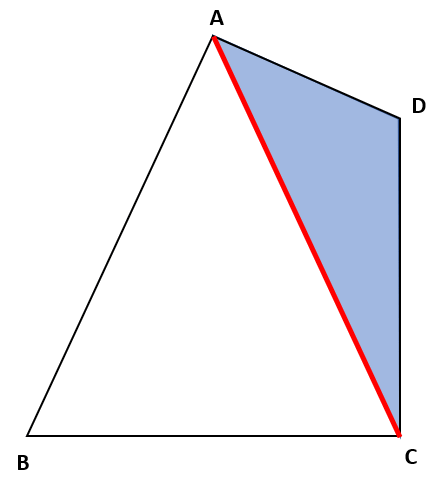
次に頂点Dを通り、対角線ACに平行な線を引くよ。
そして、その線とBCを延長した線との交点をEとするよ。

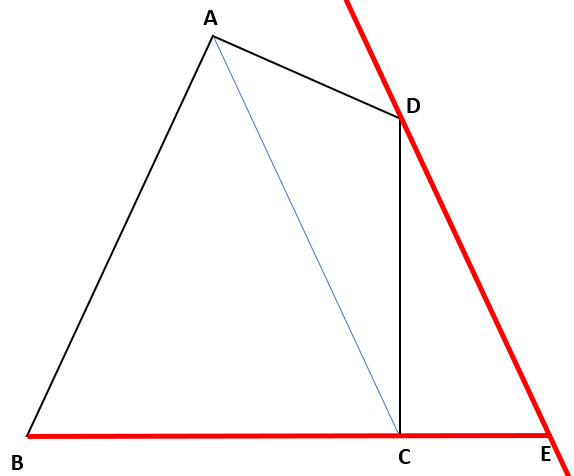
△ACDと△ACEは、平行な２つの線分の中にできる底辺がACの三角形だから、同じ面積になるよ。

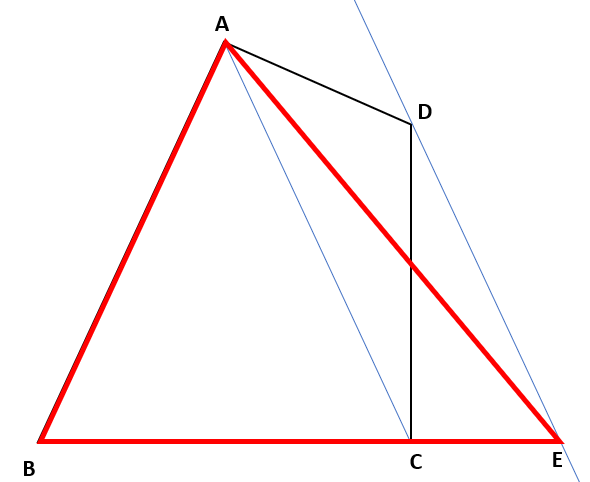
下の図の赤い線で囲まれた三角形が、四角形ABCDと同じ面積の△ABEだよ。

四角形の面積を変えずに三角形にする作図方法をまとめたから、解くときの参考にしてね。

四角形の面積を変えずに三角形にする作図方法

四角形の対角線を引く
四角形の１つの頂点を通り、①に平行な線を引く
②で引いた線と四角形の１辺を延長した線の交点を求める

作図問題は定期テストでも出題されるから、手順を忘れないように教科書やワークの問題にチャレンジしよう。

平行線と面積まとめ

平行な２つの線分の中にできる底辺が等しい三角形の面積は、等しくなる
四角形の面積を変えずに三角形にする作図方法
　①四角形の対角線を引く
　②四角形の１つの頂点を通り、①に平行な線を引く
　③②で引いた線と四角形の１辺を延長した線の交点を求める

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。