「多面体・正多面体」とは?種類と特徴一覧表(展開図つき)まとめ
中学1年生の数学で学習する「多面体・正多面体」について、どんな種類があるのかの一覧表、正多面体の定義と性質とは?正多面体の覚え方と、なぜ正多面体は5種類なのかなど、わかりやすく紹介しています。
正多面体の展開図をダウンロードすることもできます。
多面体とは
多面体とは、「平面だけで囲まれた立体」のことだよ。
例えば、サイコロなんかを想像したらわかりやすいと思うよ。
サイコロって6つの面が平らな面(平面)でできているよね。
逆に平面じゃないのは、缶ジュースやペットボトルなんかだね。
どちらとも周りは「曲がった面(曲面)」でできているよね。
多面体とは
平面で囲まれた立体のこと(例:サイコロ)
その多面体を作っている「面の数」によって名前が変わるよ。
四面体 五面体 六面体
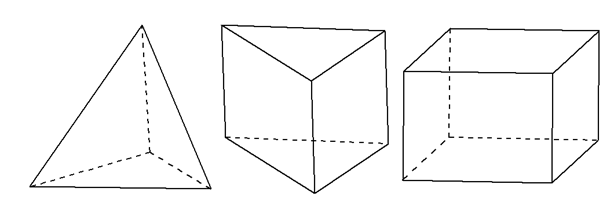
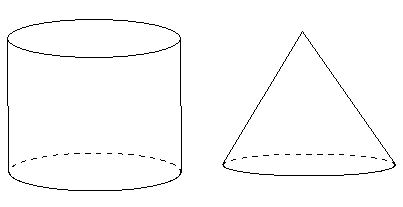
多面体ではないものの例は下図のようなものだよ。
両方とも曲がった面(曲面)で囲まれているよね。
正多面体の種類
多面体とはどういうものかわかったかな?
多面体には、実はさらに「正多面体」というものがあるんだ。
小学校でも「正三角形」「正方形」「正五角形」「正○○○」なんかを学習したよね。
「三角形」の仲間の中に、さらに「正三角形」があったり、「四角形」の仲間の中に、さらに「正方形」があったりしたのと同じ。
「正三角形」「正方形」「正五角形」「正○○○」というのは、すべての辺が同じ長さだとそう呼ばれるんだったよね。
中1で学習する「正多面体」は、「すべての面が同じになる立体」のことなんだ。
それでは実際に正多面体の図を見てみよう。
正多面体の図
正多面体を紹介するね。すべての面が同じになっていることがわかるかな?
正四面体
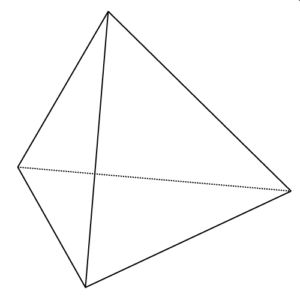
正四面体は、「同じ形の正三角形」の、「四つの面」でできている立体だよ。
正六面体
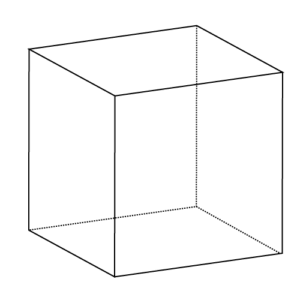
正六面体は、「同じ形の正方形」の、「六つの面」でできている立体だよ。
正八面体
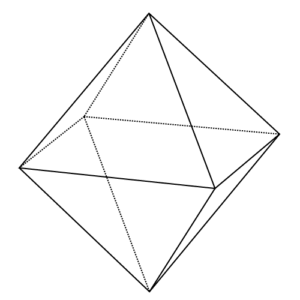
正八面体は、「同じ形の正三角形」の、「八つの面」でできている立体だよ。
正十二面体
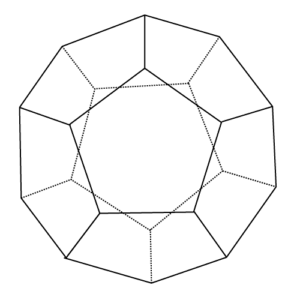
正十二面体は、「同じ形の正五角形」の、「十二の面」でできている立体だよ。
正二十面体

正二十面体は、「同じ形の三角形」の、「二十の面」でできている立体だよ。
正多面体の一覧表
正多面体は5種類しか存在しないんだ。
正多面体の面の形や面の数などを下の表にまとめたよ。
なぜ「5種類しか存在しないのか」は、あとで詳しく説明するので安心してね。
| 正多面体の名 | 面の形 | 頂点の数 | 辺の数 | 面の数 |
|---|---|---|---|---|
| 正四面体 (せいしめんたい) | 正三角形 | 4 | 6 | 4 |
| 正六面体 (せいろくめんたい) | 正方形 | 8 | 12 | 6 |
| 正八面体 (せいはちめんたい) | 正三角形 | 6 | 12 | 8 |
| 正十二面体 (せいじゅうにめんたい) | 正五角形 | 20 | 30 | 12 |
| 正二十面体 (せいにじゅうめんたい) | 正三角形 | 12 | 30 | 20 |
5種類とも、面の形が「正○○形」になっているね。
正多面体の定義(特徴)
正多面体とは、「すべての面が同じ」と説明したけれど、実はこの表現では少し”あいまい”なんだ。
正多面体にはきちんとした定義と呼ばれる特徴が2つあるんだよ。
この2つの特徴を満たしてこそ正多面体ということになるんだ。
正多面体の定義
- ①どの面もすべて合同な正多角形である。
- ②どの頂点にも面が同じ数だけ集まっている。
正直、これを聞いただけではピンとこないよね。
だけれど、①はなんとなく理解できるんじゃないかな?
「①どの面もすべて合同な正多角形である」
というのは、すべての面が合同な正多角形ということだよね。
一覧表にもあったけれど、すべての正多面体は「正三角形」・「正方形」・「正五角形」のどれかで囲まれていたよね。
「②どの頂点にも面が同じ数だけ集まっている」については立方体を例に考えてみよう。
立方体は正多面体なのか?
実際に立方体が正多面体かどうかを調べてみよう。
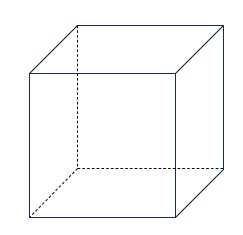
正多面体の定義に合っているかチェック!
☑どの面もすべて合同な正多角形である。
→すべての面が「正方形」になっている。(OK!)
☑どの頂点にも面が同じ数だけ集まっている。
→どの頂点にも3つの面が集まっている。(OK!)
2つの条件をクリアしているから、立方体は「正多面体」だよ。
どの頂点にも3つの面が集まっているってどういうこと?
たとえば、下の赤い点に注目してみよう。
ここが「頂点」だよ。(頂点はたくさんあるんだけれど、例として一つだけを赤い点にしているよ)
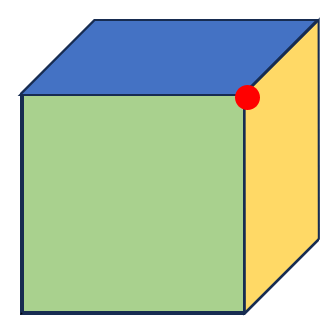
この頂点を含んでいる平面は色の付けたところ3つになるよね。
「頂点を含んでいる面」や「頂点に接している面」を「頂点に面が集まっている」と表現しているんだね。
図で確認するとわかりやすいね。
この「頂点に3つの面が集まっている」かどうかは、他の頂点で試してもやっぱり同じ状態になっているよ。
だから、「どの頂点にも3つの面が集まっている」と言えるんだね。
このように、正多面体の2つの条件を満たしているから、立方体は正多面体といえるんだね。
正多面体のように見えるけれど、正多面体ではない「六面体」
下図のような「六面体」という立体は、すべて合同な正三角形で囲われているよ。
そうすると、ぱっと見た感じでは「正多面体なのかな」と思ってしまうね。
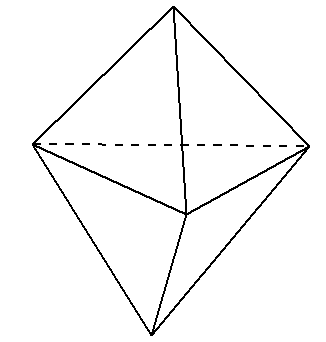
でも、1つの頂点に集まっている面の数を確認してみよう。
頂点によって、集まっている面の数は「3つ」とか「4つ」になってしまって、バラバラなんだ。
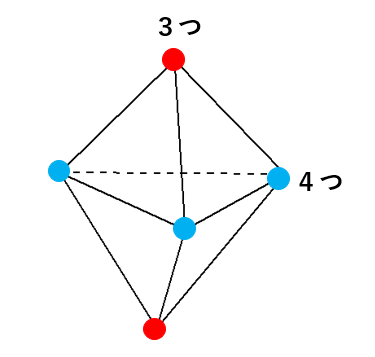
だから、正多面体の定義の①はクリアしているんだけれど、②がクリアできていないから、「六面体」は正多面体ではないんだよ。
正多面体かどうかを判断する時は、正多面体の定義2つともをクリアしているかをちゃんと確認しよう。
正多面体の定義(おさらい)
- ①どの面もすべて合同な正多角形である。
- ②どの頂点にも面が同じ数だけ集まっている。
オイラーの多面体定理とは
多面体には実はすごい性質があるんだ。
18世紀の数学者オイラーが発見した性質で、それを「オイラーの多面体定理」というよ。
さっきの表を見てみよう。
| 正多面体の名 | 面の形 | 頂点の数 | 辺の数 | 面の数 |
|---|---|---|---|---|
| 正四面体 (せいしめんたい) | 正三角形 | 4 | 6 | 4 |
| 正六面体 (せいろくめんたい) | 正方形 | 8 | 12 | 6 |
| 正八面体 (せいはちめんたい) | 正三角形 | 6 | 12 | 8 |
| 正十二面体 (せいじゅうにめんたい) | 正五角形 | 20 | 30 | 12 |
| 正二十面体 (せいにじゅうめんたい) | 正三角形 | 12 | 30 | 20 |
オイラーが発見したのは、多面体において、以下の計算式が成り立つということ。
オイラーの多面体定理
(頂点の数)−(辺の数)+(面の数)=2
本当にこんな計算式が成り立っているのかな?
例えば、正四面体で計算して確かめてみよう。
(頂点の数)−(辺の数)+(面の数)
=4−6+4
=2
確かに「2」になっているね。
正六面体でも計算してみよう。
(頂点の数)−(辺の数)+(面の数)
=8−12+6
=2
これも「2」になっているね。
多面体ってふしぎな性質を持っているんだね。
この「オイラーの多面体定理」を覚えておくと、「頂点の数」「辺の数」「面の数」のどれか2つが分かれば、残りの1つも計算すれば分かるということだね。
これを知らないと、問題に出てきたときに、実際に頭の中か紙にその多面体の立体図を描かないとわからない、なんてことになってしまうね。
四面体くらいだったらなんとかなるかもしれないけれど、二十面体なんて言われてしまったら、大変だよね。
ぜひ覚えておこうね。
正多面体の覚え方(語呂合わせ)
多面体はいっぱい種類があるけれど、「正」多面体となると5種類しか存在しないんだよ。
テストで「正多面体5種類答えなさい」という問題が出たときに、ぱっと答えられるように、語呂合わせを紹介するね。
正多面体の覚え方①
「よーろっぱじゅうに20ある」
正四面体(よー)
正六面体(ろっ)
正八面体(ぱ)
正十二面体(じゅうに)
正二十面体(20)
※最近だと、「20」のところをアイドルグループの「NiziU」で覚えても面白いね。
正多面体の覚え方②
「二十歳になったらじゆう(じゅうに)にしろや」
正二十面体(二十)
正十二面体(じゅうに)
正四面体(し)
正六面体(ろ)
正八面体(や)
正多面体はなぜ5種類なのか?
今まで多面体や正多面体を学習してきて、こんな疑問をもった人はいないかな?
「正多面体はなぜ5種類しかないのか?」
すごくいい疑問だと思うから説明していくね。
STEP1 正多面体とは何か
正多面体の定義は次の通りだったよね。
正多面体とは
①どの面もすべて合同な正多角形である。
②どの頂点にも面が同じ数だけ集まっている。
STEP2 正多面体の定義に1言追加
追加したいのは、
②どの頂点にも面が3つ以上の同じ数だけ集まっている。
ということ。
難しいことを言っているかもしれないけれど、当たり前のことなんだよ。
なぜなら、どんな立体でも1つの頂点に面が3つ以上でないと立体の角を作ることはできないよね。
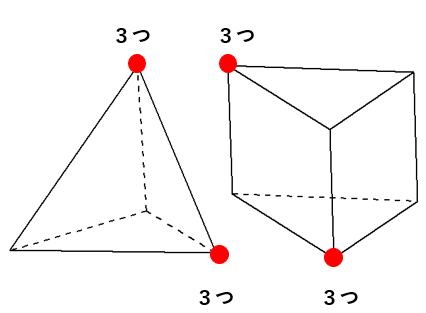
自分で立体を描いてみたらわかると思うよ。
1つの頂点に面が2枚の立体なんて描けない思うよ。
だから正多面体の定義は次のようになるよ。
正多面体とは
①どの面もすべて合同な正多角形である。
②どの頂点にも面が3つ以上の同じ数だけ集まっている。
ここまでは大丈夫かな?
それでは、この正多面体の定義を使って、なぜ5種類しかないかを説明するね。
STEP3 正四面体・正八面体・正二十面体の展開図を考えよう
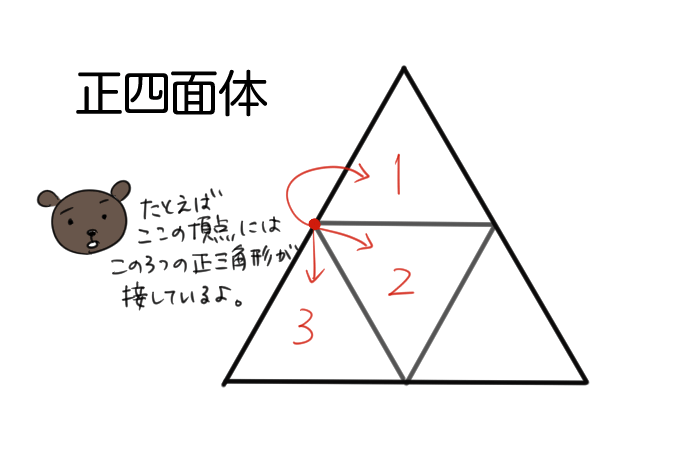
まず正四面体で考えよう。

上の頂点の周りの展開図は次の通りになるよね。
1つの頂点の周りに正三角形の面が3枚接していることがわかるね。
次に正八面体で考えよう。

1つの頂点の周りの展開図は次のようになるね。
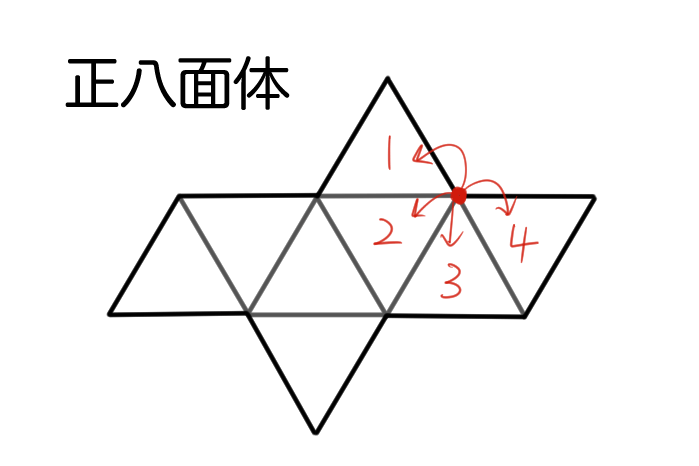
1つの頂点の周りに正三角形が4枚あることがわかるね。
次に正二十面体を考えよう。

1つの頂点の周りの展開図は次のようになるね。
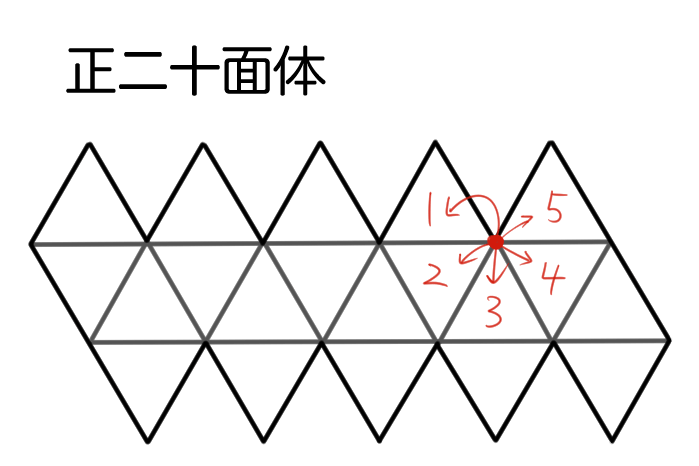
1つの頂点の周りに正三角形が5枚あることがわかるね。
正四面体・正八面体・正二十面体の展開図

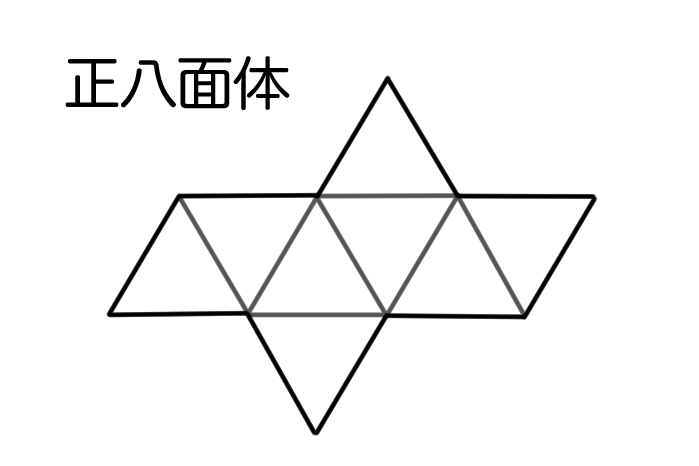
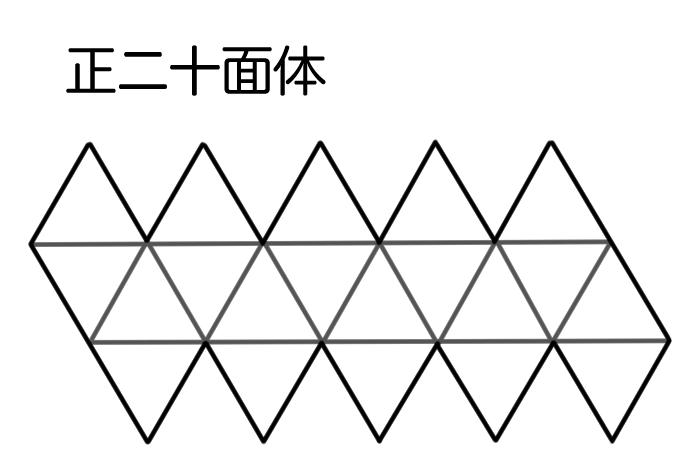
1つの頂点の周りに3~5枚の正三角形があることがわかるね。
1つの頂点の周りに集まる正三角形の数が「3」枚、「4」枚、「5」枚とくれば、こんなふうに予想する人もいるんじゃないかな?
予想
次は1つの頂点の周りに6枚の正三角形ができる正多面体になるのかな?
回答
1つの頂点の周りに6枚の正三角形ができる立体は作れないよ。
実際に1つの頂点の周りに6枚の正三角形があったとすると、次のようになるよ。
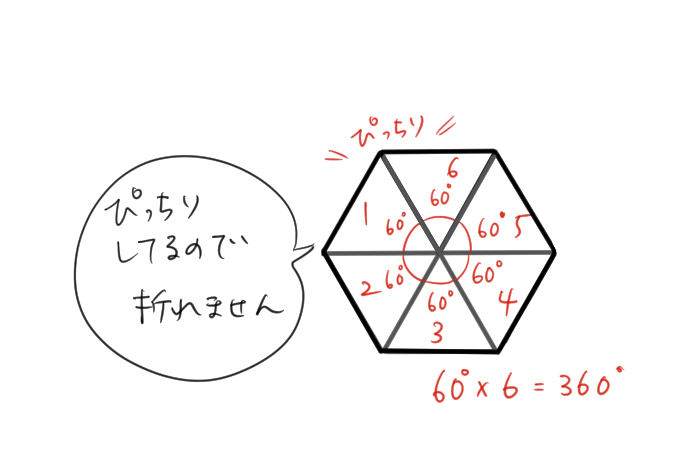
正三角形の1つの角度が60°だから6枚あると、60×6=360°でぴったり1周分になるね。
ただ、これでは「立体は作れない」よ。
だって「すき間」がないと折れないから立体はできないんだ。
試しに、一枚の紙を折って、その部分を頂点にして立体を作ろうとしてみて。
一部を重ねたり、切り取ったりして「すき間」を作らないと立体にはならないはずだよ。
だから、1つの頂点の周りに6枚の正三角形がある立体は作ることができないんだ。
ほかには、「3枚」「4枚」「5枚」があるなら、「2枚」もあるのでは?という疑問も出てくるかもしれないね。
疑問
1つの頂点の周りに2枚の正三角形ができる正多面体はないの?
回答
これはさっきも説明したね。2枚の面だけでは、そもそも「立体」はできないよね。
これらのことから、1つの頂点の周りに正三角形ができる正多面体は、1つの頂点に3つの正三角形が集まる「正四面体」・1つの頂点に4つの正三角形が集まる「正八面体」・1つの頂点に5つの正三角形が集まる「正二十面体」しか存在しないんだよ。
同じように他の正多面体も考えていくよ。
STEP4 正六面体の展開図を考えよう

1つの頂点の周りの展開図は次のようになるね。
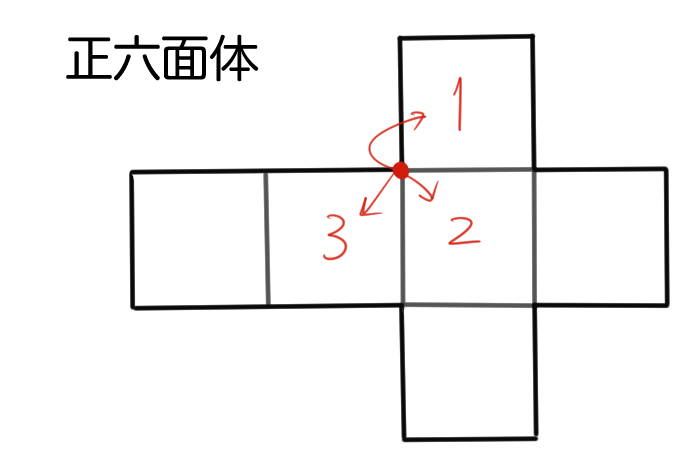
1つの頂点の周りに正方形が3枚あることがわかるね。正方形って1つの角度が90°だから、3枚だったら90×3=270°になるね。
ただ、4枚になると90×4=360°で、ぴったり1周分になってしまうね。
これでは、さっき説明したとおり立体は作れないよ。
だってすき間がないと折れないから立体はできないからね。
つまり、1つの頂点の周りに4枚の正方形ができるなんてことはありえない。
もちろん、2枚の正方形でも立体にはならない。
つまり、「3枚の正方形が集まった」立体しか存在しないんだ。
これらのことから、1つの頂点の周りに正方形ができる正多面体は、1つの頂点に3つの正方形が集まる「正六面体」しか存在しないんだよ。
STEP5 正十二面体を考えよう

1つの頂点の周りの展開図は次のようになるね。
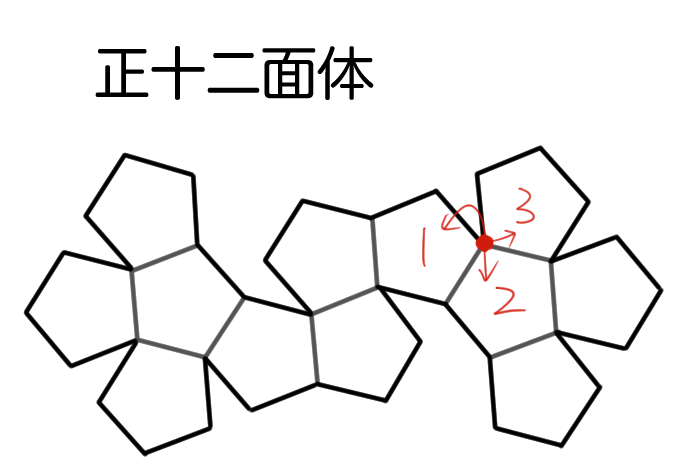
1つの頂点の周りに正五角形が3枚あることがわかるね。正五角形は1つの内角の角度が108°だから、3枚だったら108×3=324°。
360°よりも小さいから、すき間がちゃんとできるね。
ただ、4枚になってしまうと108×4=432°になっちゃうよね。360°を超えるから、立体にはならなくなってしまうね。
それどころか、描ききることさえできないね。
つまり、1つの頂点の周りに4枚の正五角形ができるなんてことはありえないよ。
もちろん、2枚の正五角形でも立体にはならないね。
これらのことから、1つの頂点の周りに正五角形ができる正多面体は、1つの頂点に3つの正五角形が集まる「正十二面体」しか存在しないんだよ。
STEP6 STEP3~5をまとめる
今までのことから次のことがわかったよ。
1つの頂点の周りに正三角形ができる正多面体は、正四面体・正八面体・正二十面体しか存在しない。
1つの頂点の周りに正方形ができる正多面体は、正六面体しか存在しない。
1つの頂点の周りに正五角形ができる正多面体は、正十二面体しか存在しない。
だから正多面体は5種類しか存在しなんだね。
おまけ:正六角形で囲まれた正多角形は存在しない
実は正六角形で囲まれた正多角形は存在しなんだよ。なんでかというと、正六角形の1つの内角の角度は120°。
もし1つの頂点の周りに正六角形が3つあったら、それだけで120×3=360°になってしまうんだ。360°は1周分だから、これでは、立体は作れないね。
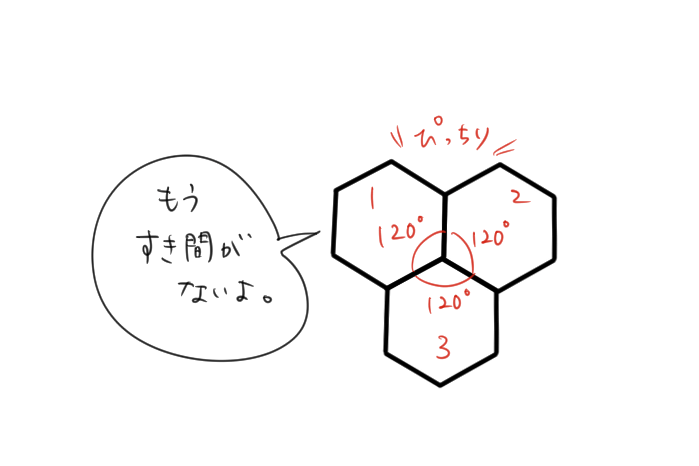
同じように、正七角形・正八角形で囲まれた正多角形というのも存在しないんだよ。3つ以上集まった時点で360°を余裕で超してしまうからね。
つまり、1つの頂点に正多角形が集まった時、360°を超してしまうかどうかがカギということだね。
多面体・正多面体の世界って、なかなか奥が深くて面白いね。
正多面体展開図一覧
正多面体の展開図を用意したよ。
ダウンロードもできるので、印刷して組み立ててみるのも面白いよ!
立体として実際に観察することで、もっとよく多面体・正多面体のことが理解できるといいな。
正四面体の展開図

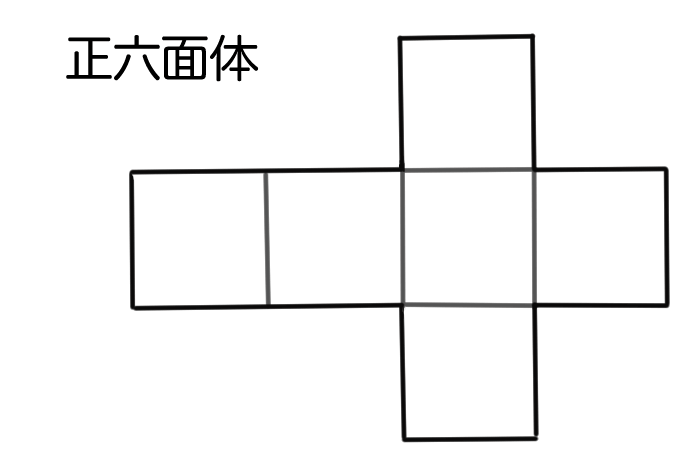
正六面体の展開図
正八面体の展開図

正十二面体の展開図
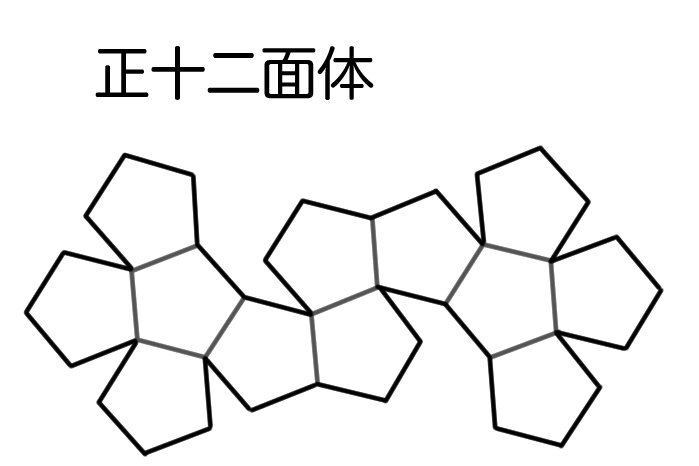
正二十面体の展開図

正多面体展開図ダウンロード
正四面体の展開図ダウンロード
正六面体の展開図のダウンロード
正八面体の展開図のダウンロード
正十二面体の展開図のダウンロード
正二十面体の展開図のダウンロード
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。

-
-
ご無沙汰してます。本年もよろしくお願いいたします。
正多面体が5種類しかない理由の説明すごくわかりやすいです。また、教えてください。
1,「正多面体」は、「すべての面が同じになる立体」とありますが、「すべての面の側辺の長さが等しい立体」ってことですよね?
2、三角錐と四面体についてです。
三角錐の定義では1つの三角形を底面とし、三角錐の頂点と底面の三角形の各頂点を結んでできる立体となっています。このことから次のようにいっていいのでしょうか?
(1)三角錐は四面体である。
三角錐は底面の三角形と側面の3つの三角形とからなるので、三角形の面が4つなので 四面体である。
(2)四面体は3角錐の一種である。
四面体のどれか一つの三角形を底面とみなせば三角錐として扱えるので三角錐の一種である。 -
定義ばかり質問して申し訳ないんですがまた教えてください。
中学数学で、空間図形、立体、平面図形という用語が出てきますが、この区別をどう考えればよいのか教えてください。以下は断片的には理解しているつもりですが頭の中がうまく整理できてません。
1、空間とは幅、長さ、奥行きの3つの方向(3次元)で構成される。
2、図形とは数学的には、形のあるものというより点の集合を指す。
3、空間図形というときは、空間上の点、直線、曲線、平面、曲面、立体などが含まれる。従って立体は空間図形の一部を指す。(立体とは?と聞かれるとどう説明すればいいのかはわかりません)
4,平面図形とは幅、長さをもつ2次元の平面上に、点の集合として直線や、曲線等で構成される形状を指す。独立変数が一つの1次関数や2次関数もグラフ化すれば平面図形となる。



四角錐、正四面体、三角錐もゴッチャになってしまう私…ですが
「正多面体」は、展開図を今回 描き写してみて 先生の説明がすんなり入りました
ありがとうございました