一次関数のグラフの特徴「切片」と「傾き」とは?わかりやすく解説
中学2年生の一次関数のグラフの特徴で学習する「切片」と「傾き」とは?
それぞれの言葉の意味と求め方を問題例をもとにしてわかりやすく解説するよ。
「切片」とは
これまで勉強してきた一次関数の式について、詳しく解説していくね。
まずは、y=aχ+bのbについて確認するよ。
bのことを数学の用語で切片っていうんだ。
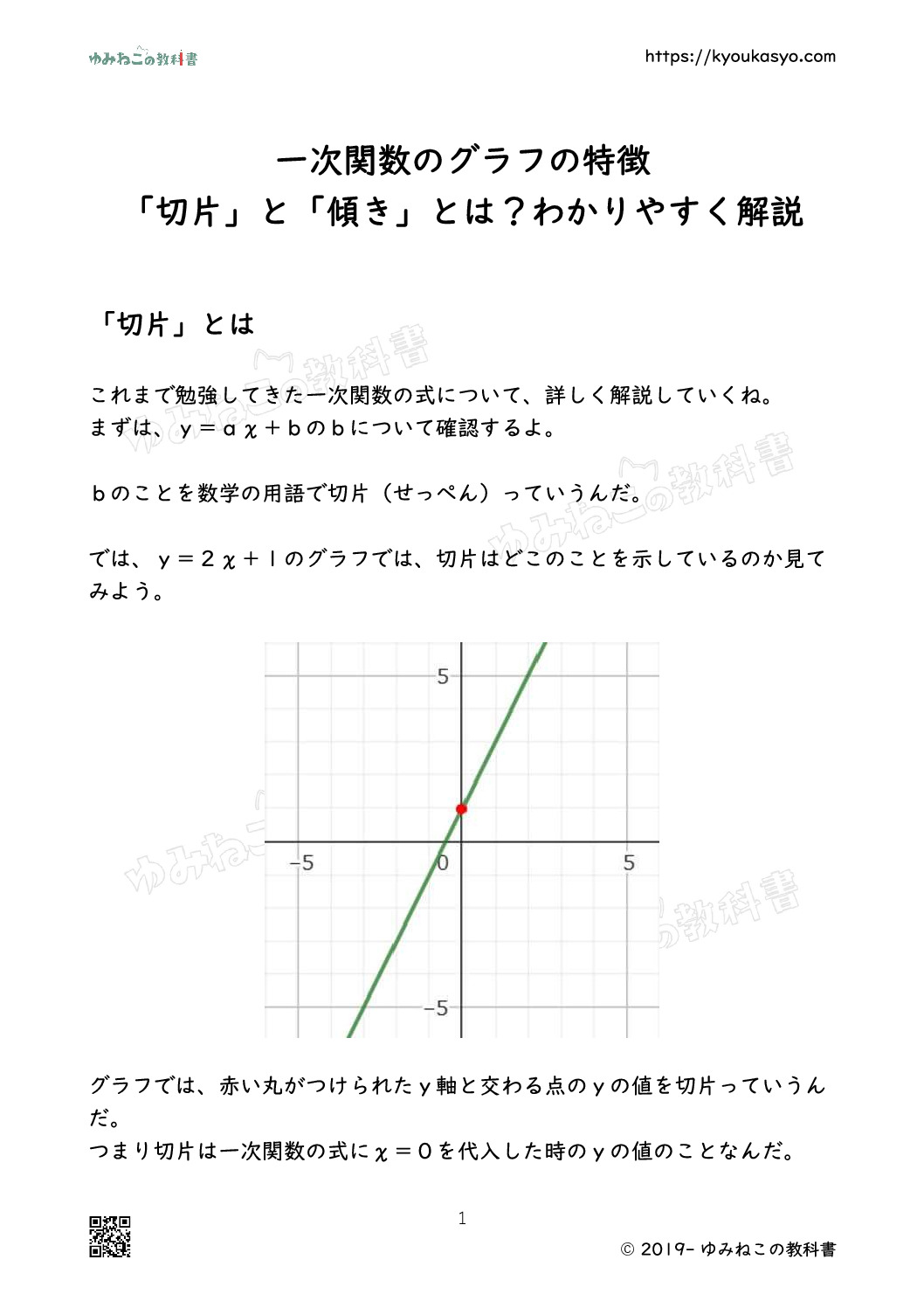
では、y=2χ+1のグラフでは、切片はどこのことを示しているのか見てみよう。
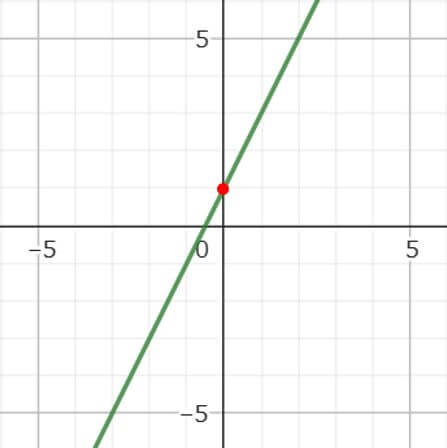
グラフでは、赤い丸がつけられたy軸と交わる点のyの値を切片っていうんだ。
つまり切片は一次関数の式にχ=0を代入した時のyの値のことなんだ。
y=2χ+1で実際にχ=0を代入してみると
y=2×0+1
y=1
と計算されて、bの値と同じになったね。
y=2χ-3のように、切片がマイナスになる時もあるよ。
問題
次の一次関数のy軸と交わる点の座標と切片を言いなさい。
座標は(χ、y)の形で答えなさい。
(1)y=-3χ+4
(2)y=5χ-8
y軸と交わる点、と聞くとついついy=0を代入したくなるよね。
さっきのy=2χ+1のグラフを見るとわかるとおり、χ=0の時だから注意しよう。
今回の問題は、
y軸と交わる点→y=aχ+bにχ=0を代入してyの値を求めて、その座標を答える
切片→式を見て、y=aχ+bのbの値を答える
という知識があれば簡単にできてしまう問題だよ。
(1)
y軸と交わる点
y=-3χ+4にχ=0を代入するとy=4となるね。
だから、y軸と交わる点の座標は(0、4)となるよ。
切片
グラフを見て、そのまま答えたらOKだよ。
切片は4
(2)
(1)と同じように解けばOKだよ。
y軸と交わる点は、(0、-8)
切片は-8
切片って慣れるまでは、どの部分かイメージしにくよね。
そこで、y軸を竹として、それを刀で斜めに切った姿をイメージしてみよう。
竹を刀で切った時に竹と刀が触れた点が切片、と覚えておくと少し覚えやすくなるかな。覚える時の参考にしてみてね。
「傾き」とは
次に傾きについて確認しよう。
y=aχ+bのaのことを傾きっていうんだ。
あれ?別な呼び方がなかった?と思った人もいるよね。
そのとおり!
aはいろんな呼び方があるから、改めて整理しよう。
y=aχ+bのaについて
①比例定数
②変化の割合
③傾き
今回の傾きを含めると、全部で3つの呼び方があるんだ。
傾きがどういうものかわかると、今後登場する一次関数のグラフを描く時やグラフから一次関数の式を求める時に役に立つから、その使い方について確認していこう。
傾きの使い方や性質について
①y=aχ+bのaを分数にして考えよう
②分数で表したら\(\frac{上下に進む数}{右に進む数}\)と考えよう
※分子がプラスの時は上に進んで、マイナスの時は下に進むよ。
この考え方を使って、y=2χ+1のグラフを見てみよう。
①aを分数にして考えよう
この式では、aは2だから、\(\frac{2}{1}\)として考えよう
②分数で表したら\(\frac{上下に進む数}{右に進む数}\)と考えよう
①から、
分母が1だから、右に1
分子が2だから、上に2
進むと考えよう。
じゃあ早速この考えを使って、グラフを見てみよう。
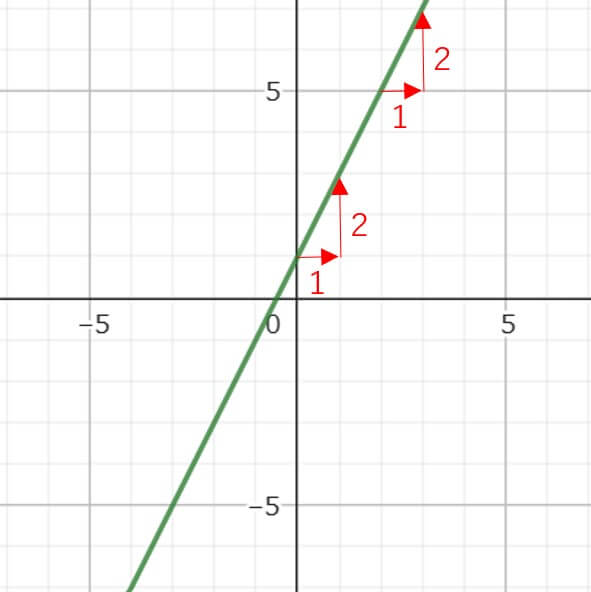
グラフを見てみると、
読み取りやすい点から、次の読み取りやすい点まで右に1進んで、上に2進んでいるよね。
傾きはこういう使い方ができるんだ。
では、y=-\(\frac{2}{3}\)χ+4のグラフで考えてみよう。
分数だから難しそう…って思うかもしれないけれど、さっきの手順で考えるとどんなグラフかすぐにわかるよ。
①aを分数にして考えよう
この式では、すでに分数だから気にする必要なし!
ただ、マイナスが付いているね。
マイナスは分子(上側の数字)に付いているから\(\frac{-2}{3}\)と考えよう。
②分数で表したら\(\frac{上下に進む数}{右に進む数}\)と考えよう
①から、
分母が3だから、右に3
分子が-2だから、下に2
進むと考えよう。
このグラフはこんな形になるよ。
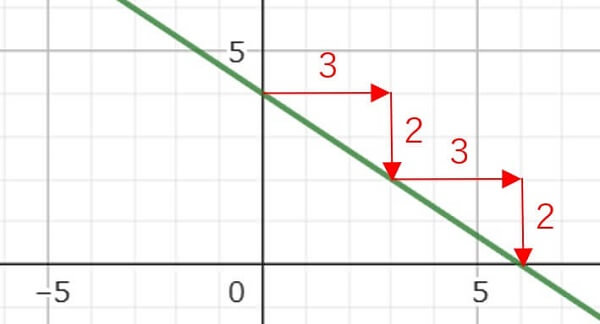
さっきのy=2χ+1のグラフと同じように、傾きの数字と合わせて見てみると
どこかの読み取りやすい点から、次の読み取りやすい点まで右に3進んで、下に2進んでいるよね。
傾きを使うと一次関数のグラフが簡単に描けるようになるから、ぜひ覚えておこう。
問題
次の(1)から(4)の傾きと切片を答えなさい。
(1)y=-3χ+3
(2)y=2χ-5
(3)y=-\(\frac{1}{2}\)χ+\(\frac{4}{5}\)
(4)y=6χ
それぞれ式を見たまま答えることができるね!
(1)傾き-3、切片3
(2)傾き2、切片-5
(3)傾き-\(\frac{1}{2}\)、切片\(\frac{4}{5}\)
(4)は少し迷った人がいるかな?
切片が書かれていない式なんだけれど、切片が0と考えよう。
傾き6、切片0
切片と傾きは、この後出てくる一次関数のグラフや一次関数の式を求める時によく出てくるから、それぞれの特徴をしっかりと覚えておこう!
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


例えば(ー5.0)でx軸と交わり、(0.3)でy軸と交わる場合、傾きはいくらになるのでしょうか。