「証明のやり方と書き方」のコツは？証明問題をわかりやすく解説

中学２年生の数学で学習する「証明」について、証明問題の解き方や考え方、証明のやり方や書き方をわかりやすく解説するよ。

よく使われる証明の根拠を一覧にまとめたものもあるので、確認してみよう！

「証明のやり方と書き方」のコツは？証明問題をわかりやすく解説のPDF（14枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

「角の二等分線」の作図を三角形の合同条件を使って証明してみよう

「証明」とは何かを学習してきたけれど、今回はいよいよ実際に「証明」することにチャレンジするよ。

言葉の使い方や用語など、証明にはやり方（書き方）にルールがあって、ちょっとややこしいんだ。

そこで、中学１年生で習った「角の二等分線」を例に「角の二等分線は、本当に角を二等分しているのか？」を証明してながら、証明のやり方や書き方を確認していこう。。

それでは、「下の図の∠XOYの二等分線」の作図を復習しながら解説していくよ。

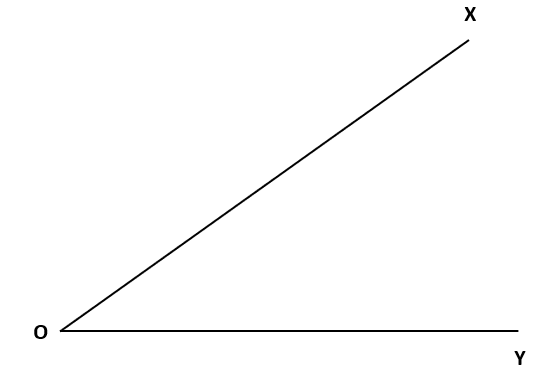
①点Oを中心とする円をかいて、辺OXと辺OYとの交点をA、Bとしよう。

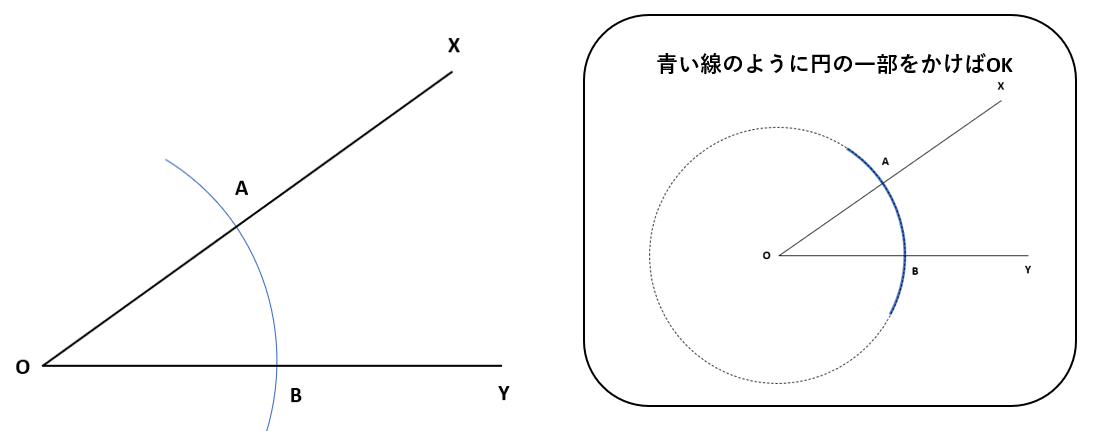
上の図のように、円は辺OXと辺OYと交わる部分だけでOKだよ。

②A、Bを中心とする等しい円をかいて、その交点をCとしよう。

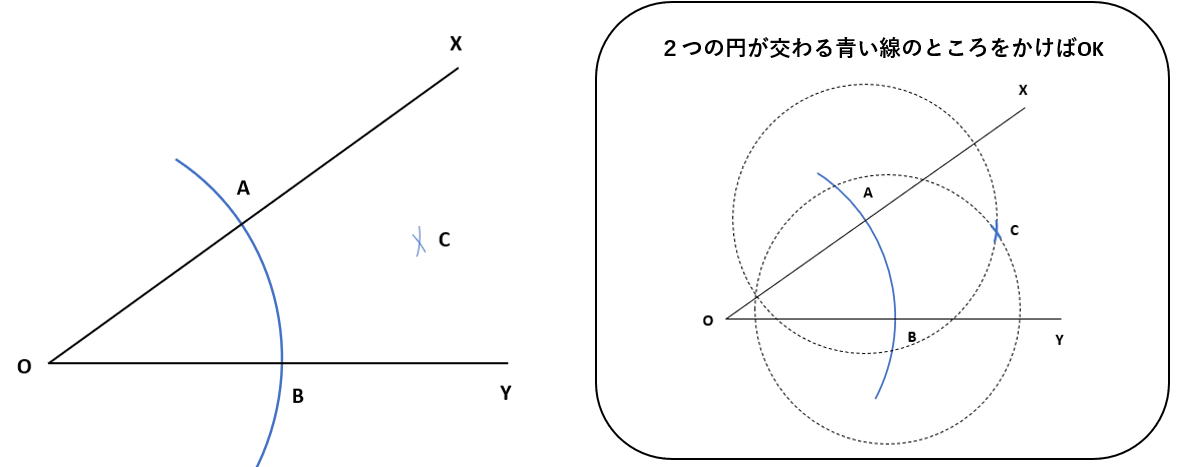
①の時と同じように、円は一部だけかけばOKだよ。

③半直線OCをひいて、角の二等分線の作図は完成だよ。

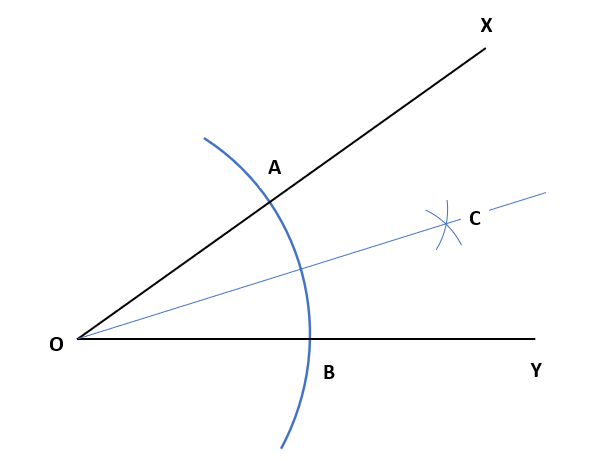
角の二等分線は、１つの角を二つに等しく分ける線のことなんだけれど、本当にOCが∠XOYを二つに等しく分けている線か証明を三角形の合同条件を使って確認してみよう。

まず、OCが角の二等分線になるということは、∠AOCと∠BOCが∠XOYの半分の大きさになっているということだから、
∠AOC＝∠BOC
ということが証明すればいいんだ。

ここで、∠AOCと∠BOCが同じ大きさということを証明するためには、下の図の△AOCと△BOCが合同であることを使って証明をするよ。

なぜ三角形の合同を使うのか？

角の大きさの証明なのに、なんで三角形の合同を使うのか疑問に思った人もいると思うから説明するね。

それは、△AOCと△BOCが合同だということが言えたら、∠AOCと∠BOCは２つの三角形でぴったり重なる部分になって、同じ大きさということがいえるから三角形の合同を使うんだ。

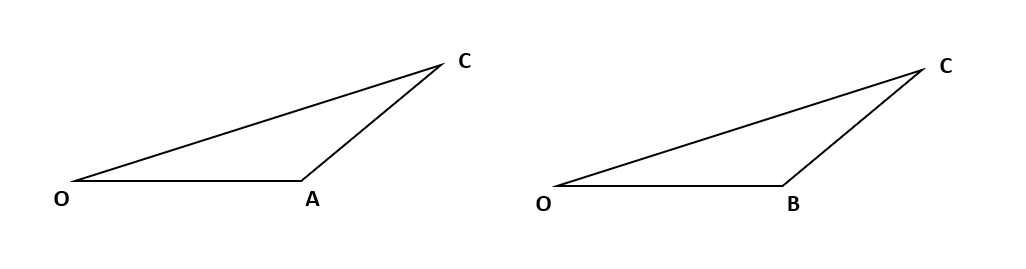
上の図のように、２つの三角形を頂点が対応する順にかくとイメージしやすくなるよ。

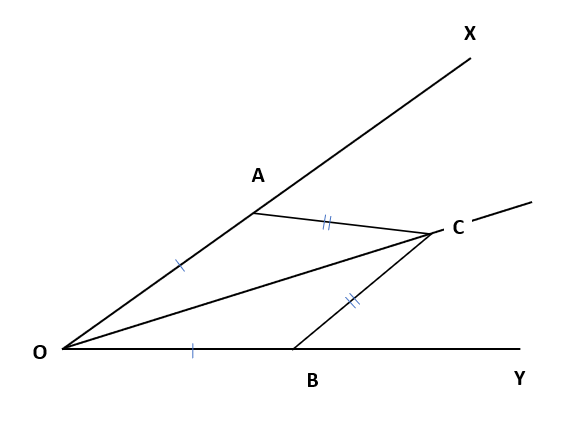
作図をしていく中で、同じ長さになることがわかるから上の図に印をつけたよ。

・OAとOBについて
AとBは、作図をする時にOを中心とする円をかいて見つけた点だったよね。
作図の手順の①を見てわかるとおり、OAとOBは円の半径になっているから、同じ長さになるだ。

だからOA＝OBということがいえるよ。

・ACとBCについて
次に、Cは作図手順の②を見てみると、AとBから等しい円をかいて見つけた点だったよね。
つまり、ACとBCは円の半径になるから、

だから、AC＝BCということがいえるよ。

・OCについて
そして最後に、OCを見てみよう。
これは、△AOCと△BOCの２つの三角形と重なっているから、同じ長さということがわかるね。

今の流れを整理して証明すると下のようになるよ。

△AOCと△BOCは
OA＝OB
AC＝BC
OC＝OC
で、３組の辺がそれぞれ等しいから
△AOC≡△BOC
合同な図形の対応する角は等しいから、
∠AOC＝∠BOC
したがって、OCは∠XOYの二等分線である

これで、角の二等分線について証明をすることができたよ。
ここから証明について、詳しく説明していくね。

「仮定」とは

まずは証明で使われる言葉について説明するね。

１つ目は、「仮定かてい」だよ。

証明の問題には、よく「●●●ならば」というフレーズがでてくるんだけれども、この「ならば」の前の「●●●」の部分が仮定だよ。

（例）
クマならば動物である。　仮定は、「クマ」
△ABC≡△DEFならば、∠ABC＝∠DEF　仮定は「△ABC≡△CEF」

証明の問題では、仮定をスタート地点として解き進めていくから、仮定がどの部分かを素早く見つけられるようにしよう。

「結論」とは

次に「結論けつろん」について説明するね。

さっきの仮定の続きで「●●●ならば□□□」というフレーズがでてくるんだけれども、「ならば」の後の「□□□」の部分が結論だよ。

（例）
クマならば動物である。　結論は「動物」
△ABC≡△DEFならば、∠ABC＝∠DEF　結論は「∠ABC＝∠DEF」

結論は証明するときのゴール地点になるものなんだ。
証明するときには、仮定と結論をセットで毎回確認しよう。

証明のすじ道の考え方

いよいよ証明問題の解き方について確認していくよ。
まずは、証明を解き始める前に、どうやって証明を解き進めていくかという「すじ道」を下の手順で考えていくよ。

証明の解き進める手順

仮定と結論を問題文から見つけよう。
仮定からわかることを書こう。
すでに正しいと認められていることがらを図形を見て探そう。
三角形の合同条件のどれに当てはまるかを考えよう。
結論が証明されたことを書こう。

例題を使って、証明のすじ道を考えて問題を解いてみよう。

例題
下の図は、線分ABとCDの交点をEとして、EA＝EB、AD∥CBならば、ED＝ECとなることを証明しなさい。

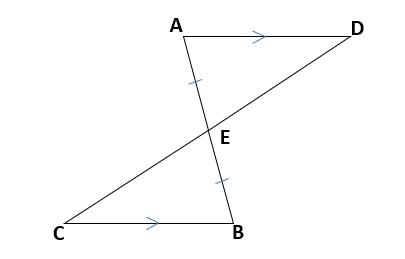
①仮定と結論を問題文から見つけよう。

問題文に「EA＝EB、AD∥CBならば、ED＝EC」と書いてあるから、仮定と結論を簡単に見つけることができるね。

仮定　EA＝EB、AD∥CB
結論　ED＝EC

また、仮定から結論を導くためには△AEDと△BECが合同であるといえたら、OKだよ。

【重要】
証明が苦手な人は、合同を証明する２つの三角形を同じ向きで書き抜くと対応する順や使う合同条件が見つけやすくなるよ。

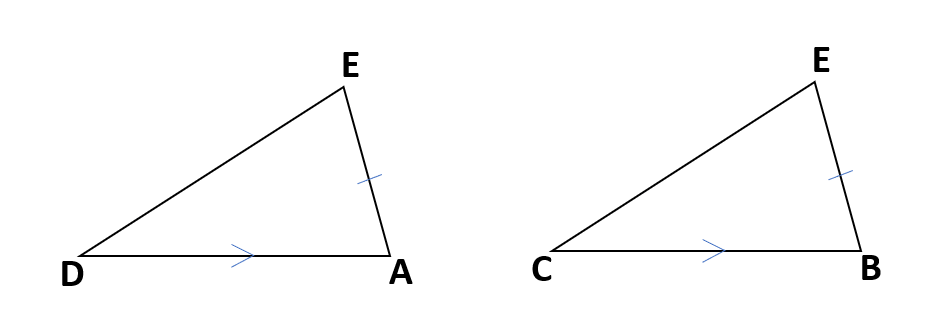
②仮定からわかることを書こう。

仮定からわかることは、

EA＝EB
AD∥CB

の２つなんだけれど、ここで注意が必要だよ。
AD∥CBのように、仮定で平行線が出てきた時には、問題文には書かれていない等しいものがあるんだ。

それは

平行線の錯角は等しい
平行線の同位角は等しい

という２つのことなんだ。

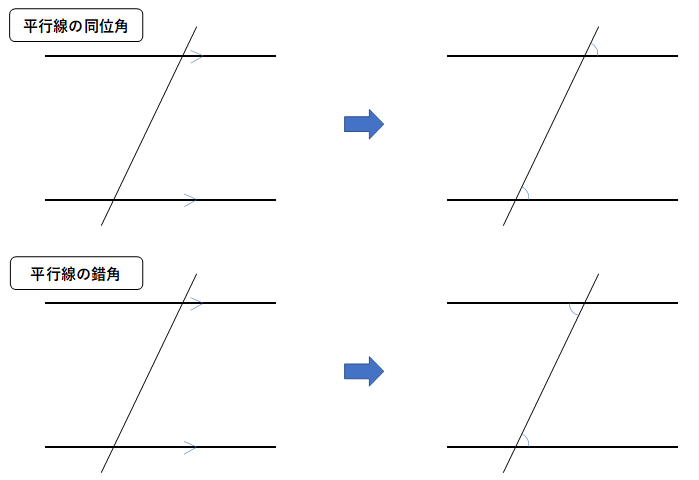
どちらを使うかは問題の図を見て考えるんだけれども、『平行線の錯角は等しい』という性質を使うことが多いよ。

今回の問題では

EA＝EB
AD∥CB⇒平行線の錯角は等しいので、∠EAD＝∠EBC、∠EDA＝∠ECB

ということがいえるよ。

③すでに正しいと認められていることがらを図形を見て探そう。

言葉だけを聞くと、どういうことか少しわかりにくいよね。
これは、図形の性質から絶対に正しいといえることを見つける、ということだよ。

今回の問題の図形では、対頂角が等しいという性質を使って
∠AED＝∠BEC

ということがいえるよ。

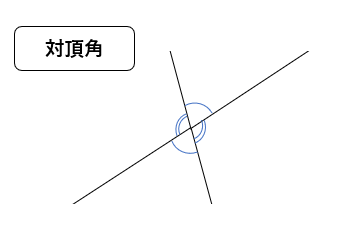
※証明の問題でよく使われる根拠の根拠・条件は一覧にして、このページの最後に書いてあるから確認していこう！

④三角形の合同条件のどれに当てはまるかを考えよう。

ここまで確認した２つの三角形の中で等しい所にマークをつけよう。

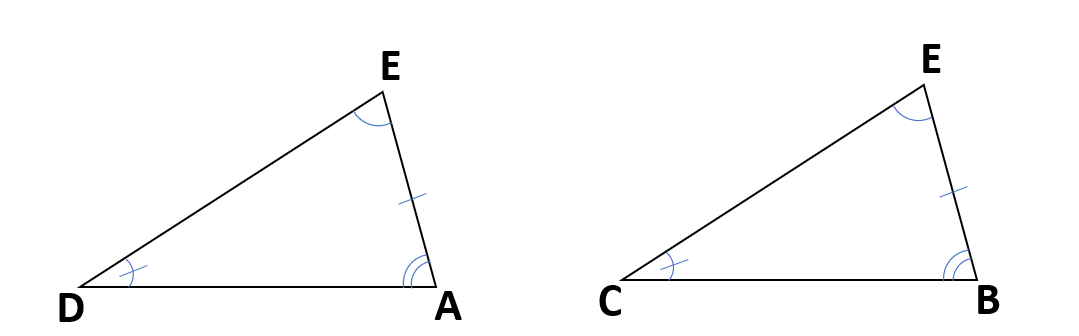
上の２つの三角形を見て、当てはまる合同条件を考えよう。
そうすると

１組の辺とその両端の角がそれぞれ等しい

に当てはまることがわかるね。
※∠EDAと∠ECBは大きさが等しいけれども、合同条件を考える時に必要ない角だから、証明を書くときには『∠EDA＝∠ECB』を書かないので注意しよう。

⑤結論が証明されたことを書こう。

これで２つの三角形が合同ということが証明できたから、最後の総仕上げ！
２つの三角形が合同だから、角や辺が等しいという時に使うフレーズがあるから、必ず覚えよう。

それは、

合同な図形の対応する辺は等しいから
合同な図形の対応する角は等しいから

というフレーズだよ。

今回は、ED＝ECを証明するから、『合同な図形の対応する辺は等しいから』というフレーズを使おう。

ここまで来たらあとは、これまでのことを整理して証明を書いていくよ。

例題の証明

△AEDと△BECにおいて
仮定から、EA＝EB・・・①
AD∥CBより平行線の錯角は等しいから、∠EAD＝∠EBC・・・②
対頂角は等しいから、∠AED＝∠BEC・・・③
①、②、③より、１組の辺とその両端の角がそれぞれ等しいから
△AED≡△BEC
合同な図形の対応する辺は等しいから
ED＝EC

証明は上のように解き進めていくんだ。

最初のうちは、証明でよく使われる『～において』や『合同な図形の対応する～』という言葉が書き慣れないかもしれないけれど、何度も問題にチャレンジしていくうちに覚えることができるから、諦めずに取り組もう！

また、穴埋め問題で演習をして慣れていくこともおすすめだよ。

よく使われる証明の根拠・条件一覧

対頂角の性質

対頂角は等しい

平行線の性質

２直線に１つの直線が交わるとき、

２直線が平行ならば、同位角は等しい
２直線が平行ならば、錯角は等しい

平行線になるための条件

２直線に１つの直線が交わるとき、

同位角が等しければ、その２直線は平行である
錯角が等しければ、その２直線は平行である

三角形の内角の性質

三角形の内角の和は１８０°である

三角形の外角の性質

三角形の外角は、それととなり合わない２つの内角の和に等しい

合同な図形の性質

合同な図形では、対応する線分は等しい
合同な図形では、対応する角は等しい

三角形の合同条件

３組の辺がそれぞれ等しい
２組の辺と、その間の角がそれぞれ等しい
１組みの辺と、その両端の角がそれぞれ等しい

「証明のやり方と書き方」まとめ

「証明のやり方と書き方」まとめ

証明の問題の「●●●ならば」の「ならば」の前の「●●●」の部分が仮定
仮定の続きで「●●●ならば□□□」の「ならば」の後の「□□□」の部分が結論