「yはxの二乗に比例する」関数とは？二次関数との違い・比例定数

中学３年生の数学で学習する「y=ax2（ｙはｘの二乗に比例する）」関数について、二乗に比例するとはどういう特徴をもっているのか、y=ax2（ｙはｘの二乗に比例する）の比例定数とは何かをくわしく解説するよ。

「yはxの二乗に比例する」関数とは？ 二次関数との違い・比例定数のPDFをダウンロード

「yはxの二乗に比例する」関数とは？ 二次関数との違い・比例定数

「yはxの二乗に比例する」関数とは？ 二次関数との違い・比例定数のPDF（6枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

yはxの二乗に比例する関数

「関数」とは、「xの値が1つ決まる」と、「yの値もただ1つ決まる」という関係のことだったよね。
※「関数」とは何かをわかりやすく解説しているページもあるよ

今まで、比例や反比例、一次関数などの関数を学習してきたね。

今まで学習してきた関数

・比例　y=ax

・反比例　y=\(\frac{a}{x}\)

・1次関数　y=ax+b

3年生の数学で学習するのは、「二乗に比例する関数」だよ。

二乗に比例する関数の身近な例

「二乗に比例する」と言われても、ちょっとピンとこないね。
実際の例をもとに説明していくよ。

たとえば、「坂道で球を転がしてみた時」を考えてみよう。
坂道で球を転がすと、だんだんスピードアップして転がり落ちていく（加速していく）よね。

坂を転がし始めてから、1秒ごとの球の位置を記録したら次のようになったよ。

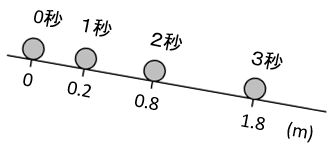
球が斜面を転がる様子
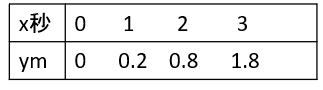
球が斜面を転がるときの時間と距離

この表を見ると

xが2倍、3倍、4倍・・・となるとyの値は4倍、9倍、16倍・・・となっているよね。

じゃあxとyの関係はどうなるだろう？
xとyだけの関係で考えると、

x=1のときは、y=0.2（y=0.2x）
x=2のときは、y=0.8（y=0.8x）
x=3のときは、y=1.8（y=1.8x）

・・・となってしまって、比例定数が定まらないね。
つまり、これは比例の関係ではないということだね。

そこで、さっきの表に「x2」を付け足してみるよ。

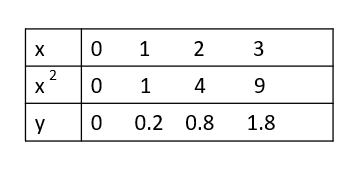
球が斜面を転がるときの時間ｘとｘ^2と距離ｙ

x２=1のときは、y=0.2（y=0.2x2）
x２=4のときは、y=0.8（y=0.2x2）
x２=9のときは、y=1.8（y=0.2x2）

比例定数が定まったね。
つまり、この表を見るとyの値はx2の値の0.2倍になっていることがわかるよね。

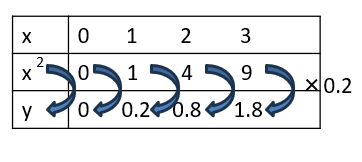
ｘ^2とｙの関係を表した表

だから
y=0.2x2
と表すことができるんだよ。

「y=0.2x2」という式からもわかるけれど、「yはxの二乗に比例する」関数になっているよね。

二乗に比例する関数の形

y=0.2x2は「yはxの二乗に比例する」関数だったよね。

「yはxの二乗に比例する」関数の形を紹介しよう。

yはxの二乗に比例する関数

  • y=ax2で表すことができる
  • 「a」のことを比例定数と呼ぶ
  • 比例定数「a」はa=\(\frac{y}{x^2}\)で求めることができる
    ※ただし、この式は「y=ax2」の両辺を「x2」で割ったら出てくるので、絶対に覚える必要はないよ。

「２次関数」と「ｙはｘの二乗に比例する関数」の違い

２年生で「1次関数」を学習したから、３年生で学習したこの「y=ax2」のことは「２次関数」とは言わないの？と思う人も多いかもしれないね。

「２次関数」と「ｙはｘの二乗に比例する関数」の違いを説明するよ。

２次関数と二乗に比例する関数の違い

  • ２次関数は「y=ax2+bx+c」
  • ｙはｘの二乗に比例する関数は「y=ax2」

ｙはｘの二乗に比例する関数「y=ax2」っていうのは、

２次関数「y=ax2+bx+c」の式で、b=0、c=0になる特別な場合のことなんだよ。

こんな感じのイメージだね。

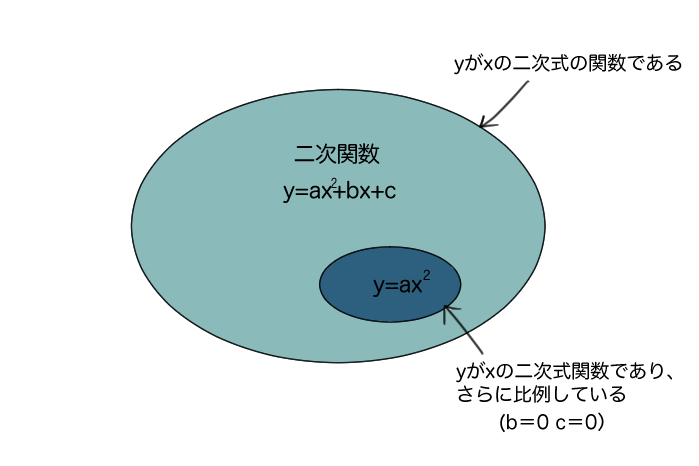
二次関数と、yがxの二乗に比例している関数の関係を表しているイラスト

２次関数という集まりの中に、「ｙはｘの二乗に比例する関数」がいるということだね。
だから、「ｙはｘの二乗に比例する関数」は、２次関数といっても間違いではないけれど、中学3年生でやるのは、b=0、c=0の特別な場合（＝比例している）だけだよ。

y=ax²の比例定数の求め方

ｙはｘの二乗に比例する関数「y=ax2」の比例定数「a」の値を次の問題で求めてみよう。

(1)

1辺がxcmの正方形で、高さが4cmの四角柱の体積がycm3になった。yをxの式で表せ。

また比例定数を答えなさい。

直方体

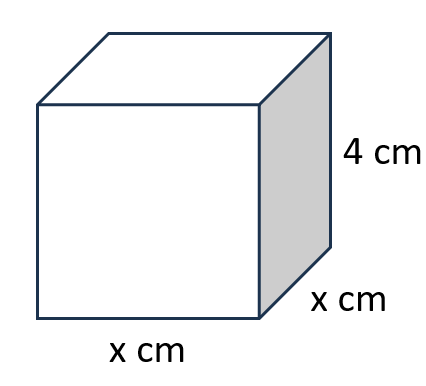
四角柱の体積は

体積＝底面積×高さ

で求まるから、

y=x×x×4
y=4x2

と表すことができるよね。

だから比例定数は「4」になるね。

(2)

yはx2に比例し、x=2のときy=12になる。yをxの式で表せ。

この問題はよく入試問題や定期試験にでるよ。

まず、「yはx2に比例し」という文章を見たら、

「ｙはｘの二乗に比例する関数だから、答えの式は、y=ax2になるな」と反応できるようにしよう。

これができたら、あとは楽勝だよ。

y=ax2に「x=2のときy=12」を代入しよう。

12=a×22

12=4a

a=3

比例定数「a」が「3」とわかったので、「y=ax2」の式に代入しよう。

答えの式は

y=3x2

と求めることができるよ。

「ｙはｘの二乗に比例する関数」まとめ

「ｙはｘの二乗に比例する関数」まとめ

  • 「ｙはｘの二乗に比例する関数」の式は、「y=ax2」で表すことができる
  • 「a」のことを比例定数と呼ぶ
  • 比例定数「a」はa=\(\frac{y}{x^2}\)で求めることができる
  • ｙはｘの二乗に比例する関数「y=ax2」とは、２次関数「y=ax2+bx+c」の式で、b=0、c=0になる特別な場合のことである

運営者情報

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。

感想や意見を聞かせてね