「箱ひげ図」と「ヒストグラム」の違いと特徴をわかりやすく解説
中学校2年生の数学で学習する「箱ひげ図」について、ヒストグラムとの違いをわかりやすく解説するよ。
それぞれの特徴とメリット・デメリットを考えて、「箱ひげ図」と「ヒストグラム」、それぞれがどのようなデータを表すときに適しているのかを紹介するよ。
「ヒストグラム」の復習
中学1年生の時に習った「ヒストグラム」について覚えているかな?
「箱ひげ図」と「ヒストグラム」を対応させる前に、まずは「ヒストグラム」の読み取り方や中央値の求め方などを復習しよう。
例題
下のヒストグラムは、あるクラスの身長のデータを元に作られたものである。
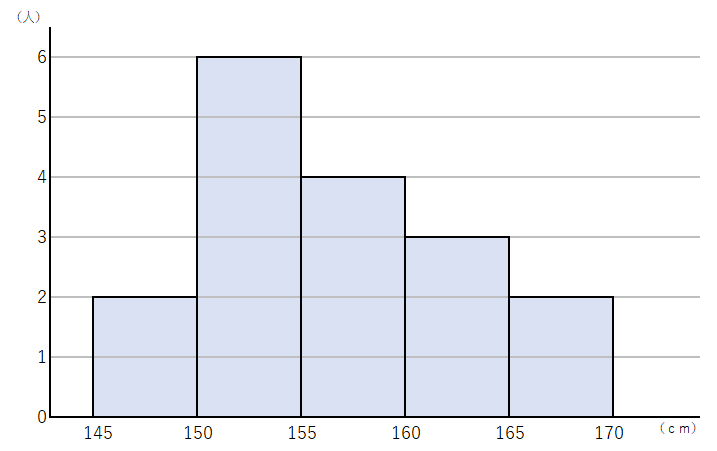
階級の幅・階級値・度数・最頻値・中央値・平均値をそれぞれ答えなさい。
※平均値は、小数第一位まで求めなさい。
「階級」について
階級は、グラフの横軸の区間のことだよ。
このヒストグラムの階級は、下のようになるよ。
「145cm以上150cm未満」
「150cm以上155cm未満」
「155cm以上160cm未満」
「160cm以上165cm未満」
「165cm以上170cm未満」
※「以上」はその数字が含まれ、「未満」はその数字が含まれない
145cm以上の場合、145cmは含まれる
150cm未満の場合は、150cmは含まれない
「階級値」について
階級値は、階級の中央の値のことで、計算して求める必要があるよ。
階級値を求める式
\(\frac{階級の端の数字+階級の端の数字}{2}\)
145cm以上150cm未満の階級値は、上の公式に代入すると
\(\frac{145+150}{2}\)=147.5
と求めることができるよ。
| 階級 | 階級値 |
| 145cm以上150cm未満 | 147.5 |
| 150cm以上155cm未満 | 152.5 |
| 155cm以上160cm未満 | 157.5 |
| 160cm以上165cm未満 | 162.5 |
| 165cm以上170cm未満 | 167.5 |
度数について
度数は、1つ1つの階級に含まれるデータの個数のことだよ。
この例題では、各階級に何人いるかを数えるだけだから、数え間違いをしないように注意しよう。
| 階級 | 度数 |
| 145cm以上150cm未満 | 2 |
| 150cm以上155cm未満 | 6 |
| 155cm以上160cm未満 | 4 |
| 160cm以上165cm未満 | 3 |
| 165cm以上170cm未満 | 2 |
最頻値について
最頻値は、「最も頻繁にあらわれる値」のことで、度数が一番多い階級値のことだよ。
今回の例題では、一番多い度数は、「150cm以上155cm未満」の6だから、最頻値は157.5となるね。
中央値について
中央値は、データを値の大きさの順にならべた時に、中央(真ん中)の位置にくる階級値のことだよ。
この例題では、17人分のデータがあるから、中央(真ん中)の位置にくるのは9番目の値ということがわかるね。
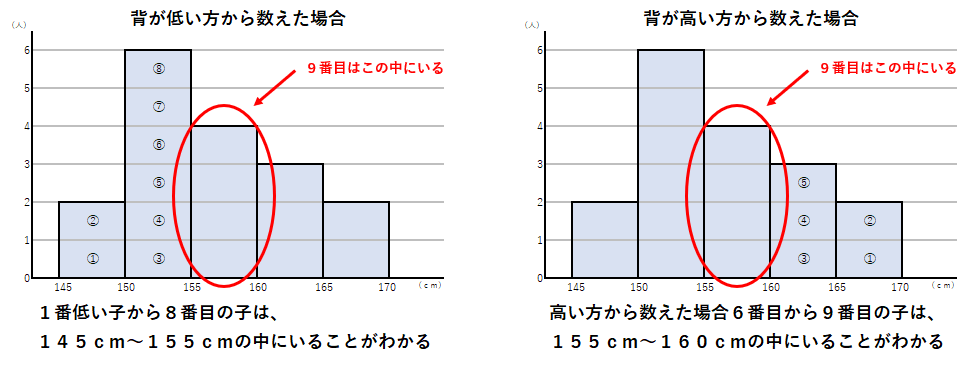
9番目の値は、「155cm以上160cm未満」の度数のところにあるから、中央値は157.5となるよ。
平均値について
ヒストグラムから平均値を求める時は、下の公式を使って求めるよ。
ヒストグラムを使った平均値を求める公式
平均値=\(\frac{(各階級値×度数)の合計}{度数の合計}\)
今回の問題では、
\(\frac{147.5×2+152.5×6+157.5×4+162.5×3+167.5×2}{17}\)=156.61
となるから、平均値は小数第二位を四捨五入して156.6となるね。
「箱ひげ図」と「ヒストグラム」を対応させてみよう
ここからいよいよ、「箱ひげ図」と「ヒストグラム」を対応させてみよう。
例題
次の点数は、あるクラスの11人の数学の点数である。
| A | B | C | D | E | F | G | H | I | J | K |
| 8 | 7 | 1 | 4 | 6 | 7 | 3 | 10 | 4 | 2 | 9 |
下のヒストグラムに対応した箱ひげ図を書きなさい。
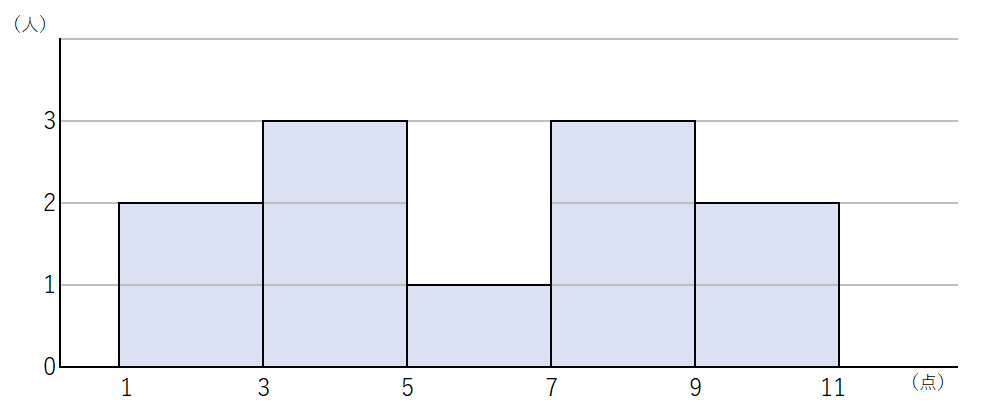
まずは、データを点数が小さい順に並べるところからスタートしよう。
1、2、3、4、4、6、7、7、8、9、10
ここから、最小値・第一四分位数・第二四分位数・第三四分位数・最大値を探そう。
最小値と最大値はすぐに見つけることができるね。
最小値 1
最大値10
次に第二四分位数(中央値)を探そう。
11人の真ん中は、6人目だね。
そうすると、第二四分位数は6ということがわかるよ。
あとは、6人目より点数が低い中での真ん中(第一四分位数)と6人目より点数が高い中での真ん中(第三四分位数)を探そう。
第一四分位数 3
第三四分位数 8
ここまで探せたら、あとは箱ひげ図は簡単に書くことができるね。
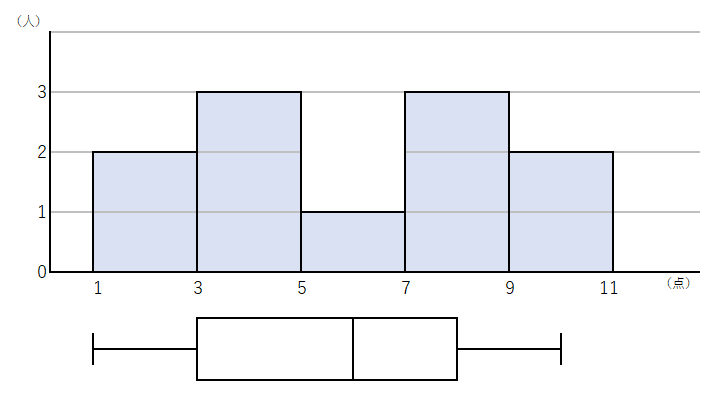
箱ひげ図とヒストグラムを比べて見てみると、それぞれの良い点がわかるよ。
ヒストグラムの良い点など
- 他の範囲との大小が比べやすい。
- おおよその平均値を求めることができる。
- ヒストグラムのデータを使って、箱ひげ図を書くことができる。
※箱ひげ図からヒストグラムを書くことはできない。
箱ひげ図の良い点など
- 第一四分位数・第二四分位数・第三四分位数・最大値・最小値がわかる。
- データの大まかな散らばり具合を予測することができる。
「箱ひげ図」と「ヒストグラム」にはそれぞれの良い点があるから、2つを組み合わせることで、それぞれの弱点を補いデータが分析しやすくなるよ。
「箱ひげ図」・「ヒストグラム」のそれぞれの特徴を理解して、データを正確に読み取れるようにしよう!
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。