四分位範囲と箱ひげ図とは?四分位数の求め方をわかりやすく解説
中学校2年生の数学で学習する「四分位範囲」と「箱ひげ図」とは何か?四分位数とはどういう意味か、どうやって求めるのかをわかりやすく図も使って解説するよ。
四分位数とは
今回は新たに変わった名前の「箱ひげ図」について勉強をしていくよ。
「箱ひげ図」の説明の前に、箱ひげ図で使われる言葉から勉強をしていこう。
まずは、「四分位数」について確認するよ。
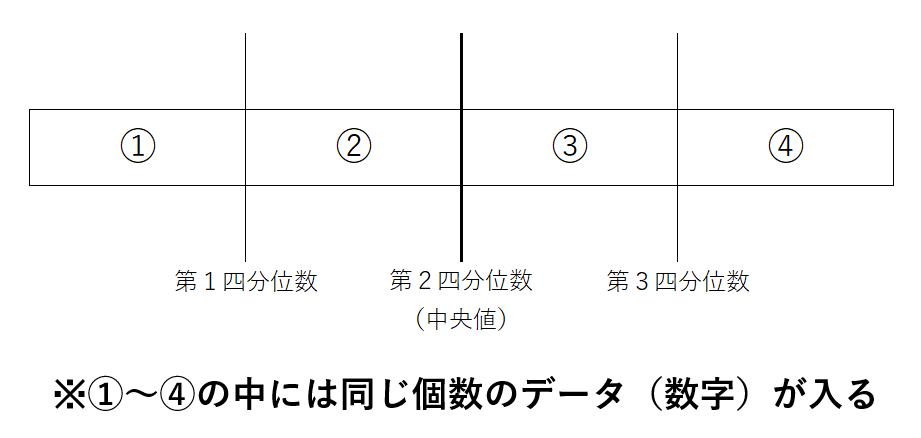
この言葉は、漢字のままの通り「四等分する位置にくる3つの区切りの数」のことなんだ。
それぞれ小さいほうから順番に
「第1四分位数」「第2四分位数」「第3四分位数」と名前がつけられているよ。
また、第2四分位数は中学1年生の時に習った「中央値」のことだよ。
早速あるクラスの数学の小テストの点数を使って、四分位数を確認してみよう。
例題
11人の数学の点数が、
17点、16点、11点、14点、15点、19点、8点、7点、9点、13点、12点だった時の四分位数を求めてみよう。
まずは、点数が低い順で並べてみると
7点、8点、9点、11点、12点、13点、14点、15点、16点、17点、19点
となるね。
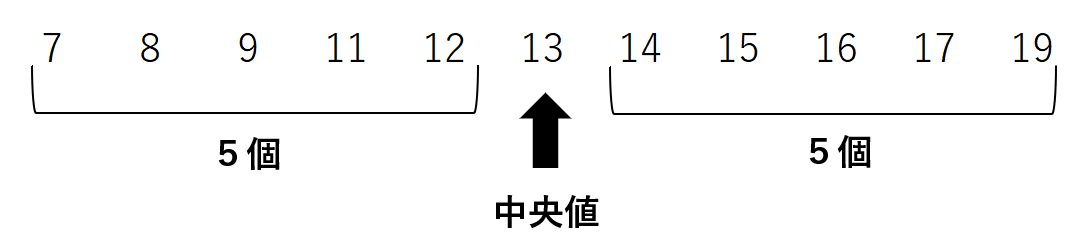
まずは、この中で真ん中の点数の「第2四分位数」を探してみよう。
11人の中で真ん中の点数は、6番目だから中央値は13点ということがわかるよ。
次に、6番目の生徒より低い点数と高い点数の中の、真ん中の点数を探してみよう。
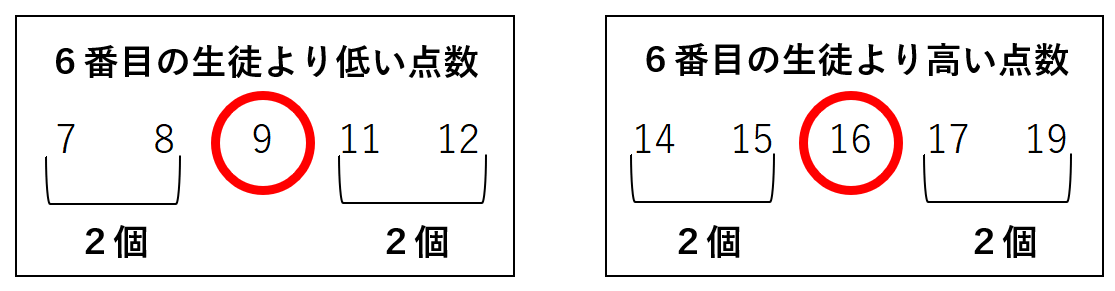
6番目より低い点数は、7点、8点、9点、11点、12点だから、真ん中の点数は9点だね。
6番目より高い点数は、14点、15点、16点、17点、19点だから、真ん中の点数は16点だね。
よって、第1四分位数は9点、第3四分位数は16点ということがわかるよ。
では次の問題の第1四分位数・第2四分位数・第3四分位数を求めてみよう。
問題
クラスの生徒8人の身長が
178cm、173cm、162cm、159cm、166cm、170cm、151cm、165cm
の時、第1四分位数・第2四分位数・第3四分位数を求めなさい。
まずは、身長が小さい順で並べてみると
151cm、159cm、162cm、165cm、166cm、170cm、173cm、178cm
となるね。
この中で、真ん中の身長を探そうとしても、きれいに4人ずつに分かれてしまって、真ん中の身長を見つけることができないよね。
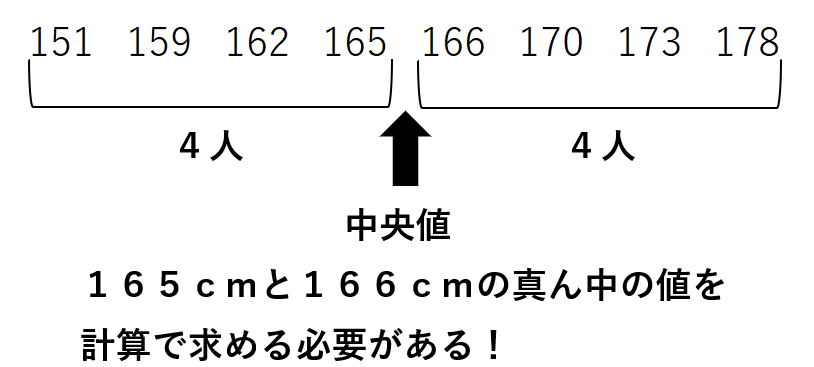
こういう場合の第2四分位数は、4番目と5番目の間の値になって、計算で求める必要があるんだ。
だから第2四分位数は、(165+166)÷2=165.5となるよ。
例題の時と同じように、1番目から4番目の真ん中の身長と5番目から8番目の真ん中の身長を探そう。
1番目から4番目の真ん中の身長と5番目から8番目の真ん中の身長のどちらも、計算で求める必要があるんだ。
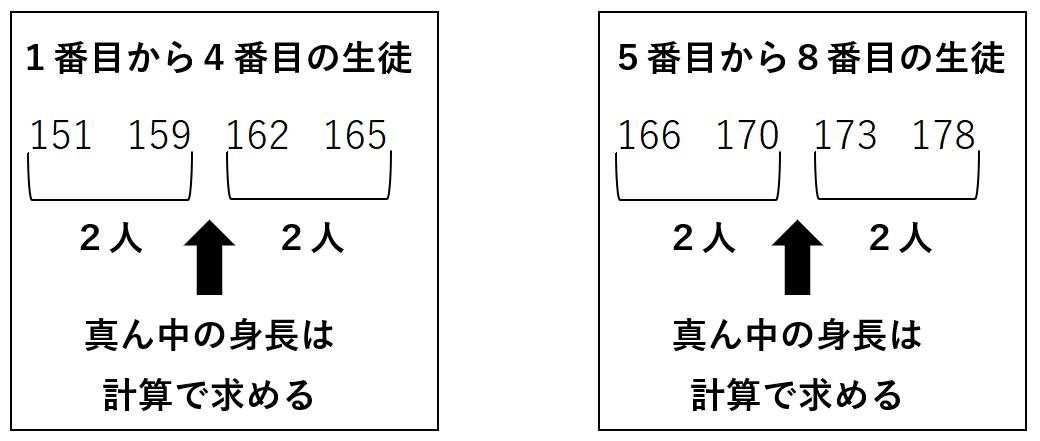
第1四分位数(1番目から4番目の真ん中の身長)(159+162)÷2=160.5
第3四分位数(5番目から8番目の真ん中の身長)(170+173)÷2=171.5
四分位数はこの問題のように、計算で求める時があるから注意しよう。
箱ひげ図とは
ここからメインの「箱ひげ図」について勉強していくよ。
面白い名前の図なんだけれど、名前の通り箱からひげが伸びた図になっているんだ。
この箱ひげ図はとても便利な図で、データの最大値・最小値・四分位数・平均値を1つの図で表しているから、データを分析する時にとてもわかりやすいんだ。
箱ひげ図について
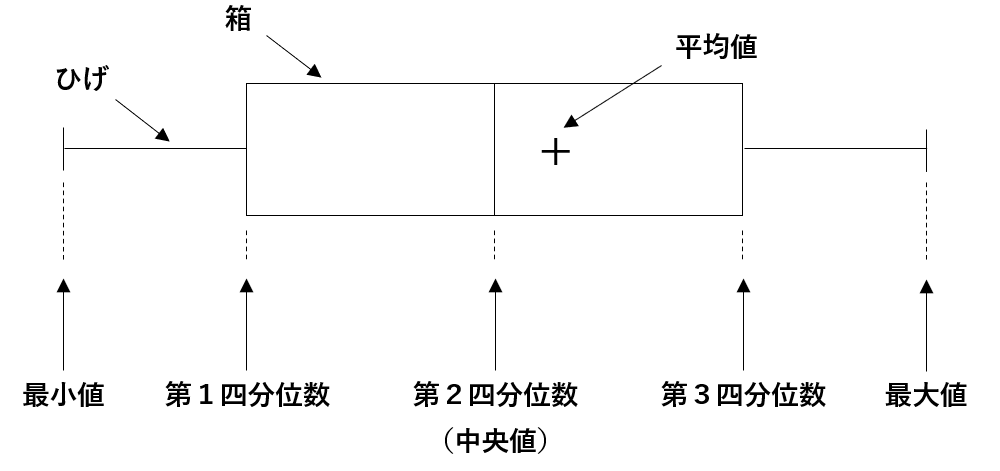
平均値は「+」のマークで書くよ。
箱ひげ図は、縦に書くこともあるよ。
上で確認した四分位数の求め方がわかれば、簡単に書くことができる図だよ。
また、入試では図を読み取る問題も出題されるから、図の各部が何を表しているか、確認していこう。
箱ひげ図で、第3四分位数から第1四分位数を引いた値を「四分位範囲」と呼ぶんだ。
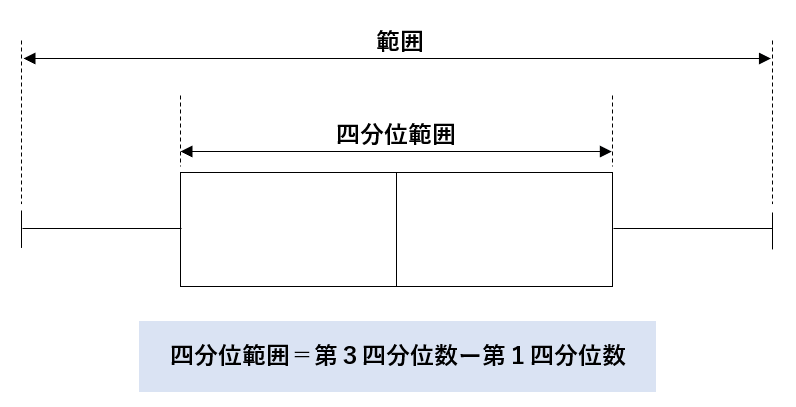
四分位範囲の値が小さければ、データのばらつきが小さくなり集中していることがわかり、四分位範囲の値が大きければ、データのばらつきが大きいということがわかるよ。
問題
クラスの生徒8人の身長が
178cm、173cm、162cm、159cm、166cm、170cm、151cm、165cm
の時、箱ひげ図を書きなさい。
(上の四分位数の問題と同じ数字を使っているよ)
箱ひげ図を書くために必要な数字を確認しよう。
最小値 151cm
第1四分位数 160.5cm
第2四分位数 165.5cm
第3四分位数 171.5cm
最大値 178cm
これを使って箱ひげ図を書くと下のようになるよ。
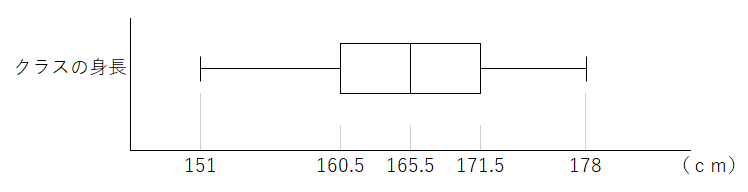
四分位数を求めることができたら、箱ひげ図は簡単に書くことができるよ。
色々な問題にチャレンジして、箱ひげ図の書き方をマスターしよう。
四分位数と箱ひげ図まとめ
・データを小さい順に並べて4等分したときの、3つの区切りの値を四分位数という。
四分位数は、小さいほうから順に、第1四分位数、第2四分位数、第3四分位数という。
・箱ひげ図は、四分位数、最大値、最小値を表したものである。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


