平行線と線分の比をわかりやすく解説(相似・平行線と比の定理)
平行線と線分の比の定理
「平行線と線分の比の定理」の単元では、
平行な線と、その平行な線に直線が交わる時にできる線分(直線上にある2つの点の間の、限られた部分のこと)の比に、ある性質があるということを学習するんだよ。
言葉で説明されても、あんまりピンとこないよね。
図で表すと、こんな感じだよ。
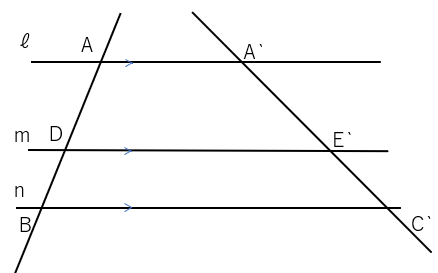
平行な線(l、m、n)に2つの直線が交わっているよね。
それによってA、D、B、A’、E’、C’という6つの交点ができているね。
このそれぞれの交点の間が「線分」だね。
こうしてできた線分の比がどんな性質を持っているのかを学習するんだね。
以前の学習では「三角形と比の定理」をやったよね?
今回やる「平行線と線分の比の定理」は「三角形と比の定理」を少しレベルアップさせた性質だと思ってもらったらOK。
なので、まずは「三角形と比の定理」の復習をしておこう。
三角形と比の定理
①DE//BCならば AD:AB=AE:AC=DE:BC
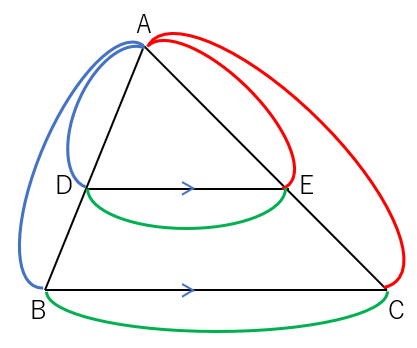
②DE//BCならば AD:DB=AE:EC
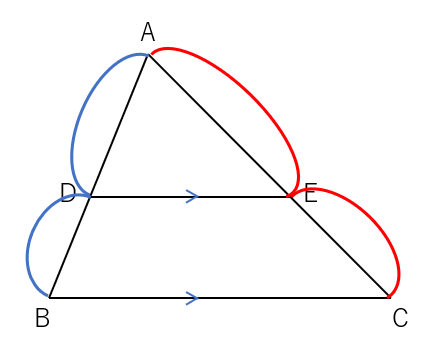
では、上の図の△ABCの「辺AC」を右に平行移動させてみるよ。
平行移動させただけだから
AC=A‘C’、AE=A’E’、EC=E’C’
になるよね。
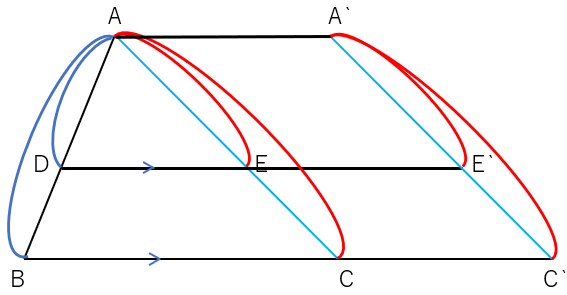
ということは、「三角形の比の定理」で確認した
AD:AB=AE:AC=DE:BC
AD:DB=AE:EC
の「AC」「AE」「EC」それぞれ
AC=A‘C’、AE=A’E’、EC=E’C’とすることができるのだから、
次のような性質が成り立つということになるんだ。
平行線と線分の比の定理

直線ℓ、m、nが平行になるとき、次の性質が成り立つ
- AD:AB=A‘E’=A’C’
- AD:DB=A’E’:E’C’
これが「平行線と線分の比の定理」だよ。
三角形と比の定理の少しレベルアップしただけだよね。
では、実際に問題にチャレンジしてみよう。
平行線と線分の比の定理の練習問題
平行線と線分の比の定理の練習問題に挑戦してみよう。
問題
直線ℓ、m、nが平行なとき、xの長さを求めなさい。
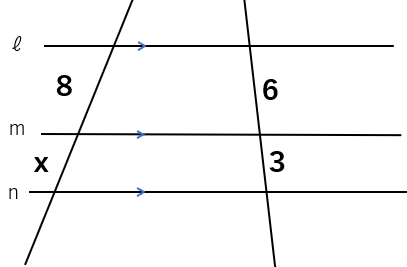
平行線と比の定理を使うと
8:x=6:3 という比例式が成り立つ。
だからこの比例式を解いて、xを求めたらいいね。
8:x=6:3 比例式の性質a:b=c:d→ad=bcを使おう
6×x=8×3
6x=24
x=4
別解
別の解き方も紹介するね。
さっきの問題を次のように考えたら、
8:(8:x)=6:(6+3)という比例式が成り立つよ。
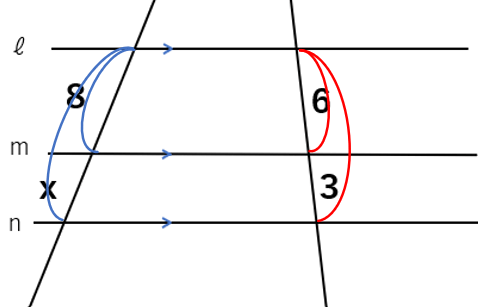
比例式を解くと
8:(8:x)=6:(6+3)
8:(8:x)=6:9 比例式の性質a:b=c:d→ad=bcを使おう
6×(8+x)=8×9 分配法則を使おう
48+6x=72
6x=72-48
6x=24
x=4
この方法だとすこし計算が面倒になるね。
平行線と線分の比の定理は2つあるけれど、どっちを使うかは問題によって使い分けよう。
直線ℓ、m、nが平行なとき、xの長さを求めなさい。
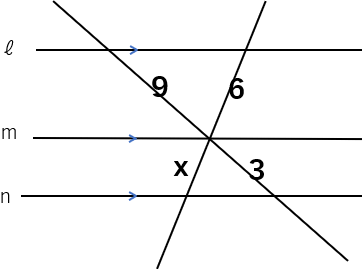
この問題のパターンは、形から「砂時計形」と呼ばれることもあるらしいよ。
この図を見ると、「あれ?平行線と比の性質が使えない気がするな」と思った人もいるかもしれないね。
ただ、次のように直線を平行移動してみよう。
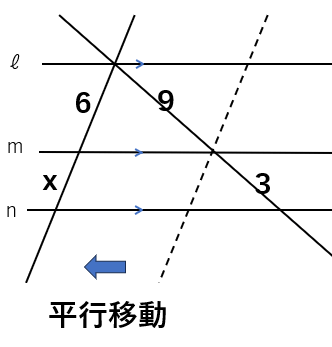
見慣れた形になったね。
ちなみに、この形を「ピラミッド型」と呼ぶこともあるらしいよ。
平行移動したということは、それぞれの長さは変わらないから、次のような比例式が成り立つよ。
6:x=9:3
9x=18
x=2
「平行線と線分の比の定理」まとめ
平行線と線分の比の定理

直線ℓ、m、nが平行になるとき、次の性質が成り立つ
- AD:AB=A‘E’=A’C’
- AD:DB=A’E’:E’C’
※どちらの性質を使うかは問題によって使い分けよう。
「定理を使えないな」と思っても、どちらかの直線を平行移動すると、定理が使えるようになることがあるので、よく考えてみることが大事だよ。
※問題をたくさん解いて、いろいろな問題パターンに触れておくのがおすすめ!
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。


