「yはxの二乗に比例する関数の利用」頻出・応用問題の解き方
中学校3年生の数学で学習する「いろいろな関数の利用」について、「yはxの二乗に比例する関数の利用」の定期テストでよく出る問題のパターンや、応用問題の解き方をくわしく解説するよ。
振り子の問題・図形の面積を求める問題、料金を求める問題など、いろいろなパターンの問題の解き方を確認しよう!
振り子の問題
「振り子」ってわかるかな?「振り子時計」や「理科の実験」で見たことがある人もいるんじゃないかな?
実は、振り子の動きは「二乗に比例する関数」にものすごく関係しているんだ。
振り子が、行って帰ってくるまでの時間のことを「周期」と呼ぶよ。
周期と関係しているものは振り子の長さなんだ。
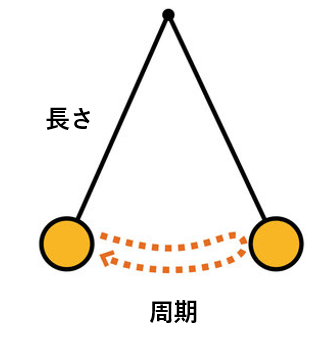
振り子の周期x秒と長さymの関係
y=\(\frac{1}{4}\)x2
で表される。
y=ax2の形になっているから、「二乗に比例する関数」といえるよね。
上の式から周期xが長いほど、振り子の長さが長くなることがわかるかな。
ただ、想像してみたら当たり前のことだよね。下図の振り子で周期が短いのはどちらかと聞かれたら、長さが短い左側になるね。
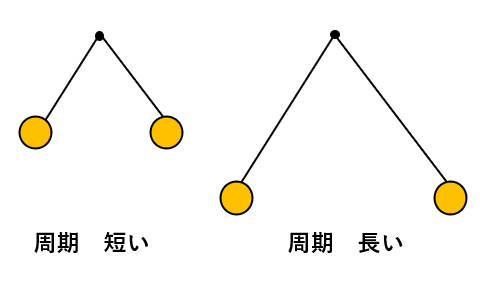
振り子の長さを求める問題
例題
振り子の周期がx秒で、振り子の長さがymの振り子にはy=\(\frac{1}{4}\)x2という関係がある。
周期が6秒だった時、振り子の長さを求めなさい。
周期が6秒ということは、x=6ってことだよね。だから、x=6をy=\(\frac{1}{4}\)x2に代入するよ。
y=\(\frac{1}{4}\)x2
y=\(\frac{1}{4}\)×62
y=\(\frac{1}{4}\)×36
y=9
振り子の長さは9mと求めることができるね。
ハイジのブランコの長さを求める
アルプスの少女ハイジって知っているかな?スイスで作られた話なんだけど、日本でも放送されていたんだよ。
10年前にはCMにも登場していたんだ。そのCMでは、ハイジという少女がブランコに乗っているんだけれど、そのブランコの長さがあまりにも長すぎると話題にもなったんだ。

今でもユーチューブで「ハイジ ブランコ」と調べたらブランコの映像が出てくるから、気になる人は動画を観てみて、周期を測ってみてね!!
動画で確認してみると、なんと周期は10秒もあるよ。
ということは、
x=10をy=\(\frac{1}{4}\)x2に代入するよ。
y=\(\frac{1}{4}\)x2
y=\(\frac{1}{4}\)×102
y=\(\frac{1}{4}\)×100
y=25
ハイジが乗っているブランコの長さは25mということがわかるね。
25mというと、マンションの7~8階の高さと同じくらいになるよ。
25mの長さのブランコを笑顔で乗っているハイジはすごい勇者だと言えるね。
面積を求める問題
例題
下の図のように、直角二等辺三角形ABCと正方形DEFGが並んでいる。
正方形を固定し、直角二等辺三角形ABCを矢印の方向に秒速2cmで点Cが点Fに重なるまで動かす。
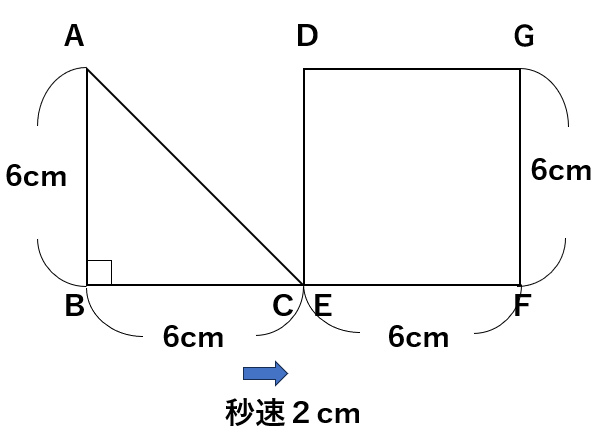
(1)1秒後に、直角二等辺三角形と正方形が重なってできる部分の面積を求めなさい。
(2)x秒後に、重なってできる部分の面積をycm2とすると、yをxの式で表しなさい。
(1)1秒後の直角二等辺三角形と正方形が重なってできる部分の面積の求め方
1秒後には2×1=2cm進むから、次のようになっているよ。
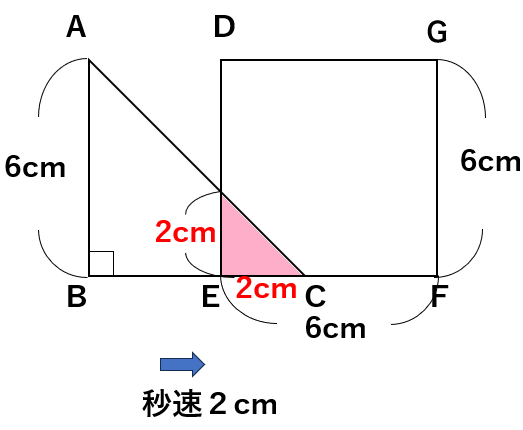
ここで大事なことは、重なる部分(ピンク色)が直角二等辺三角形になるということ。
つまり、2辺の長さが等しくなるから、2辺が2cmになるよ。
疑問に思ったら読もう!
なぜ重なる部分が直角二等辺三角形になるの?
辺ACと辺DEの交点をHとするよ。
➀三角形ABCは、直角二等辺三角形なので、∠A=∠Cだね。
➁∠B=∠E=90°なので、辺ABと辺DEは平行だね。
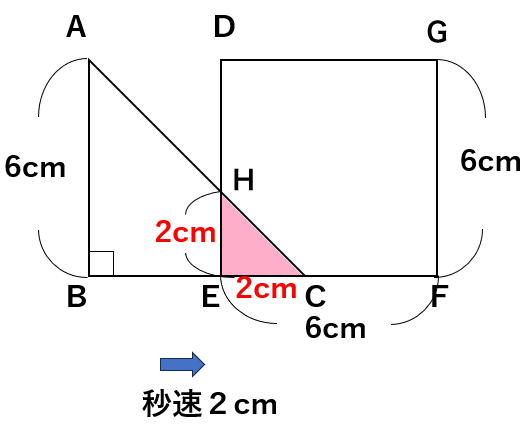
④∠EHCは、∠Aと同位角なので、➀より、∠EHC=∠Cだね。
2角が等しいので、三角形EHCは、二等辺三角形となるよ。
なので、辺EH=辺ECとなるんだね。
2つの図形が重なっている部分は、1辺が2cmの直角二等辺三角形になって、
面積は(底辺)×(高さ)÷2だから
2×2÷2=2cm2
と求められるね。
(2)x秒後に、重なってできる部分の面積をycm2としたとき、yをxの式で表す
x秒後には2×x=2xcm進むから、次のようになっているよ。
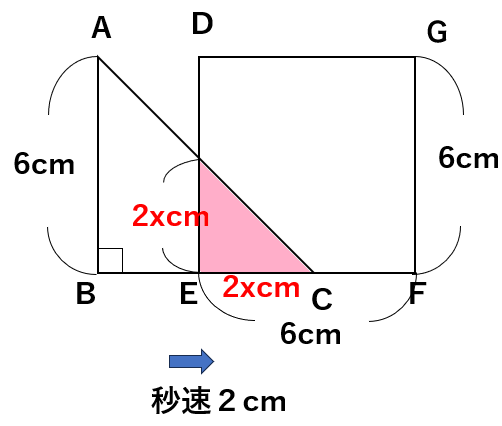
2つの図形が重なっている部分は、1辺が2xcmの直角二等辺三角形になって、
面積yは(底辺)×(高さ)÷2だから
y=2x×2x÷2=2x2cm2
と求められるね。
y=2x2という式で表されるから、これも「二乗に比例する関数」といえるね。
制動距離の問題
「制動距離」という言葉は、車の運転をしたことがないと、あまり聞かないかもしれないね。
制動距離とは、車を走らせていたとき、ブレーキをかけてから、実際に車が完全に止まるまでの距離のことなんだ。
「車は急に止まれない」と言うよね。
例えば、みんなはゆっくり歩いているとき、急に止まろうと思えば、ピタっと急に止まったりできるよね。
でも、もし全力疾走で走っていたらどうかな?
急にピタッと止まろうとしても、前につんのめって倒れそうにならないかな?
これは、「運動をしている物体は、外から力を加えないかぎり、そのまま運動を続けようとする力(慣性の法則)」がはたらくからなんだ。
スピードを出している車も同じで、運動を続けようとする力がはたらくのを、タイヤと地面の摩擦抵抗で止めようとするんだよ。
そうやって「車が完全に止まる」までにかかる時間によって、車が進んでしまう距離が「制動距離」なんだね。
このは制動距離は、速さの二乗に比例するんだ。
つまり速ければ速いほど、止まるまでの距離が長くなるってことだよ。なんとなくイメージできるよね。
時速100kmの車と、時速10kmの車では止まるまでの距離が全く違うからね。
速さと制動距離の関係
例題
時速60kmの車の制動距離は27kmである。
このとき時速xkmの制動距離がykmとして、yをxの式で表しなさい。
制動距離yは、速さxの二乗に比例するから、y=ax2という式になるよ。
aの値を求めるために、x=時速60kmとy=27kmを代入してみよう。
y=ax2
27=a×602
27=a×3600
27=3600a
a=\(\frac{27}{3600}\)
a=\(\frac{3}{400}\)
aの値が求まったから、もとの式に代入して
y=\(\frac{3}{400}\)x2
という式になるね。
時速100kmの制動距離
例題
y=\(\frac{3}{400}\)x2を使って、時速100kmの制動距離を求めなさい。
制動距離はxだから、x=100をy=\(\frac{3}{400}\)x2に代入してみよう。
y=\(\frac{3}{400}\)x2
y=\(\frac{3}{400}\)×1002
y=\(\frac{3}{400}\)×10000
y=75
時速100kmの制動距離が75mと求めったね。つまり、ブレーキをかけてから止まるまでに75mは車が進むってことだね。
次に時速10kmの制動距離を求めてみよう。
時速10kmの制動距離
例題
y=\(\frac{3}{400}\)x2を使って、時速10kmの制動距離を求めなさい。
制動距離はxだから、x=10をy=\(\frac{3}{400}\)x2に代入してみよう。
y=\(\frac{3}{400}\)x2
y=\(\frac{3}{400}\)×102
y=\(\frac{3}{400}\)×100
y=0.75
時速10kmの制動距離は0.75mと求められたね。つまり、ブレーキをかけてから止まるまでに0.75mは車が進むってことだね。ただ、0.75mって75cmだから本当にわずかだよね。
時速10kmと時速100kmの制動距離の違い
時速10kmと時速100kmのときの制動距離をまとめると次のようになるよ。
| 時速10km | 時速100km |
| 制動距離は0.75m | 制動距離は75m |
速さは10倍になっているけど、制動距離は100倍になっているよね。つまり、制動距離は速さの二乗に比例するってこと。
だから車の運転では、あまり速いスピードを出してはいけないということなんだね。
空走距離
免許を取るときにも大事になってくるんだけど、制動距離以外に、もう一つ大事な距離があるんだ。
それは「空走距離」。
今はまだ、運転しているのは基本的に人間だよね。
人間は、「危ないっ!」と思っても、実際に手足が動くまでには、すこし時間がかかってしまうんだ。
空走距離というのは、「危ないっ」と思ってからブレーキを踏むまでの時間で進んでしまう距離のことで、これは速さに比例することが知られているよ。
だから実際は
車の停止距離=空走距離+制動距離
と表すことができるよ。
料金を求める問題
「いろいろな関数の利用」では、「二乗に比例する関数」ではないものについても問題に出ることがあるよ。
ここでは、すこし変わった関数についての問題を紹介するよ。
例題
荷物の送料は次のようになっている。
| 重さ | 2kgまで | 5kgまで | 7kgまで | 9kgまで | 10kgまで |
| 料金 | 300円 | 600円 | 800円 | 900円 | 1000円 |
このとき、重さをxkg、そのときの料金をy円としてグラフを書きなさい。
送料を見ると、次のように思う人もいるんじゃないかな?
- 比例でもないな
- 反比例でもないな
- 一次関数でもないな
- 二乗に比例する関数でもないな
→どうやってグラフを描いたらいいんだろう!?
じつは、これは今までやったことがないグラフになるんだ。
順番に説明していくね。
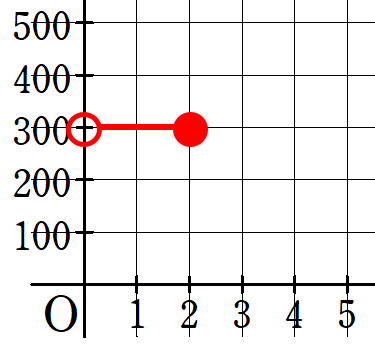
まず、2kgまでは300円だから、グラフは次のようになるよ。
2つポイントがあるよ。
ポイント
- 0kgのときは0円だよね。
0kgなのに、料金が300円かかったらびっくりしちゃうよね。
だから、「0kgのときは300円にはならないよ」という意味で「〇」になっているよ。
- 「2kgまでは300円」だから、2kgのときは300円になるよね。
だから、「2kgのときは300円になるよよ」という意味で「●」になっているよ。
- 「〇」は「入らない」。「●」は「入る」と覚えておこう。
次に、5kgまでは600円だから、グラフは次のようになるよ。
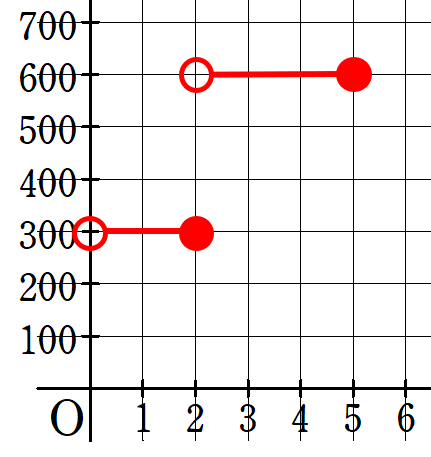
間違えやすいところは、「2kgのとき」。
2kgのときは300円で、600円にはならないから「〇」になっているよ。
こんな感じでグラフを作っていこう。
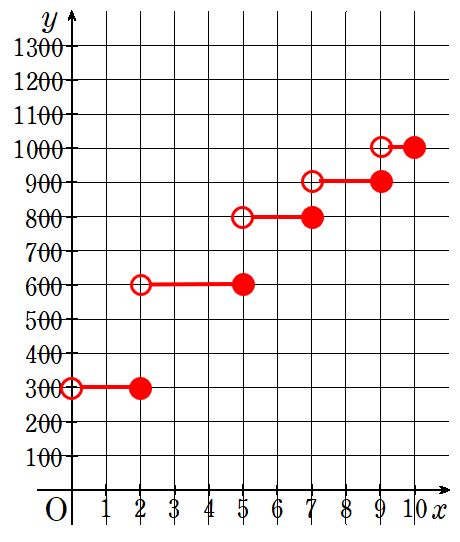
新しい形のグラフだよね。このように階段になっているグラフのことを「階段関数」というよ。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。



詳しく載ってていいね!