「式の計算の利用」文字式・乗法公式を使って工夫と証明をしよう
中学校3年生の数学で学習する「式の計算の利用」について、「文字式を利用して計算を工夫する方法」「乗法公式を使って数の性質を証明する方法」「文字式を利用して図形の性質を証明する方法」をそれぞれわかりやすく解説するよ。
これまでの学習で、文字を使った式を考えたり、乗法公式を使って多項式×多項式を展開させることができるようになったね。
文字式や乗法公式を利用すると、普通に計算すると大変そうな式を簡単に計算したり、数の性質を証明をしたり、図形の性質を証明したりすることができるんだ。
ここでは、
➀文字式と乗法公式を使って複雑な計算を工夫する方法
➁乗法公式を使って数の性質を証明する方法
③文字式を利用して図形の性質を証明する方法
この3つをくわしく紹介するよ。
102×98を乗法公式を使って計算してみよう
102×98の計算って普通はひっ算を使ってやるよね。
ただ、乗法公式を使うとすぐに答えを求められるんだよ。
次の乗法公式を思い出してみよう。
乗法公式
(x+a)(x-a)=x2-a2
この公式を使うために、102と98を次のように考えてみるんだ。
- 102=100+2
- 98=100-2
そうすると、
102×98=(100+2)×(100-2)
と表すことができるよね。(ただ「×(かける)」は省略するよ。)
(100+2)(100-2)って、乗法公式の「(x+a)(x-a)=x2-a2」と同じ形だということに気が付くかな?
そう、だから乗法公式が使えるようになるんだ。
(100+2)(100-2)を展開すると、「前(100)の2乗」-「後ろ(2)の2乗」の形になるから、
1002-22
=10000-4
=9996
と求めることができるよ。乗法公式を使えば、「102×98」なんていう大変そうな計算でも暗算で答えられそうだね。
ポイント
乗法公式「(x+a)(x-a)=x2-a2」を使うために、102×98を(100+2)(100-2)のように、(前+後)(前-後)みたいな形にしているよ。
このように、式をちょっと形を変えて工夫したら、乗法公式が使えるようにならないかを考えてみるのがポイントだよ。
数の性質を乗法公式を使って証明してみよう
「数の性質を使った証明」は1年生や2年生でも学習したよね。例えばこんな問題をやったはず!
- 2つの続いた整数の和は奇数になる。
- 2桁の自然数と、十の位と一の位を入れ替えた数の和が11の倍数になる。
1、2年生と3年生の証明の仕方の違いは「乗法公式を使う」というところだよ。
実際に問題を紹介するね。
3年生で登場する「数の性質の証明」の例題
- 2つの続いた奇数の積に1を足した数は4の倍数になる。
- 2つの続いた整数で、大きい方の2乗から小さい方の2乗を引いた差が奇数になる。
それではそれぞれの例題をどうやって乗法公式を使って証明するのか、説明していくよ。
「2つの続いた奇数の積に1を足した数は4の倍数になる」証明
「2つの続いた奇数」というと、「1、3」「3、5」「5、7」みたいな組み合わせのことだよね。
2つの続いた奇数の積に1を加えると本当に4の倍数になるのか計算してみよう。
2つの続いた奇数の積
1×3 +1 =4
3×5 +1 =16
5×7 +1 =36
確かに4の倍数になっていることがわかるね。
ただ、これじゃあ、3パターンでしか証明できたことにはならないんだ。
すべての数字で確かめるのは大変だから、「文字」を使って証明するよ。
「文字」を使って証明できたら、すべての数字で証明できたことになるんだよ。
実際にやってみよう。
2つの続いた奇数を文字で表そう。
「1、3」「3、5」みたいな「2つの続いた奇数」を文字を使って表すと、「2n-1、2n+1」や「2n+1、2n+3」のように表すことができるよ。
なぜかというと
整数をnとすると、偶数って2の倍数のことだから「2n」と表せるよね。
偶数が2nになる理由を忘れてしまっていたら確認しよう!
2=2×1
4=2×2
6=2×3
すべて偶数は、2×(整数)と表すことができるよね。
(整数)=nとすると、2×n=2nになるよ。
奇数は
- 偶数(2n)-1 (偶数から1引いたら奇数)
- 偶数(2n)+1 (偶数に1足したら奇数)
だから、「2n-1」や「2n+1」と表せるんだよ。
もしくは、「2n+1」、「2n+3」と表してもいいよ。
2つの続いた奇数の積に1を加えた数が4の倍数になる証明
2つの続いた奇数は2n-1、2n+1と表すことにするよ。
2つの積は(2n-1)(2n+1)になるよね。
これに1を加えると次のようになるよ。
(2n-1)(2n+1)+1
「(2n-1)(2n+1)」は「(前+後)(前-後)」の形になっているから、次の乗法公式が使えるよ。
乗法公式
(x+a)(x-a)=x2-a2
乗法公式を使って「(2n-1)(2n+1)」を展開して1を加えてみよう。
(2n-1)(2n+1)+1
=4n2-1+1
=4n2
ここで、nは整数だったから、n2も整数になるよね。
(だって、整数を2乗したら、答えも整数になるに決まっているよね。小数や分数になるわけがないよね。)
n2が整数なんだから、4n2は4×(整数)になるよね。4×(整数)ということは、4の倍数になることと同じだから、
「2つの続いた奇数の積に1を加えた数が4の倍数になる」というわけなんだよ。
最後にまとめてみよう。
整数をnとすると、2つの続いた奇数は2n-1、2n+1と表せる。
2つの続いた奇数に1を加えた数は
(2n-1)(2n+1)+1
=4n2-1+1
=4n2
n2は整数なので、4n2は4の倍数になる。よって、「2つの続いた奇数の積に1を加えた数は4の倍数になる」。
「2つの続いた整数で、大きい方の2乗から小さい方の2乗を引いた差が奇数になる」証明
「2つの続いた整数」というと、「1、2」「2、3」「3、4」みたいな組み合わせのことだね。
2つの続いた整数で、大きい方の2乗から小さい方の2乗を引いた差が奇数になるか計算してみよう。
| 大きい方の2乗 | 小さい方の2乗 | 差 |
| 22 | 12 | 22-12=4-1=3 |
| 32 | 22 | 32-22=9-4=5 |
| 42 | 32 | 42-32=16-9=7 |
確かに奇数になっていることがわかるね。
ただ、これじゃあ、3パターンでしか証明できたことになはらないね。
すべての数字で確かめるのは大変だから、同じく「文字」を使って証明するよ。
2つの続いた整数を文字で表そう。
「1、2」「2、3」みたいな「2つの続いた整数」を文字で使って表すと「n、n+1」や「n+1、n+2」のように表すことができるよ。
2つの続いた整数で、大きい方の2乗から小さい方の2乗を引いた差が奇数になる証明
2つの続いた整数を「n」、「n+1」と表そう。
- 大きい方の2乗は「(n+1)2」
- 小さい方の2乗は「n2」
になるよね。下の乗法公式を使って(n+1)2を展開して、2つの数の差を計算してみよう。
乗法公式
(x+a)2=x2+2ax+a2
大きい方の2乗-小さい方の2乗
=(n+1)2-n2 ←乗法公式を使って展開しよう。
=n2+2n+1-n2
=2n+1
「2n+1」ってなったら奇数だったよね。
だから、2つの続いた整数で、大きい方の2乗から小さい方の2乗を引いた差は奇数になるんだよ。
最後にまとめてみよう。
整数をnとすると、2つの続いた整数はn、n+1と表せる。
大きい方の2乗から小さい方の2乗を引いた差は
(n+1)2-n2
=n2-2n+1-n2
=2n+1
nは整数なので、2n+1は奇数になる。よって、「2つの続いた整数で、大きい方の2乗から小さい方の2乗を引いた差は奇数になる」。
文字を使った式を利用して図形の性質を証明してみよう
それでは今度は、文字式を利用して図形の性質(その図形がどんな性質をもっているのか)を証明してみるよ。
直線の道の面積を求める計算式
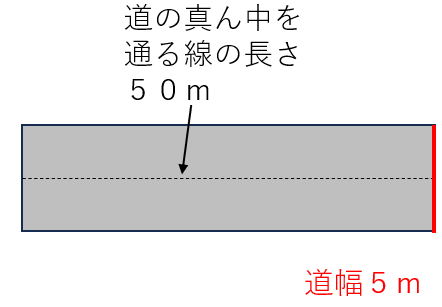
上のような道があったとすると、灰色の道の面積は、
道幅×道の真ん中を通る線の長さ
=5×50
=250m
と求められるよね。
ここまでは当たり前のことで、イメージしやすいと思う。
じゃあ次の場合はどうだろうか?
円の道の面積を求める計算式
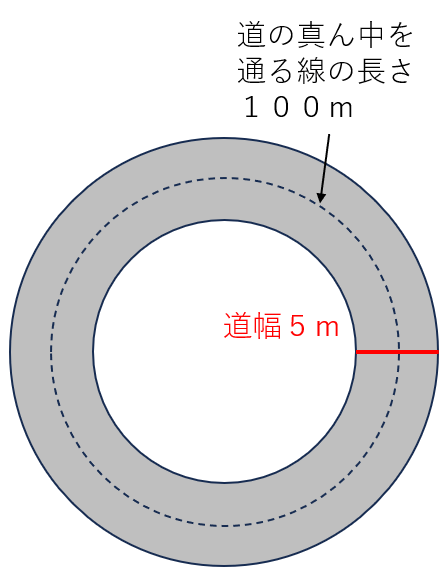
上の図のような道があったとすると、灰色の道の面積どうなるだろうか?
なんだかとても難しそうだよね。
でも、実はさっきと同じような計算の式で求められるんだ!
だから、答えは
道幅×道の真ん中を通る線の長さ
=5×100
=500m2
となるんだよ。
でも、円の道の面積が、さっきの直線の道の面積と同じような計算の式で求められるなんて、なんだか不思議だよね。
そこで、今回は次のことを証明しよう。
円の場合でも、
道の面積S=道幅a×道の真ん中を通る線の長さℓ
になる。
数式で書くと、S=aℓ。
道の面積=道幅×道の真ん中を通る線の長さになる理由
半径r mの土地の周りにできる道を考えよう。道の面積をS、道幅をa m、道の真ん中を通る線の長さをℓ mとするよ。
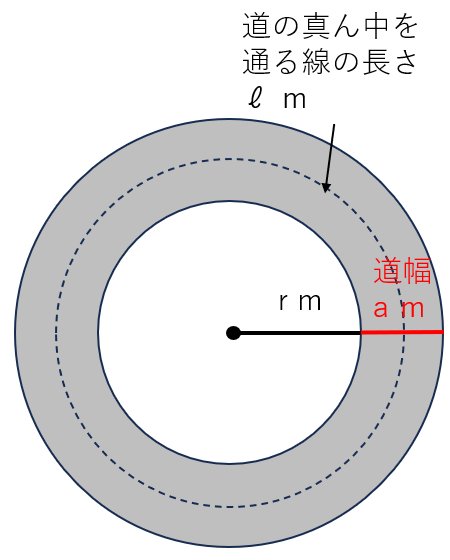
道の面積を求めるためには、大きい円から小さい円を引けばいいよね。
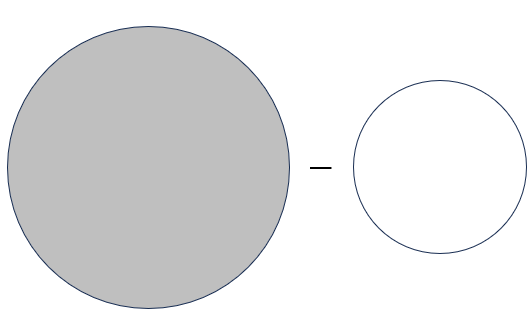
まず大きい円の面積を求めよう。
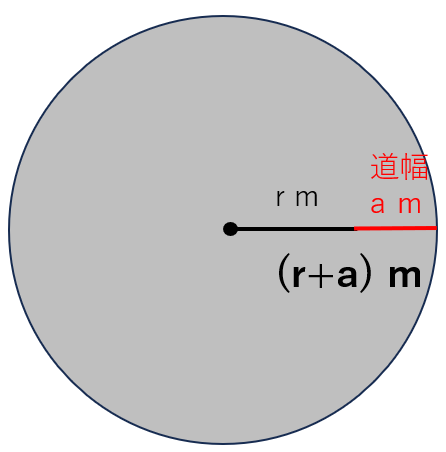
半径は(r+a)mだから、円の面積は
半径×半径×円周率
=(r+a)2×π
になるよ。ここで乗法公式を使って(r+a)2を展開して計算してみよう。
(r+a)2×π
=(r2+2ar+a2)×π
=πr2+2πar+πa2
大きい円の面積は(πr2+2πar+πa2)m2と求めることができたね。
次は小さい円の面積を求めよう。
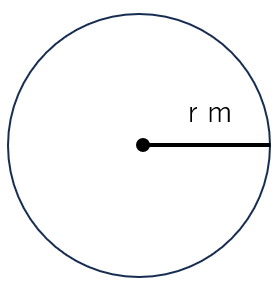
小さい円の面積は、半径r mだから、
半径×半径×π
=r×r×π
=πr2
最後に大きい円の面積から小さい円の面積を引いてみよう。
(πr2+2πar+πa2)-πr2
=2πar+πa2
下の図の灰色の道の面積Sが(2πar+πa2)m2になることがわかったね。

やっと、道の面積Sが求められたんだけど、実はこれで終わりじゃないんだよ。今回証明したいことは次のことだったよね。
円の場合でも、
道の面積S=道幅a×道の真ん中を通る線の長さℓ
になる。
下の図形で、道の真ん中を通る線の長さℓをaやrを使って表そう。
赤色で示した「道の真ん中を通る線の長さℓ」は「半径(r+\(\frac{a}{2}\))の円周」のことだよね。
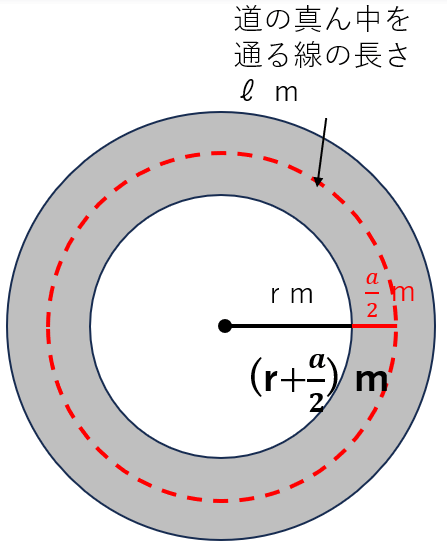
半径(r+\(\frac{a}{2}\))の円周は 直径×円周率で求められるよ。
直径×円周率
=(r+\(\frac{a}{2}\))×2×π ←半径を2倍したら直径だから「×2」
=(r+\(\frac{a}{2}\))×2π ←分配法則でかっこをはずそう
=r×2π+\(\frac{a}{2}\)×2π
=2πr+πa
道の真ん中を通る線の長さℓは
ℓ=2πr+πa
となることがわかったね。
ここまでのまとめ
灰色の道の面積 S=2πar+πa2
道の真ん中を通る線の長さ ℓ=2πr+πa
2つの式を見比べてみると、すごく似ているよね。
ということは、あともうひと踏ん張り!
「2πar+πa2」は「2πr+πa」に「a」がかけられていることがわかるかな?
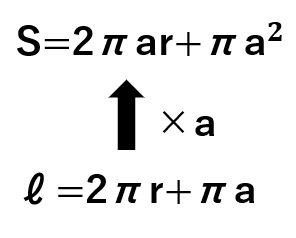
だから、S=ℓ×aになって、
S=aℓになるんだよ。
Sは道の面積、aは道幅、ℓは道の真ん中の線の長さだったので、次のことが証明できたよ。
円の場合でも、
道の面積=道幅×道の真ん中を通る線の長さ
になる。
式の計算の利用 まとめ
「式の計算の利用」では、今まで学習した「文字式」や「乗法公式」を使って、複雑な計算を簡単にしたり、数の性質を証明したり、図形の性質を証明したりできるように学習をしたね。
式が複雑になってくると、「難しい!」と拒否反応が出てくるひともいるかもしれない。
ポイントは、「謎解き」感覚で、どうやったら文字式であらわすことができるか?どうやったら乗法公式の形にできるか?を考えることだよ。
問題として出されているんだから、かならず文字式や乗法公式の形にすることができるはずなんだ。
問題の「整数」とか「奇数」とか、「倍数」という言葉から文字式がスムーズに思い浮かぶように、たくさん問題を解くのも大切だよ。だいたいパターンが決まってくるからね。
あとは、問題文の言葉どおりにそれぞれの文字式の関係を表していって、乗法公式の形がどこかに隠れていないか探してみよう。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


