ある点から円への接線の作図の書き方をわかりやすく解説
中学3年生の数学で学習する「円への接線」について、ある点から円への接線の作図の書き方をわかりやすく解説しているよ。円への接線と円周角の定理の関係、円外の1点から、その円にひいた2つの接線の長さがなぜ等しくなるのかを説明しているよ。
ある点から円への接線を作図してみよう
これまで、円周角の定理を学習してきたけれど、「今度はいきなり接線?」と思った人もいるかもしれないね。
実は「円周角の定理」と「接線」には深い関係があるんだよ。
なんと「円周角の定理の逆」を知っていると、円への接線を簡単に書くことができるんだ。
まず、中1で勉強した接線の復習をしていこう。
円への接線とは
「接線」とは、円と1点で接する直線 のことだよ。
たとえば、下の図の赤い直線のように、「円の表面?にピッタリとくっついている」ような直線だね。
もしもこの直線がもっと下(円の内側)にあったら、円と直線は2点で交わってしまうし、逆に上(円のもっと外側)にあったら、円と直線は交わらなくなってしまうよね。
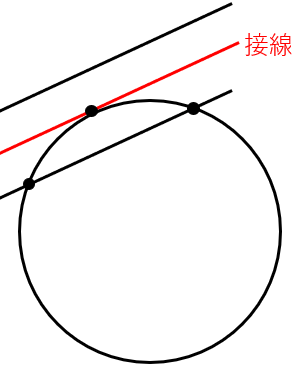
だから「接線」は、「1点で交わる」というのがポイントだよ。
この1点のことを「接点」と呼んだよね。
円への接線の性質
円への接線は、接する円の半径と垂直に交わるという性質があるよ。
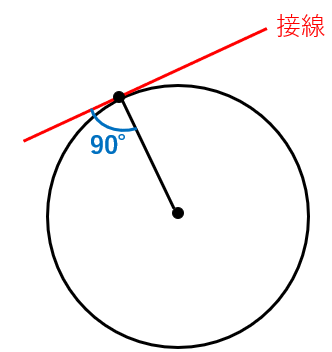
円への接線とは
円と1点(接点)で接する直線のこと
円への接線の性質
円の半径と接線は垂直に交わる
ある点から円への接線を作図する方法
点Aから円Oへの接線を引いてみよう。
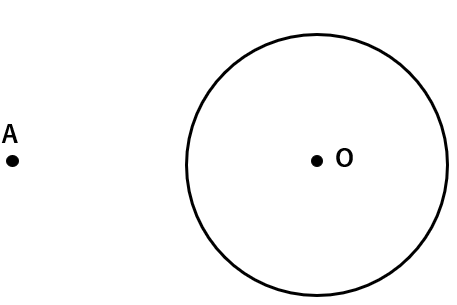
なんとなく「円にピッタリ接していそうな直線」を感覚でも描けそうな気がするけど、もちろんそれでは正確な接線とは言えないよね。
拡大してみると、2点で交わっているかもしれないからね。
それでは、正確に書く方法を紹介するよ。
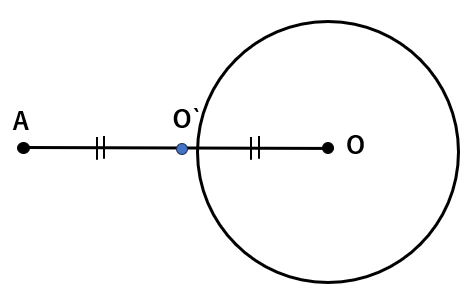
STEP1 点Aと中心Oを結ぼう
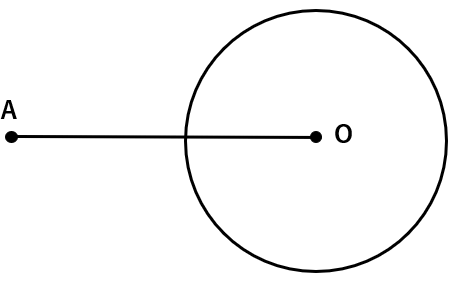
STEP2 AOの垂直二等分線を描いて、AOの中点O’を見つけよう
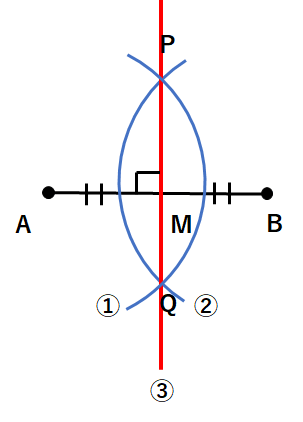
※垂直二等分線の描き方がわからない人は下を見て復習しよう。
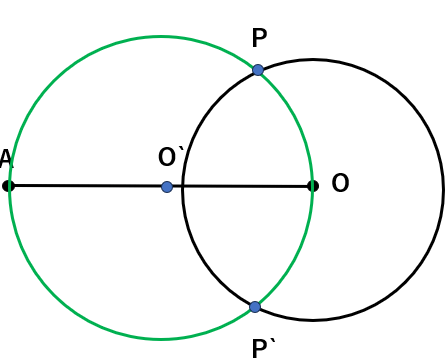
STEP3 円の中心O’からAまでを半径とした円を描く(円OとO‘が交わったところをP、P‘とする)
STEP4 点AとP、点AとQを結べば、円への接線が完成する
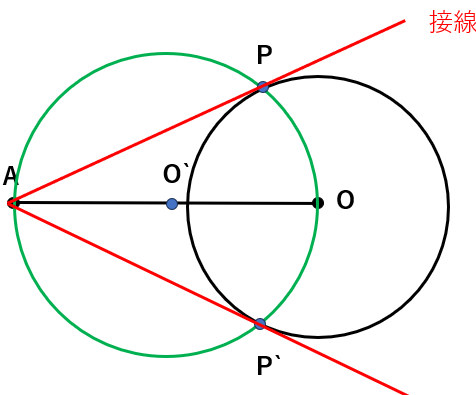
円への接線の作図ができる理由
どうしてこの方法で、円への接線が作図できるのだろう?
まずは、上の図で、赤線が本当に円Oの接線になっているのかを確かめよう。
接線は、半径と90°で交わるという特徴があったよね。
だから、赤線と半径を結んだ線が90°になることがわかったら、赤線は接線だと言えるよね。
OPを結んでできる角、∠APOと、直径AOに注目してみよう。
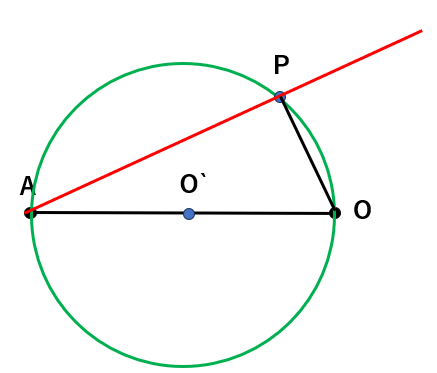
直径と円周角の定理を使うと∠APOは90°になるよね。
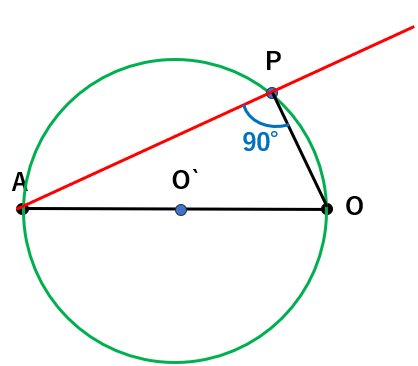
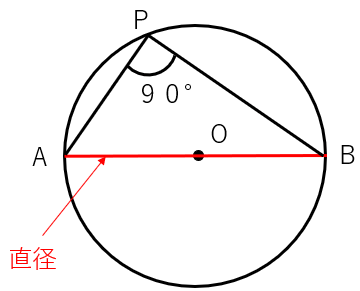
直径と円周角の定理
線分ABを直径とする円の円周上に点Pを取ると、∠APB=90°になる
∠APO=90°になるということは、円Oの半径と赤線は90°で交わるということだよね。
だから赤線は円Oの接線だと言えるんだよ。
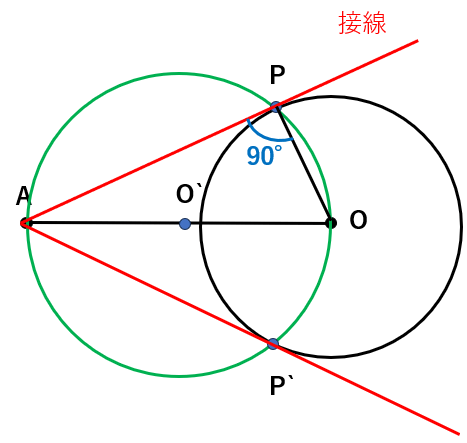
円外の1点から、その円にひいた2つの接線の長さ
円への接線の性質で大切なものを紹介するね。
円と接線の性質
円外の1点から、その円に引いた2つの接線の長さは等しくなる
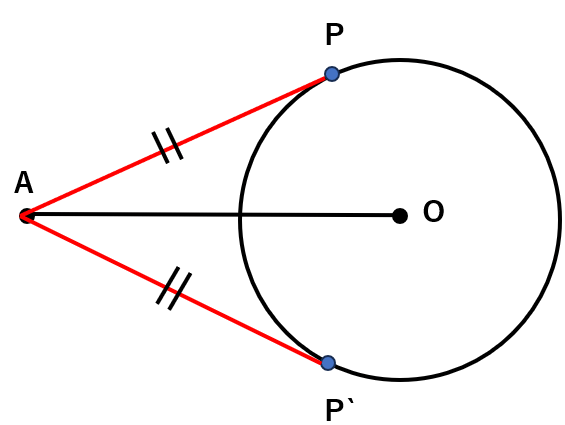
つまり、AP=AP’になるということだよ。
なぜAPとAP’が等しくなるのかを考えてみよう。
まず点Oと、PとP’それぞれを結ぶ直線(半径OP、OP’)を引こう。
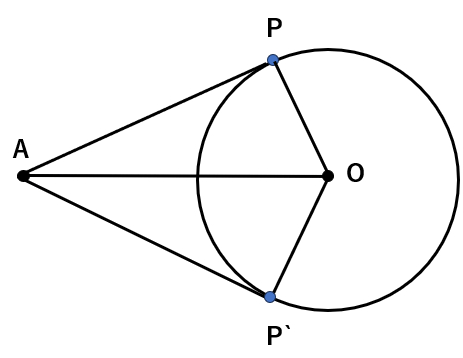
そうすると出来上がる2つの三角形、△AOPと△AOP’は合同になるんだ。
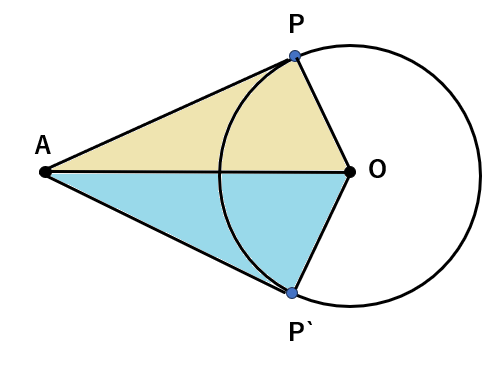
合同になる理由
⓵AOは共通(重なっているよね)
②半径だからOPとOP‘は等しいよね。
③接線と半径は90°で交わるよね
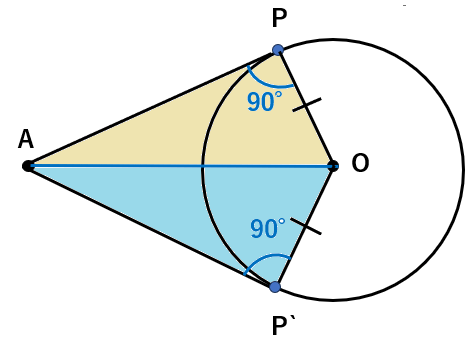
①②③から、直角三角形の斜辺と他の1辺がそれぞれ等しいから
△AOP≡△AOP’
合同だということは、2つの三角形はぴったりと重なるということだよね。
だからAPと重なるのは、AP’になって(教科書の用語では「対応する辺の長さは等しい」と言うよ)、AP=AP’ということがわかるね。
これで、「円外の1点から、その円に引いた2つの接線の長さは等しくなる」という性質が説明できたね。
円と円への接線の性質
円外の1点から、その円に引いた2つの接線の長さは等しくなる

AP=AP’になるということだね。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


