「平方根」と「根号」とは？ルートの意味をわかりやすく解説

中学校３年生の数学で学習する「平方根」について、「根号」とは何か？ルートの記号の書き方や注意点、ルートでの平方根の表し方などをわかりやすく解説するよ。

平方根とルートの違いなどもくわしく説明するよ。

「平方根」と「根号」とは？ ルートの意味をわかりやすく解説のPDF（8枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 平方根とは
• 根号とは
• 近似値とは

平方根とは

「平方根へいほうこん」とは何かを考えるために、「平方」と「根」にわけて考えてみよう。

だから「平方根」とは、「２乗する前の、根っことなる数（もとになる数）」のことだよ。
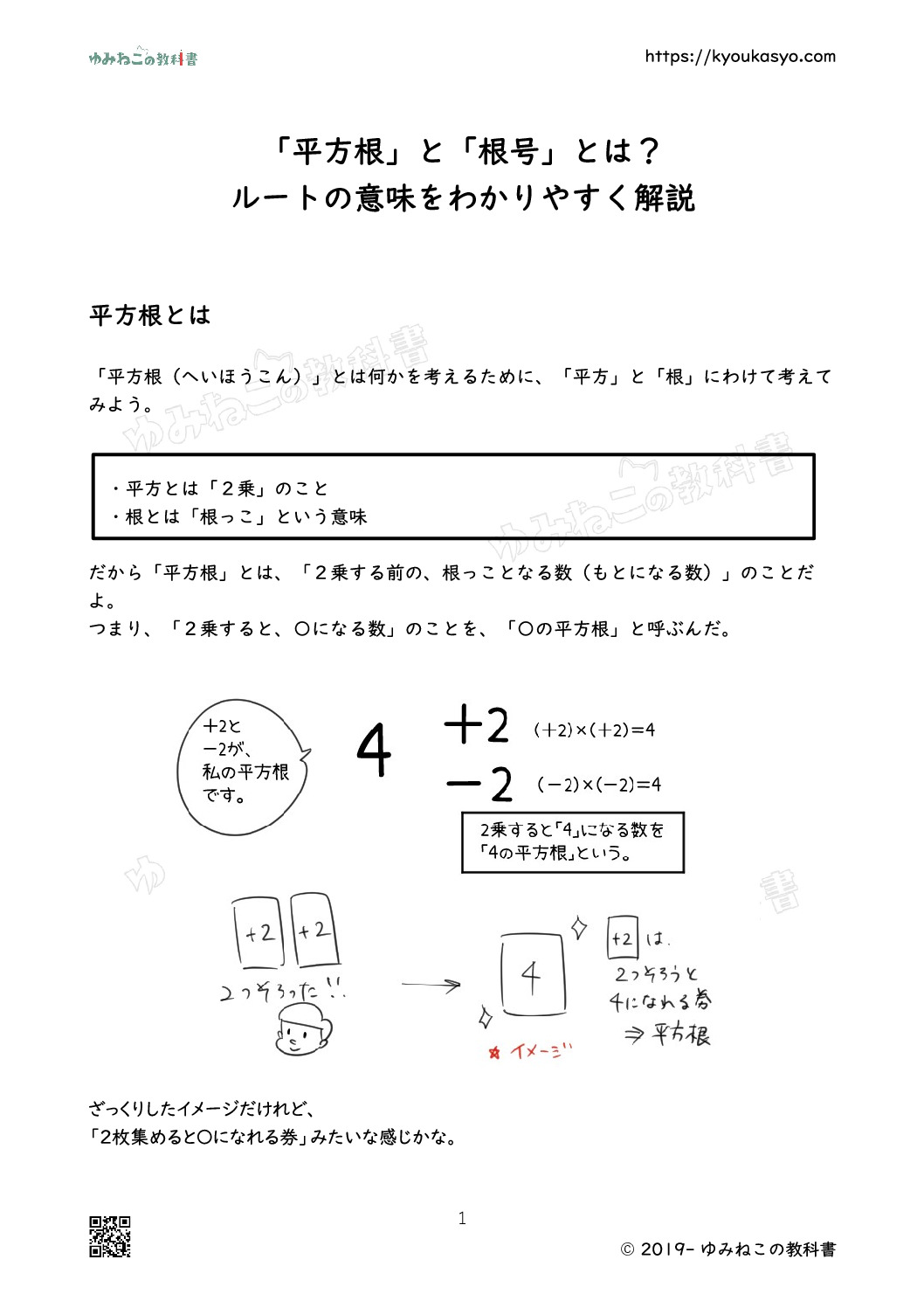
つまり、「２乗すると、〇になる数」のことを、「〇の平方根」と呼ぶんだ。

くまごろう

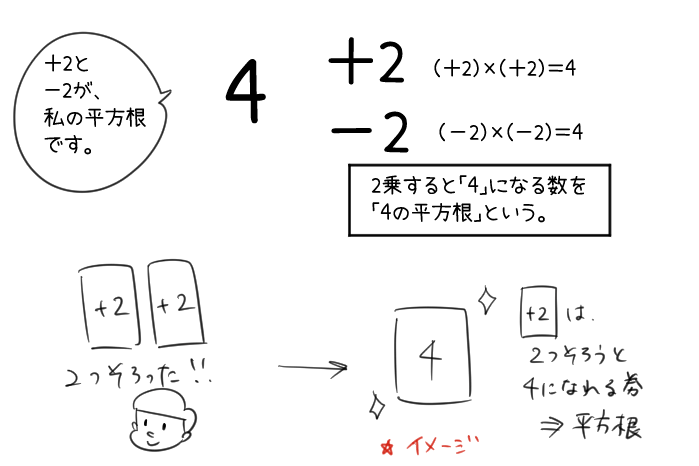
ざっくりしたイメージだけれど、
「２枚集めると〇になれる券」みたいな感じかな。

平方根を理解するために、簡単な例をあげてみるよ。

平方根の例

（問１）４の平方根は？

２乗して（２回かけて）４になる数だから、４の平方根は「－２」と「＋２」だよ。

「２乗したら４になる数」と聞かれると、「＋２」はすぐに思いつくかもしれないね。ただ、「－２」も２乗したら４になるよね。

平方根は、「－（マイナス）」と「＋（プラス）」の２つあるということをまずは覚えよう！

（問２）９の平方根は？

２乗して（２回かけて）９になる数だから、９の平方根は「－３」と「＋３」だよ。

（問３）１６の平方根は？

２乗して（２回かけて）１６になる数だから、１６の平方根は「－４」と「＋４」だよ。

くまごろう

ちなみに、「－２」と「＋２」とか、それぞれ書くのではなくて、マイナスとプラスをまとめて「±２」というふうに書いたりもするよ。

（問４）\(\frac{２５}{３６}\)の平方根は？

２乗して（２回かけて）\(\frac{２５}{３６}\)になる数だから、\(\frac{２５}{３６}\)の平方根は－\(\frac{５}{６}\)と＋\(\frac{５}{６}\)（±\(\frac{５}{６}\)）だよ。

平方根は「－（マイナス）」と「＋（プラス）」の２つあることがわかったね。

ただ、「０の平方根」は「０」１つだけだよ。そもそも、+０とか、－０とかないからね。

そして、負の数には、平方根が存在しないよ。
たとえば、２乗すると－９になる数、なんて存在しないよね。

根号（ルート）とは

平方根で登場する大事な用語の１つに「根号こんごう」というのがあるよ。
根号とは「平方根を表す記号」のことで、「\(\sqrt{}\)（ルート）」という記号を使うんだ。

「ルート」という言葉は、英語の「root」からきているよ。
「平方」の「根っこ」だから、「root（根っこ）」だね。

ルートの記号\(\sqrt{}\)も、「root」の「r」が形のもとになっているんだ。

ルートの書き方

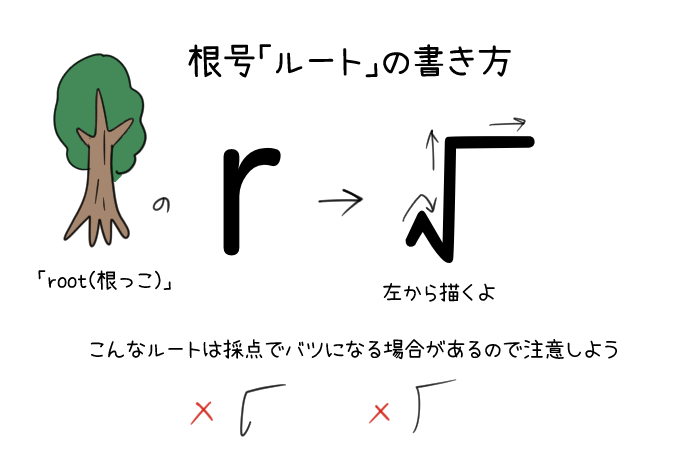
「ｒ」の形がもとになっているので、ルートの記号の書き方は、左はしから書いていくよ。

左のクネクネ曲がっている部分をきちんと書かないと、割り算のひっ算をするときの記号と見分けが付かなくなってしまったりするね。

書き方によっては、テストでバツになってしまったりもするので、注意してね。

根号（ルート）はどんなときに使うの？

さっき、「４の平方根」について考えたよね。

２乗して（２回かけて）４になる数は、－２と+２だったよね。

じゃあ、「３の平方根」はどうなるだろう？

くまごろう

２乗して（２回かけて）３になる数と言われても、見つからないよね。

「３の平方根」は、ちゃんと存在はしてはいるんだけれど、「整数」や「わかりやすい小数」なんかでは表すことができないんだ。

実際に３の平方根を計算して求めてみると、「２乗すると３になる数」は「1.73205080757…」というように、小数点以下の数字がずーっと続いてしまって、割り切ることができないんだよ。

そうすると、「３の平方根」を表すのに困ってしまうよね。

そんなときに登場するのが根号の「\(\sqrt{}\)（ルート）」だよ。

\(\sqrt{}\)ルートを使えば、「３の平方根（２乗して３になる数）」は「±\(\sqrt{３}\)（ルート３）」と表すことができるんだ。

根号（ルート）を使って平方根を表してみよう

（問１）６の平方根は？

２乗して（２回かけて）６になる数は、－\(\sqrt{６}\)と＋\(\sqrt{６}\)だよ。

（問２）７の平方根は？

２乗して（２回かけて）７になる数は、－\(\sqrt{７}\)と＋\(\sqrt{７}\)だよ。

（問３）９の平方根は？

２乗して（２回かけて）９になる数は、－\(\sqrt{９}\)と＋\(\sqrt{９}\)だよ。

ただ、このあとくわしく説明するけれど、「２乗して９になる数は、整数で表す」こともできて、－３と+３になるよね。

根号を使わずに表す

さっき、かんたんに説明したとおり、９の平方根について考えてみよう。

９の平方根は根号を使うと「－\(\sqrt{９}\)」と「＋\(\sqrt{９}\)」になるんだけれど、「２乗すると９になる数」は、整数の「－３」と「+３」で表すこともできるよね。

このことから次のことがわかるよ。

１６の平方根のばあいはどうだろう？

１６の平方根は根号を使うと「－\(\sqrt{１６}\)」と「＋\(\sqrt{１６}\)」になるんだけれど、「２乗すると１６になる数」だから、整数の「－４」と「+４」で表すこともできるね。

このことから次のことがわかるよ。

９の平方根と１６の平方根について考えてみてわかることは、

「\(\sqrt{}\)」の中の数字が、「ある数を２つかけ合せたもの」というふうに表すことができるのであれば、「\(\sqrt{}\)」を外すことができるんだよ。

\(\sqrt{９}\)だったら、\(\sqrt{３×３}\)と表せるよね。

「\(\sqrt{}\)」の中に「３」が２つかけあわされているから、「\(\sqrt{}\)」が外れて「３」になるんだ。

そもそも、根号（ルート）は、平方根を整数で表すことができないときに使うための記号だよね。

だから、平方根が整数になるのであれば、根号（ルート）を使う必要がないということだね。

同じように根号を使わずに表すことができる数の一部を紹介するね。
（つまりは、平方根が整数の数ということだよ）

「\(\sqrt{}\)」の中が何かの２乗になっているときは、根号を使わずに表すことができる可能性が高いことを覚えておこう。

「\(\sqrt{}\)」と「－\(\sqrt{}\)」の違い

根号（ルート）には、プラスとマイナスがあるよ。

ここで注意してほしいのは、たとえば、「４の平方根」というと、「±２」だったよね。＋２も、－２もどちらも４の平方根だよね。

では、「\(\sqrt{4}\)」はというと、これは「＋２」しかあてはまらないんだ。
おなじく「－\(\sqrt{4}\)」はというと、これは「－２」しかあてはまらないよ。

これは、「平方根」という言葉と「ルート」という言葉は、細かい意味が違うからなんだ。

「平方根」と「ルート」の違い

「平方根」は、「２乗すると、〇になる数」だから、プラスとマイナス両方あてはまるんだ。

それに対して、「ルート」は、「２乗すると、〇になる正の数」という意味なんだ。「正の数」という情報が加わっているんだよ。

だから、「ルート４（\(\sqrt{4}\)）」とは、「２乗すると４になる正の数」なので、「＋２」しか当てはまらないんだよ。

根号（ルート）の前に－（マイナス記号）をつけてあげることで、「２乗すると４になる負の数」という意味にすることができるんだ。

だから、「－ルート４（－\(\sqrt{4}\)）」は、「２乗すると４になる負の数」なので、「－２」しか当てはまらないというわけだね。

近似値とは

近似値とは、 本当の値ではないけれど、「それに近い値」のことだよ。

平方根は、きれいに整数で表すことができる場合もあれば、そうでない場合もあったよね。

たとえば、２乗して２になる数は「1.41421356237…」となってしまって永遠に終わらない小数なんだ。
だから、根号を使って「\(\sqrt{２}\)」と表すんだったよね。

根号を使って表してもいいけれど、ずっと続いてしまう小数のある程度のところまでで切って表す方法もあるんだ。
それが、「近似値」だよ。

中学数学では、ずっと少数が続いてしまうような平方根を、とりあえずだいたいの値である近似値で計算する問題が出たりするんだ。

問題文で「〇〇の平方根の近似値は△△とする」と指示してくれることもあるけれど、これから紹介する平方根の近似値は「覚えいる」ことを前提として問題にだされることもあるので、暗記しておくと安心だよ。

代表的な平方根の近似値の覚え方

中学校では最低限、次の近似値は覚えておくといいよ。

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。