「因数分解を使った二次方程式の解き方」を例題を使って徹底解説
中学3年生の数学で学習する二次方程式について、因数分解の考え方を使って二次方程式を解く方法をわかりやすく解説しているよ。
(x-a)(x+b)=0のニ次方程式の解き方
今までにニ次方程式を解く方法を2つ勉強してきたよね。
- 1つ目が平方根の考えを使った方法
- 2つ目が解の公式を使った方法
解の公式はどんなニ次方程式であったも「これさえ知っていればなんとかなる」という便利アイテムだったよね。
解の公式の復習をしてみよう。
x2+5x+4=0を解の公式を使って解いてみよう
ax²+bx+c=0と比べると
a=1、b=5、c=4であることがわかるね。
この3つの値を解の公式に代入しよう。
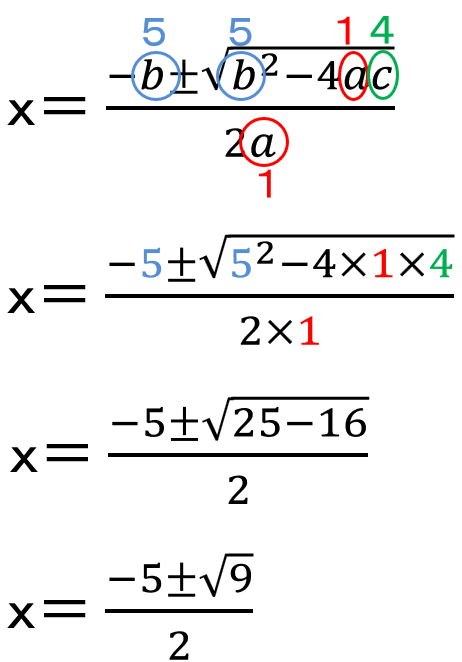
\(\sqrt{9}\)=3になるから、もう少し計算することができるね。
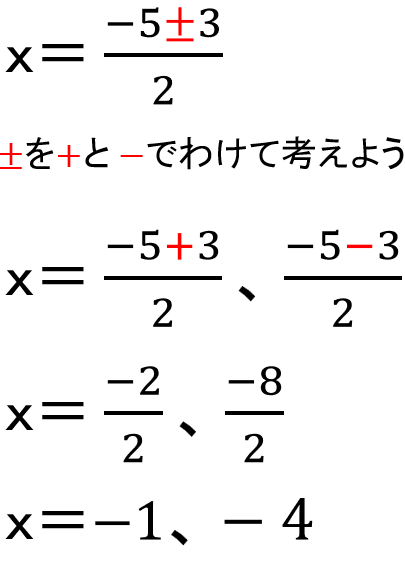
x2+5x+4=0がx=-1とx=-4であることがわかったね。
ただ、解の公式ってすごく計算がめんどくさいよね。
実はx2+5x+4=0のようなニ次方程式だったら解の公式を使わずに簡単に解を求めることができるんだよ。
x2+5x+4=0を因数分解を使って解いてみよう
x2+5x+4=0の左辺に注目しよう。
x2+5x+4って因数分解できるよね。
x2+5x+4=(x-1)(x-4)
だからニ次方程式は次のように変形できるよ。
x2+5x+4=0
(x-1)(x-4)=0
この式って
(x-1)×(x-4)=0のことだよね。
この式をわかりやすく文章にすると
「(x-1)と(x-4)をかけたら0になるよ。そのときxの値っていくつになるかな」
ということだよね。
(x-1)と(x-4)をかけたら0になるってことは、どちらかが0になったらいいよね。
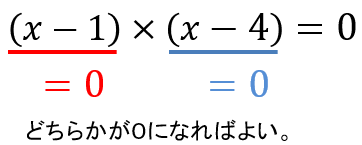
だから
①(x-1)=0になるか
②(x-4)=0になるか
そうすると2次方程式の解は
①(x-1)=0 → x=1
②(x-4)=0 → x=4
と求められるよ。
解の公式を使って解くよりも簡単に解けたんじゃないかな?
解の公式を使う前に、因数分解ができないかを考えよう。
ポイント
(x-a)(x+b)=0のように因数分解できるとき
解はx=a、x=-bになる。
(x-a)(x+b)=0の練習問題
(1)(x-3)(x-2)=0を解きなさい。
(x-3)×(x-2)=0のことだから、
x-3=0になるか、x-2=0になればいいよね。
だから2次方程式の解は
x-3=0 → x=3
x-2=0 → x=2
になるよ。
(2)(x+3)(x-2)=0を解きなさい。
(x+3)×(x-2)=0のことだから、
x+3=0になるか、x-2=0になればいいよね。
だから2次方程式の解は
x+3=0 → x=-3
x-2=0 → x=2
になるよ。
(3)(x-2)2=0を解きなさい。
(x-2)×(x-2)=0のことだから、
x-2=0になればいいよね。
だから二次方程式の解は
x-2=0 → x=2
二次方程式ってだいたいの問題で解が2つになるんだけど、(x-2)2=0みたいな(x-a)2=0の形に因数分解できるときは解が1つになるんだ。
解が1つになることを「重解」っていうんだよ。
漢字を見てもらったらわかると思うけど「解が重なっている」っていう意味だね。
(x-2)2=(x-2)(x-2)ということだから、x=2が重なっていると考えればいいね。
(4)x2+3x+2=0を解きなさい。
左辺を見たら因数分解できることがわかるね。
x2+3x+2=(x-1)(x-2)
2次方程式は
x2+3x+2=0
(x-1)(x-2)=0
になるよ。
(x-1)×(x-2)=0のことだから、
x-1=0になるか、x-2=0になればいいよね。
だから二次方程式の解は
x-1=0 → x=1
x-2=0 → x=2
になるよ。
(5)x2-25=0を解きなさい。
左辺を見たら因数分解できることがわかるね。
x2-25=(x+5)(x-5)
2次方程式は
x2-25=0
(x+5)(x-5)=0
になるよ。
(x+5)×(x-5)=0のことだから、
x+5=0になるか、x-5=0になればいいよね。
だからニ次方程式の解は
x+5=0 → x=-5
x-5=0 → x=5
になるよ。
x2=axのニ次方程式の解き方
x2=3xみたいな形のニ次方程式ってすごく間違えやすいんだ。間違えの例を紹介するね。
x2=3xの間違いの例
両辺をxで割って
x2÷x=3x÷x
x=3
間違ってることが分かりづらいかもしれないけれど、この解き方はダメなんだ。
どこが違うのかというと
「両辺をxで割る」
方程式の問題で「両辺を文字で割る」っていうのはかなり危険な行為だと覚えておこう。
その理由は文字が0になるかもしれないから
算数や数学の世界では「0で割ってはいけない」という決まりがあるんだよ。
もし、xが0だった場合、その決まりを破ることになるから、「両辺をxで割る」というところが間違っているんだよ。
0で割ってはいけない理由
小学生でもわかるように0で割ってはいけない理由を考えてみよう。
あたりまえだけど
6÷3=2だよね。
この式って
3×2をしたら元の6に戻るよね。
同じように
12÷6=2だよね。
この式って
6×2をしたら元の12に戻るよね。
じゃあ
6÷0を考えよう。
もし6÷0=◇になったとしたら
0×◇をしたら6になるってことだよね。
ただ、0にどんな数をかけても6にはならないよね。だから、6÷0はできないということになるんだよ。
0で割ってはいけないということは覚えておこう。
x2=axの二次方程式の解き方
x2=3xを解くには、まず(右辺)の3xを移項しよう。
x2=3x
x2-3x=0
次に共通因数xでくくろう。
x2-3x=0
x(x-3)=0 ←展開したら上の式に戻ることは確認しておこう。
この式って
x×(x-3)=0のことだから、
x=0になるか、x-3=0になればいいよね。
だから2次方程式の解は
x=0
x-3=0 → x=3
になるよ。
x2=axの練習問題
x2=-5xを解きなさい。
まず(右辺)の-5xを移項しよう。
x2=-5x
x2+5x=0
次に共通因数xでくくろう。
x2+5x=0
x(x+5)=0 ←展開したら上の式に戻ることは確認しておこう。
この式って
x×(x+5)=0のことだから、
x=0になるか、x+5=0になればいいよね。
だから2次方程式の解は
x=0
x+5=0 → x=-5
になるよ。
「因数分解を使った二次方程式の解き方」まとめ
(x-a)(x+b)=0のように因数分解できるとき
解はx=a、x=-bになる。
方程式の問題で「両辺を文字で割る」ことは文字が0になるかもしれないため、してはいけないことに注意しよう。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


