相似の利用「木の高さを求める」「縮図」の問題の解き方を徹底解説
中学３年生の数学で学習する「相似の利用」について、相似な図形の特徴や性質を使って、「木の高さを求める」問題、「建物の高さを求める」問題、「見上げる」問題、そして「縮図を描く」問題の解き方やポイントをわかりやすく解説するよ。
目次
相似の利用「木の高さを求める」問題
「相似の利用」の単元では、このように「木の高さを求める」問題がよく出題されるよ。
相似な図形の性質を使って、木の高さを求める方法を説明するね。
公園にいる身長1.7mの人のかげの長さが1mのとき、同じ公園にある木のかげの長さが5ｍだった。この木の高さを求めよ。
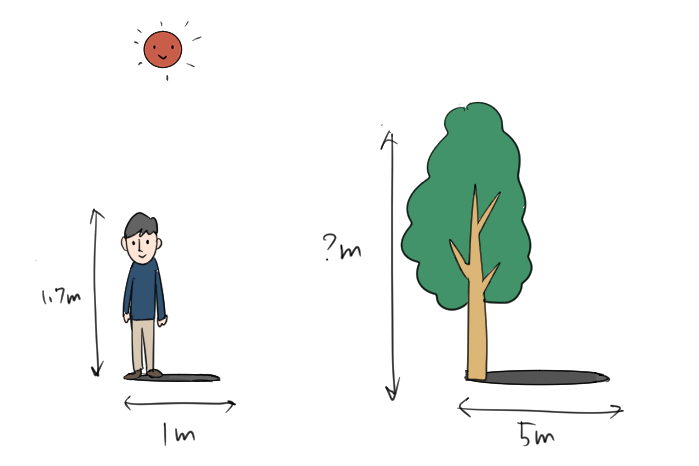
木の高さを知りたいんだけれど、直接測ることができないとき、「かげ」を利用して、木の高さを求められないかな？というわけだね。
木の高さを求める問題のポイントは
「高さ」と「かげ」を含む三角形はそれぞれみんな「相似になる」ということ。
実は「人の高さ」と「人のかげ」の先端を結んだ三角形と、「木の高さ」と「木のかげ」の先端を結んだ三角形は相似になるんだ。
なぜかというと、木と人が同じ場所にいる場合、太陽の光の当たり方は同じになるからだよ。
相似になる理由
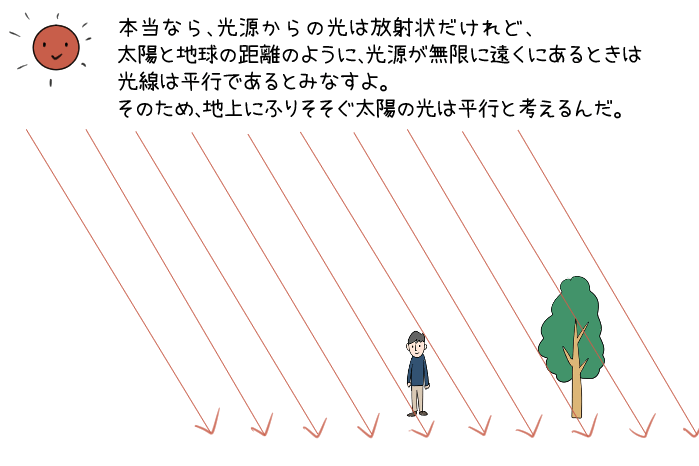
太陽の光は、平行に進むんだ。
そして太陽は、「人と木の距離」とは比べ物にならないくらい遠くにあるよね。ということは、人にも木にも同じように光が当たっていると考えていいんだよ。
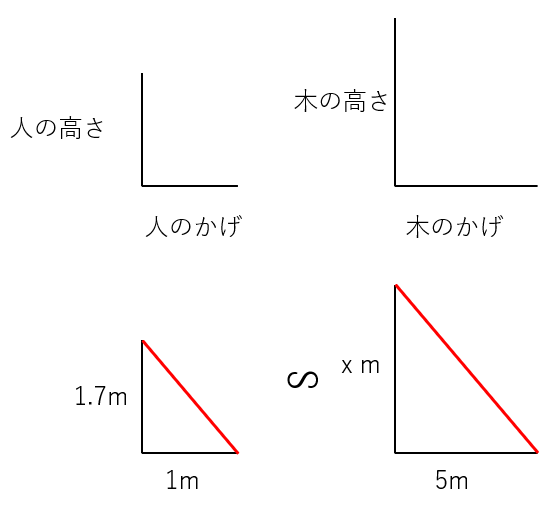
今回求めたいのは「木の高さ」だから、木の高さをxmと置いたよ。
ちなみに相似条件は「２組の角がそれぞれ等しい」
①人も木も地面に垂直に立っていると考える「∠A＝∠E＝90°」
②太陽の光線（赤線）は平行に当たっているので、「∠C＝∠F」
①②から２組の角がそれぞれ等しいから、△ABC∽△DEF
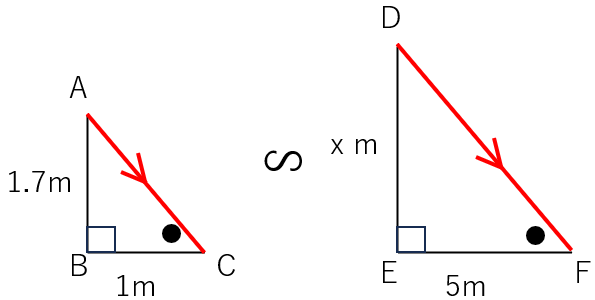
あとは相似の性質を使ってxを求めたらＯＫだね。
ｘは長さの部分だから、相似の性質「相似な図形の対応する辺の長さの比はすべて等しい」が使えそうだね。
相似な図形の性質
相似な図形の対応する辺の長さの比はすべて等しい。
相似な図形の対応する角の大きさはそれぞれ等しい。
対応する辺の比は等しいから、
1.7:x=1:5という比例式を立てることができるよね。
1.7:x=1:5 ←比例式の性質「a:b=c:d →ad=bc」を使うよ。
x×1=1.7×5
x=8.5
木の高さは8.5mと求めることができたね。
相似の利用「建物の高さを求める」問題
相似の利用の単元では、木の高さを求める問題もよく出題されるけど、このように「建物の高さ」を求める問題もあるんだ。
ただ、解き方は同じになるよ。
高さ2mの鉄棒のかげが1.5mのとき、建物のかげが30ｍだった。この建物の高さを求めよ。
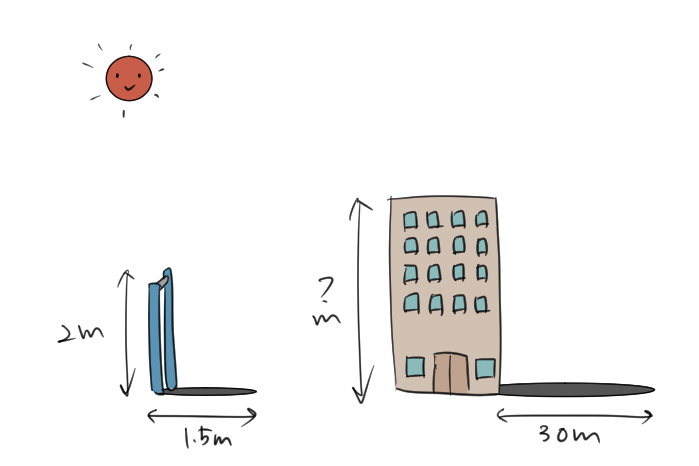
建物の高さを知りたいんだけれど、直接測ることは難しいよね。「かげ」を利用して、建物の高さを求められないかな？というわけだよ。
今回の問題のポイントも、木のかげの問題と同じで
かげは相似になるということ。
「鉄棒の高さ」と「鉄棒のかげ」の先端を結んだ三角形と、「建物の高さ」と「建物のかげ」の先端を結んだ三角形は相似になるんだ。
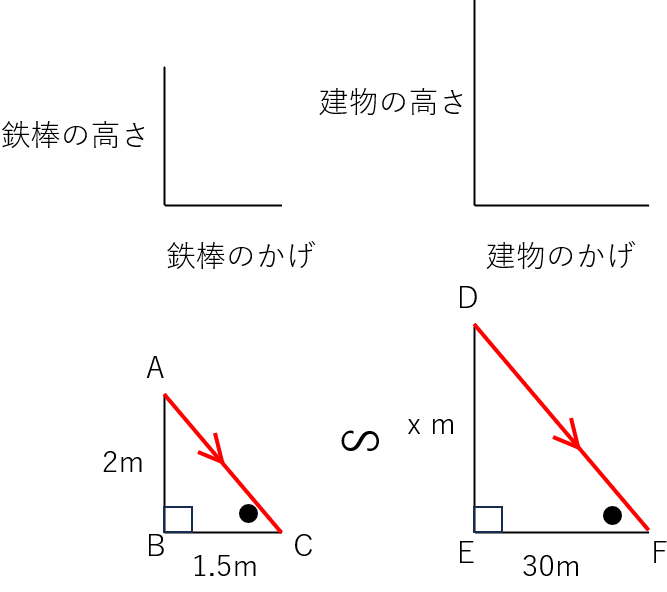
今回求めたいのは「建物の高さ」だから、建物の高さをxmと置いたよ。
あとは相似の性質を使ってxを求めればＯＫだね。
対応する辺の比は等しいから、
2:x=1.5:30という比例式を立てることができるよね。
2:x=1.5:30
x×1.5=2×30
1.5x=60 ←両辺を1.5で割ろう
x=40
建物の高さは40mと求めることができたね。
相似の利用「見上げる」問題
木の高さを求める問題で少しレベルアップしたのが、「見上げる問題」だよ。
ある建物の高さを測るために、建物と20mはなれた地点から建物の頂上を見上げたら、その角度は40°だった。
縮図を書いて、この建物の高さを求めなさい。ただし、目の高さを1.5mとする。
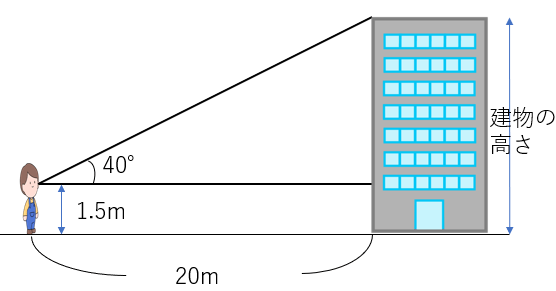
上の図をもっと簡潔に書いてみると次のようになるよね。今回の計算で大事なところは目線より上のところだから、下の部分と建物は省略したよ。
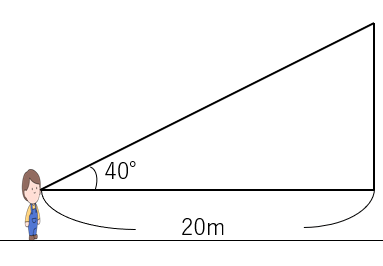
では実際に建物の高さを求めよう。
縮図っていうのは、実物よりも大きさを小さくした図のことだよ。
どのくらい小さく書くかはノートの大きさ次第って感じかな。
例えば、1/10の縮図を書くとすると、人と建物の距離は20m×1/10=2mになるね。
２ｍともなると、ノートに書くことができないから、もっと縮小する必要があるよね。
だから今回は1/100の縮図を書くことにしよう。
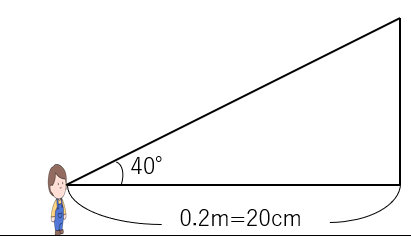
20mを1/100にすると、20m×1/100=0.2m。
0.2mとは20cmのことだから、上の三角形の底辺は20cmになるよ。
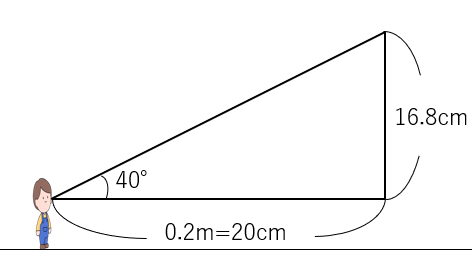
この三角形の高さを測ってみよう。
正確に三角形をかけていたら、16.8cmになると思うよ。
縮小する前の三角形（縮図）と縮小した三角形を比較してみよう。
縮図 実際の長さ
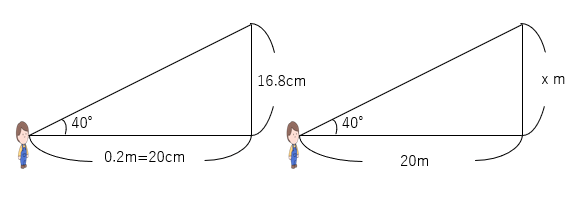
縮小しただけだから2つの三角形は相似になるよね。
求めたい三角形の高さをxmとおいて、相似な図形の性質を使って、xを求めよう。
相似な図形の性質
相似な図形の対応する辺の長さの比はすべて等しい。
相似な図形の対応する角の大きさはそれぞれ等しい。
ただ、単位が違うから「m」にそろえたよ。
縮図 実際の長さ
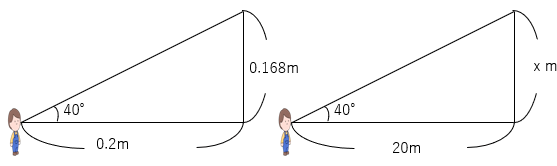
対応する辺の比は等しいから、
0.2:20=0.168:xという比例式を立てることができるよね。
0.2:20=0.168:x
0.2×x=20×0.168
0.2x=3.36
2x=33.16
x=16.8
実際の長さのxが16.8mって求まったね。
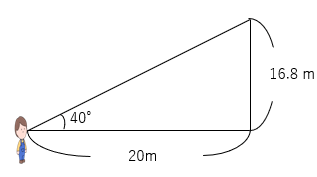
最初の図で今回わかった16.8mを書き入れてみよう。
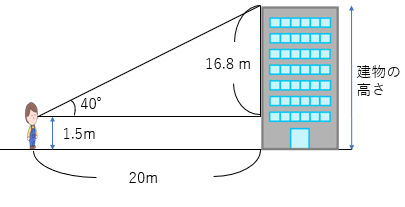
答えを「建物の高さ16.8m」としてしまったら間違いだよ。上の図をみてわかると思うけど、人の目線の高さを足さないといけないよね。
だから16.8に1.5を足すよ。
16.8+1.5=18.3
建物の高さは18.3mと求めることができるね。
相似の利用「縮図を描く」問題
もう一問、縮図を描いて長さを求める問題に挑戦してみよう。
ある池のＡ地点とB地点の距離を測りたい。
A地点から30m、B地点から50mのところにＰ地点をとり、∠APBの大きさを測ったら85°だった。このとき、A、B間の距離を求めなさい。
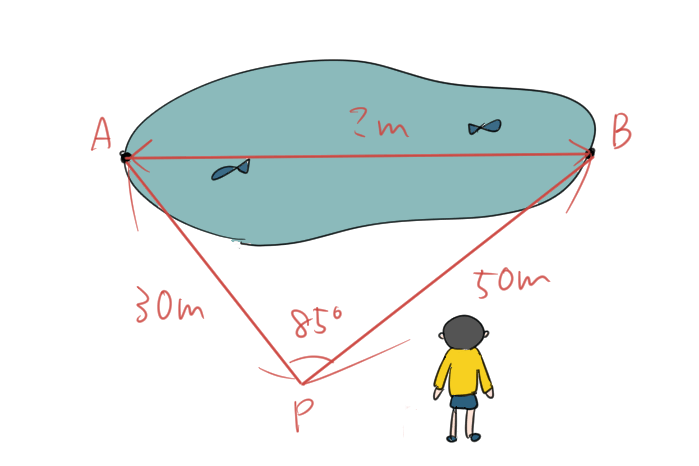
上の図をもっと簡潔に書いてみると次のようになるよね。
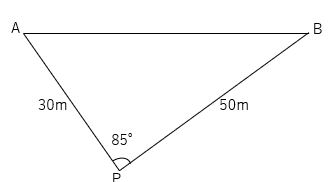
じゃあ実際にABの距離を求めよう。
1/10の縮図を書くとすると、BPの距離は50m×1/10=5mになるよ。
5mではノートに書くことができないから、今回ももっと縮小する必要があるよね。
今回は1/1000の縮図で書くことにしよう。
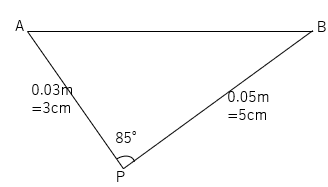
30mを1/1000にすると、30m×1/1000=0.03m。0.03mは3cmのことだね
50mを1/1000にすると、50m×1/1000=0.05m。0.05mはcmのことだよね。
この三角形のABの長さを定規で測ってみよう。
正確に三角形をかけていたら、5.6cmになると思うよ。
ここから、相似の性質を使って、実際のABの距離を求めてもいいけど、今回は違う方法で解いてみよう。
1/1000の縮図を描いたのだから、もとの実際の距離を求めるには、1000倍してあげればいいよね。
縮図の5.6cm
↓ ×1000
実際の5.6×1000=5600cm=56m
と求めることができるよ。
池のAB間の距離は56mだね。
「相似の利用の問題の解き方」まとめ
- 高さと影をもとに考える問題のポイント
→「高さ」と「かげ」を含む三角形はそれぞれみんな「相似になる」
→相似な図形の性質「相似な図形の対応する辺の長さの比はすべて等しい」を使ってわかっていな部分の長さを求めることができる。 - 「見上げる問題」では、高さを求めるのに「人の目線の高さ」を足さないといけないことに注意しよう
- 「縮図を書く問題」では、もとの大きさをどのくらい縮小すればいいかを考えよう。
運営者情報
ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。
