相似な図形とは?相似の記号・相似な図形の性質をわかりやすく解説
中学校3年生の数学で学習する「相似な図形」について、相似な図形の性質や、相似な図形であることを示す記号の書き方や使い方をわかりやすく解説するよ。
中学2年生で学習した「合同」との違い、相似比の求め方などくわしく紹介しているよ。
相似とは
「そうじ」って聞くと、部屋をきれいにする「掃除」を想像する人もいるかもしれないけれど、数学の「そうじ」は、図形の「相似」のことだよ。
「相似」とは何かを漢字から考えてみよう。
「相」・・・相手
「似」・・・似ている
だから相似とは「相手と似ていること」。
つまり、「そっくりさん」のイメージだね。
もう少し丁寧に説明すると、数学で学習する相似とは、「同じ形のまま拡大・縮小したりしている」ことで、同じ形のまま拡大や縮小した図形のことを「相似な図形」と呼ぶよ。
ポイントは「同じ形のまま」ということ。
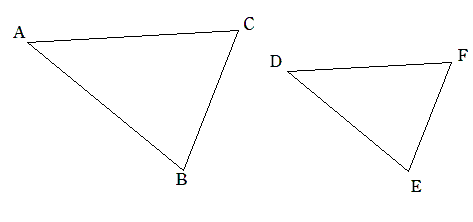
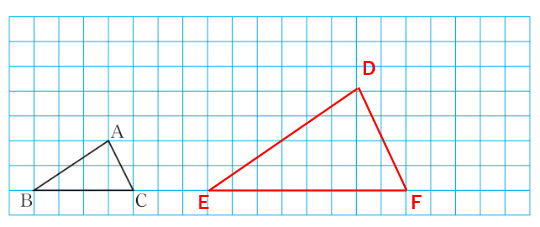
下の2つの三角形を見てみよう。
△ABCを縮小した図形が△DEFだよ。この2つの三角形は同じ形だから、「相似な図形」だと言えるよ。
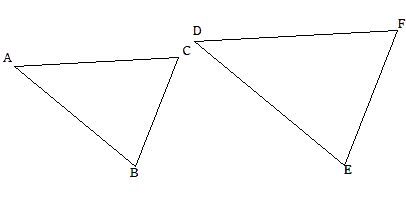
次に△ABCを拡大した図形が△DEFになっている場合。
この2つの三角形も、同じ形だから「相似な図形」だよ。
なんとなく「相似」とは何かがわかってきたかな?
「相似な図形」とは?
- 相似とは、同じ形のまま拡大・縮小したりすること
- 同じ形のまま拡大や縮小した図形のことを「相似な図形」と呼ぶ
合同な図形も相似
「相似」は、2年生で学習した「合同」と少し似ているところがあるから、合同についても復習しよう。
合同というのは「2つの図形がぴったり重なること」だったよね。
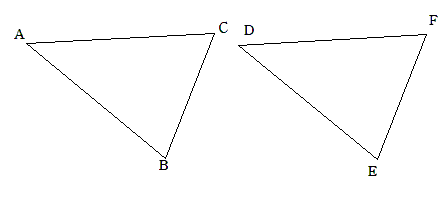
実は、合同な図形も相似な図形といえるんだ。
だって△ABCを同じ形のまま1倍に拡大した図形が△DEFだから、2つの図形は相似とも言えるよね。
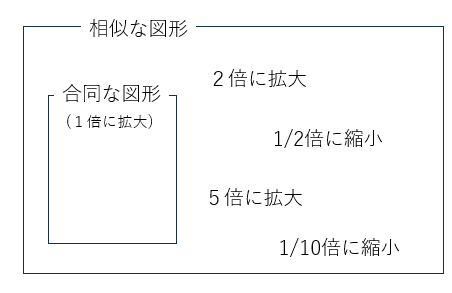
相似と合同のイメージは下のような感じで、相似な図形の中に合同な図形があるんだよ。
相似であることを表す記号と使い方

△ABCと△DEFは相似だったよね。
この2つの三角形が、相似な図形であることを、記号で表すことができたら便利だよね。
2年生で学習した「合同」では、合同の記号「≡(ごうどう)」があったよね。
同じように「相似」にも、相似を表す記号「∽(そうじ)」があるんだ
相似であることを表す記号「∽」
- 「相似」や「類似している」ことを意味する英語の「similar」の頭文字「S」を横にしたといわれているよ
相似の記号「∽」の使い方
相似の記号をどのように使うかを紹介するね。

△ABCと△DEFが相似だったとしたら次のように表すよ。
△ABC∽△DEF (読み方 三角形ABC 相似 三角形DEF)
相似の記号と合同の記号の関係
実は、相似の記号「∽」と合同の記号「≡」には関係があるんだよ。
実は合同の記号「≡」は、昔は次のように表していたんだよ。
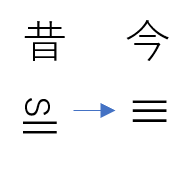
合同の記号の由来
- 合同な図形は相似でもあるため「∽」がついている
- 合同な図形は、面積が等しくなるから「=」がついている
同じ形(相似)で面積が等しいから、「∽」に「=」がついた記号だったんだね。
それが、現在はすべてが線になって、「≡」という記号になったよ。
相似な図形の性質
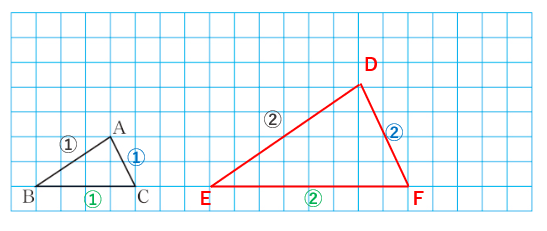
下の△ABCを同じ形のまま2倍に拡大した△DEFを書きなさい。

すべての辺の長さを2倍して書けばいいから次のようになるよ。
2つの三角形を見ると、次のことがわかるよね。
相似な図形の性質
辺の長さ
AB:DE=1:2
BC:EF=1:2
CA:FD=1:2
→すべて1:2になっているように、相似な図形の「対応する辺の長さの比はすべて等しい」。
角の大きさ
∠A=∠D
∠B=∠E
∠C=∠F
→相似な図形の対応する角の大きさはそれぞれ等しい。
相似比とは
相似な図形の対応する辺の長さの比のことを「相似比」と呼ぶよ。
今回の問題だったら、相似比は1:2になるよ。
相似比の練習問題
テストでは、相似な図形の相似比がいくつであるかを求める問題が出るよ。
試しにチャレンジしてみよう。
問 △ABCと△DEFは相似であるとき、相似比を求めなさい。
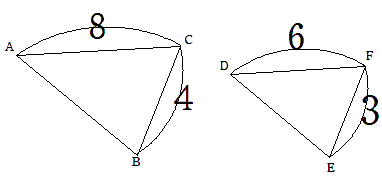
辺ACと対応する辺は辺DFなので、相似比は8:6になるね。
8:6=4:3だから
答えは4:3だよ。
辺BCと辺EFの長さの比からも相似比は求められるよ。
「相似な図形」まとめ
相似とは、同じ形のまま拡大・縮小したりすること
同じ形のまま拡大や縮小した図形のことを「相似な図形」と呼ぶ
相似な図形であることを表すには、「∽」の記号を使う
例:△ABCと△DEFが相似な図形の場合、△ABC∽△DEFと表す
相似な図形の「対応する辺の長さの比はすべて等しい」
相似な図形の対応する角の大きさはそれぞれ等しい
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


