測定値の表し方を解説「真の値の範囲」「誤差」「有効数字」とは?
中学3年生の数学で学習する「測定値の表し方」について、「真の値の範囲」「誤差」とはなにか、「有効数字」の考え方や表し方、有効数字の問題の解き方をわかりやすく解説するよ。
真の値の範囲とは
真の値とは
真の値っていうのは、「真実」の「真」という漢字からもわかるように「真実の値」だよ。
もう少しわかりやすく言うと、「本当の長さ」「本当の重さ」のこと。
「えっどういうこと」って思う人もいると思うから例を出して考えてみよう。
例えば、ある長さを1mm単位の定規で測って「2.8mm」だったとしよう。
小学校までは「2.8mmなんだね」で終わっていたけど、中学校のこの単元ではさらに突っ込んで考えるよ。(他の単元だったら、2.8mmとして考えるんだけどね)
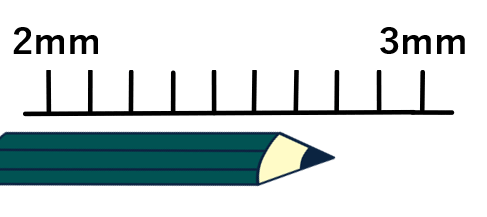
実は
定規で読み取った値は不確かな数になるよ。
だって、よーく拡大して目盛りを見たら、「2.78mm」かもしれないし、「2.83mm」かもしれない。
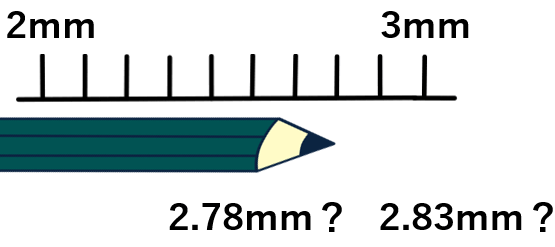
極端なことを言ったら、「2.800001mm」かもしれないよね。
もはや人の目だったり定規の限界だね。
こんな感じで何かの長さや重さを測るときは「真の値」を求めることは難しいんだよ。
近似値とは
そこで登場するのが「近似値」。
近似値っていうのは、真の値に限りなく近い値のことだよ。
よーく拡大してみたら2.78mmや2.83mmや2.800001mmに見えてきてしまい、キリがないよね。
だから近似値は2.8mmとして長さを測ったことにしていたんだよ。(この単元以外では、これでおしまいだったよね。)
真の値の範囲とは
真の値を測って求めることは難しいから、真の値はだいたい〇~◇の範囲の中にあるだろうと考えよう。
この範囲のことを「真の値の範囲」っていうよ。
もう少しわかりやすく言うと、
真の値の範囲っていうのは、どこからどこまでが四捨五入して近似値2.8mmとして考えていいか?ってことだよ。
例えば、次の問題を考えてみよう。
近似値2.8mmの真の値aの範囲を求めよ。
近似値が2.8mmと測って求めたんだけど、本当の値(真の値)を求めるのは難しいんだったよね。だから本当の値(真の値)はだいたい〇~◇の範囲にあると考えよう。
近似値が2.8mmということは小数第2位を四捨五入して2.8mmになっているから、2.71や2.86は範囲にないよ。
だって、2.71を四捨五入したら「2.7」になるし、
2.86を四捨五入したら「2.9」になるからね。
真の値の範囲の最も小さい数を見つける
小数第2位を四捨五入して2.8mmになる最も小さい数を考えよう。
2.74だと四捨五入すると2.7
2.75だと四捨五入すると2.8になるね。
だから真の値の範囲の最も小さい数は「2.75」になるよ。
だから真の値aの範囲は次のように表せるよ。
2.75≦a
aが2.75になっても四捨五入して2.8になるから、「=(イコール)」が「<」の下についているよ。
真の値の範囲の最も大きい数を見つける
小数第2位を四捨五入して2.8mmになる最も大きい数を考えよう。
2.84だと四捨五入すると2.8
2.85だと四捨五入すると2.9になるね。
だから真の値の範囲の最も大きい数は「2.84」といいたいところだけど、注意が必要!!
2.843でも小数第2位を四捨五入したら2.8になるし
2.849でも小数第2位を四捨五入したら2.8になるよね。
つまり、2.85未満であれば、四捨五入したら2.8になるってこと。
だから真の値aは次のように表せるよ。
a<2.85
さっきと違うのは「<」の下に「=(イコール)」がないこと。「=」がないってことはa=2.85は入らないよ。
真の値の範囲を求める
真の値の最も小さい値と大きい値が求まったから2つを合体させて次のようになるよ。
2.75≦a<2.85
不等号の下に「=(イコール)」があるものとないものがあることに気をつけようね。
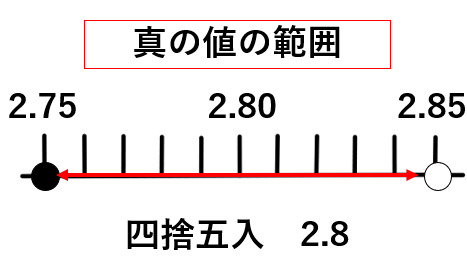
真の値の範囲とは
真の値を求めることは難しい。だから真の値はだいたいこのくらいだろうという「真の値の範囲」を求めたよ。
近似値2.8だったとすると、真の値の範囲は2.75≦a<2.85 になるよ。
2.75は四捨五入すると2.8になるけど、
2.85は四捨五入すると2.9になってしまうから、2.85の方には「<」を使って表すよ。
「誤差」とは
誤差っていうのは、本当の値(真の値)と近似値の差のこと。
だから次の式で求めることができるんだ。
(誤差)=(近似値)-(真の値)
さっきの問題だと、(近似値)は2.8mmで真の値の範囲は2.75≦a<2.85だったよね。
これを図に表すと次のようになるよ。
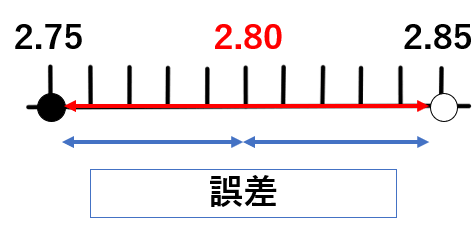
この問題での誤差はどんなに大きくても0.05mmになることがわかるね。
「有効数字」とは
「有効数字」というのは、「近似値を表す数字のうち、信頼できる数字」のこと。
「どこまでが信頼できる数字か」をはっきりさせるために、〇×10◇(1ケタの数字×10の累乗)という形で表すんだよ。
気をつけなくてはいけないのは、〇に入る数はもとの有効数字の一番上の1ケタまでの数なんだ。
※少数になるのはOK
どうして「〇×10◇」の形で表すのかとか、〇に入る数が一番上の1ケタだけなのかについては、説明するので安心してね。
有効数字で表す問題
「有効数字」の問題は、このようなパターンで出題されるよ。
ある重さの測定値52.1kgの有効数字が5、2のとき、〇×10◇という形で表しなさい。
あるものの重さを測ったら、「52.1kg」になったんだよね。
でも、この測定値のうち、確実と信頼できるのは「52.1」の「5」と「2」までなんだね。
「5」と「2」までは有効数字で信頼できるからいいけれど、「52.1」の「1」は有効数字ではないので、「0」にしてしまうよ。
「1」を「0」にすると「52.0」になるよね。
この「52.0」を「〇×10◇」という形で表すということだね。
〇は有効数字「52」の一番上の1ケタの数が入るから、この場合は「5」になるね。
「2」も有効数字だから、少数以下にちゃんと表すよ。
そうすると「5.2」になるね。
あとは、これに10の累乗をかけるから、
「5.2×10」となるね。
この「10の累乗」は、「5.2」がもとの値になるためには、10の何乗をかければいいのか、で考えるよ。
「5.2」を「52.0」にするには、10倍すればいいから、「5.2×10」で大丈夫だね。
では、次のような場合はどうだろう。
ある距離の測定値1843kmの有効数字が1、8、4のとき、〇×10◇という形で表しなさい。
ある距離の測定値「1843」のうち、「1」と「8」と「4」が有効数字で信頼できるから、残りの「3」を「0」にすると「1840」になるよね。
「1840」を「〇×10◇」という形で表すと次のようになるよ。
〇は有効数字「1840」の一番上の1ケタの数が入るから「1」が入るね。
残りの有効数字「8」「4」は少数点以下に表してあげると「1.84」になるね。
「1.84」がもとの「1840」になるには、1000倍すればいいね。
つまり、10の3乗をかければいいんだ。
なので、「1.84×103」と表せばOKだよ。
103=1000だから、1.84×103=1.84×1000=1840になっているよね。
ここで、どうして「〇×10◇」の形で表すのかとか、〇に入る数が一番上の1ケタだけなのかを改めて説明するよ。
どうして「〇×10◇」の形で表すのか
ひとつめの問題の答え「5.2×10」も、今の問題の答え「1.84×103」も、パッと見て「有効数字」がなにかわかるよね。
もしこれを普通に「52」と「1840」と表してしまうと、有効数字をのこした結果「52」なのか、それともただの2桁の数字「52」なのか、わからないよね。
「1840」なんて、本当は「1」「8」「4」までが有効数字なのに、見分けられないね。
でも、どちらも「〇×10◇」の形で表してあげることで、それぞれ「5」と「2」が有効数字、「1」「8」「4」が有効数字、と見分けることができるね。
「〇×10◇」の形は、有効数字がどこまでかをパッとわかるようにするために、そうやって表すようにしているんだね。
どうして一番上の1ケタだけなのか
「〇×10◇」の形で表す理由はわかったけれど、ではどうして〇に入るのは一番上の1ケタだけで、あとは小数点以下で表すのだろう。
これは、「表し方を揃えるため」が理由のひとつ。
「5.2×10」だったり、「18.4×102」だったり、〇の部分のケタ数がバラバラだと、混乱するよね。
パッ見て、「どちらの数が大きいか」もわかりづらいよね。
これが揃っていると、「5.2×10」と「1.84×103」で、10の3乗をかけている「1.84×103」のほうが大きい数だということがすぐに分かるね。
有効数字の問題には、こんな問題文のパターンもあるよ。
ある距離の測定値1843kmを有効数字2ケタで表せ。
今までと問題の聞き方が違うのは、「1」「8」が有効数字、というようにはっきり教えてくれなくて、「有効数字2ケタ」というところ。
でも、聞き方が違うだけで、つまり「上から2ケタ」という意味だよ。
だから「1843」の上から2ケタの「1」と「8」が有効数字で信頼できるってことになるよ。
残りの「4」と「3」を「0」にして表すと「1800」になるよね。
「1800」を〇×10◇という形で表すのに、一番上の1ケタの数「1」が入って、あとは小数点以下で表すので、「1.8」になるね。
「1.8」を本来の「1800」にするには、1000倍(103)すればいいから、「1.8×103」となるね。
有効数字は、「0」でも省略してはいけない
最後にこんなパターンはどうだろう。
同じ問題で、測定値が「1043km」だった場合をやってみよう。
ある距離の測定値1043kmを有効数字2ケタで表せ。
有効数字は上から2ケタまで、「1」と「0」だね。
残りを「0」で表すと、「1000」になるね。
「1000」を〇×10◇という形で表すのに、一番上の1ケタの数「1」が入って、あとは小数点以下で表すので、「1.0」になるね。
「1.0」を本来の「1000」にするには、1000倍(103)すればいいから、「1.0×103」となるね。
このパターンで気をつけなくてはいけないのは、「1.0」になったからといって、答えを「1×103」としてしまうミスだよ。
「1.0」だけれど、きちんと小数点以下の「0」まで表さなくてはいけないんだ。
どうしてかというと、「0」も有効数字だから。
「1.0」になったからといって、「1」にしてしまったら、有効数字が「1」だけということになってしまうよね。
つまり、もともとの有効数字がすべて表されるようにしなければいけないんだね。
「測定値の表し方」まとめ
- 「真の値」とは、「本当の長さ」や「本当の重さ」のこと。
- 「近似値」とは「真の値に限りなく近い値」のこと。
- 「真の値の範囲」とは「どこからどこまでが四捨五入して近似値として考えてよいかということで、真の値の最も小さい値と大きい値を求めて、次のように表す。
2.75≦a<2.85
不等号の下に「=(イコール)」があるものとないものがあることに気をつける。 - 「誤差」とは「本当の値(真の値)」と「近似値」の差のことで、次の式で求めることができる。
(誤差)=(近似値)-(真の値) - 「有効数字」とは「信頼できる数字」のことで、「〇×10◇」で表す。
〇には有効数字の一番上の1ケタの数が入り、残りは小数点以下で表す。
もとの数のケタ数にするために何十倍すればよいかを、10◇で表す。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


