「円周角と弧の定理」「直径と円周角の定理」をわかりやすく解説

中学３年生の数学で学習する、「円周角と弧の定理」「直径と円周角の定理」について、弧の長さが同じであれば円周角も等しくなる性質や、直径の円周角は９０°になる性質をわかりやすく解説するよ。それぞれの例題の解き方もくわしく紹介するよ。

「円周角と弧の定理」「直径と円周角の定理」を わかりやすく解説のPDF（12枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 円周角と弧の関係を調べてみよう
• 円周角と弧の定理
• 直径と円周角の定理
• まとめ

円周角と弧の関係を調べてみよう

前回「１つの弧に対する円周角の大きさは一定である」という円周角の定理を学習したね。

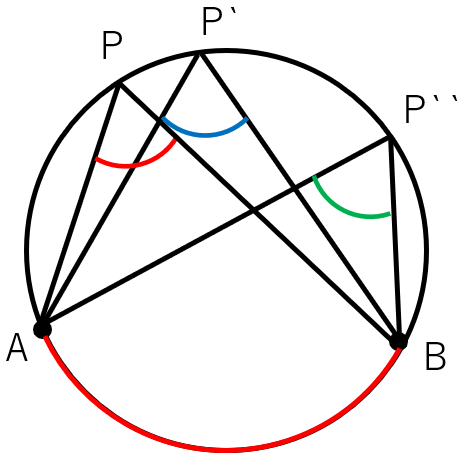
前回は「弧AB」だけに注目して見ればよかったよね。

今回は、弧ABとは別のところにある弧だけれど、弧ABと等しい弧について考えよう。

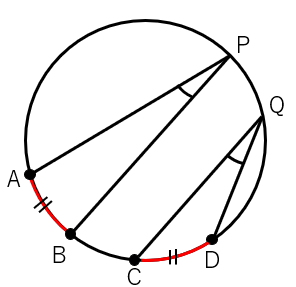
この図でイメージして欲しいのだけれど、「等しい弧」というわけなので、弧ABの部分をぐるっと円に沿ってスライドさせれば、弧CDとピッタリ重なるというわけだよね。

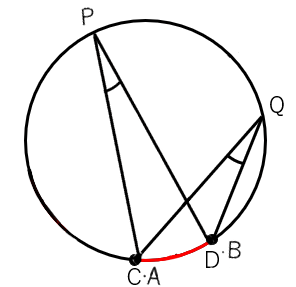
ということは、前回学習した「１つの弧に対する円周角」と同じ条件になるということだね。だから。別の等しい弧に対する円周角の大きさは変わらないんだよ。
今回の図だと、∠P＝∠Qってことだね。

それでは、練習問題にチャレンジしてみよう。

円周角と弧の関係を使った練習問題

下の図で、\(\overset{\frown}{AB}\)＝\(\overset{\frown}{CD}\)である。
ｘの角度を求めなさい。

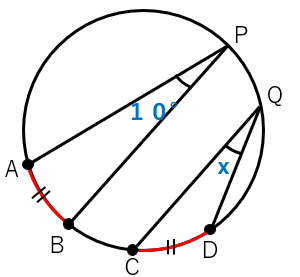
\(\overset{\frown}{AB}\)＝\(\overset{\frown}{CD}\)だから、

• ・\(\overset{\frown}{AB}\)に対する円周角∠P
• ・\(\overset{\frown}{CD}\)に対する円周角∠Q

は等しくなるよね。

だから、ｘ＝１０°と求めることができるね。

下の図で、\(\overset{\frown}{AC}\)＝２\(\overset{\frown}{CD}\)になっている。ｘの角度を求めなさい。

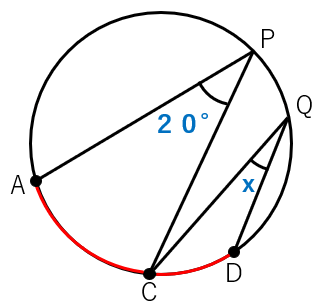
この問題では、弧ABと弧CDは等しくはないので、今度はすこし様子が違うね。
でも難しく考えることはないよ。
弧の長さが２倍になっているなら、円周角も２倍になるというだけのことなんだ。

２倍すると２０°になるのだから、ｘ＝１０°が答えになるよ。

円周角と弧の定理

「弧の長さが等しければ、円周角も等しくなる」という円周角と弧の関係がわかったね。
この関係のことを「円周角と弧の定理」というよ。

円周角と弧の定理

• 1つの円で弧の長さが等しいとき、それに対する円周角も等しい

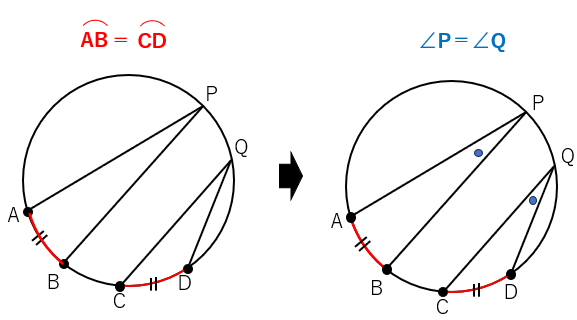
• 逆に、円周角が等しいとき、それに対する弧の長さも等しい

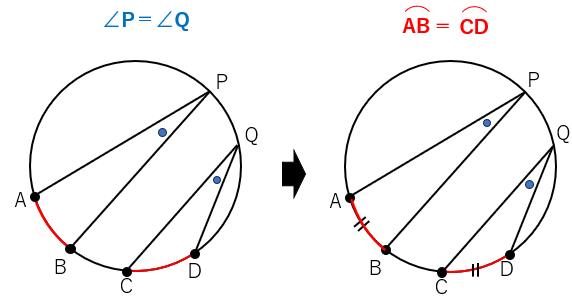
「弧の長さが等しい時、それに対する円周角も等しくなる問題」はさっきやったよね。

だから、逆の「円周角が等しい時、それに対する弧の長さも等しい」という性質を使った問題に挑戦してみよう。

円周角と弧の定理を使った練習問題

下の図で、平行な弦AD、弦BCにはさまれた\(\overset{\frown}{AB}\)と \(\overset{\frown}{CD}\)の長さが等しくなることを証明しなさい。

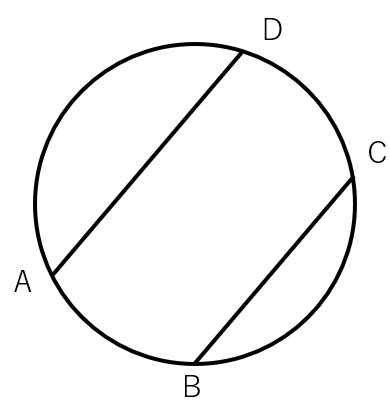
まずACを結ぼう。

弦ADと弦BCは平行だから、錯角が等しくなって、∠A＝∠Cになるよね。

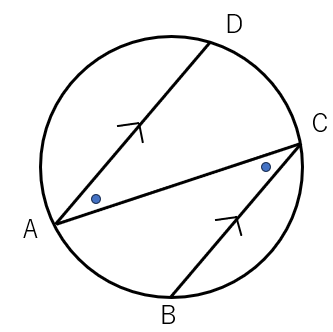
ここからが重要なポイントだよ。

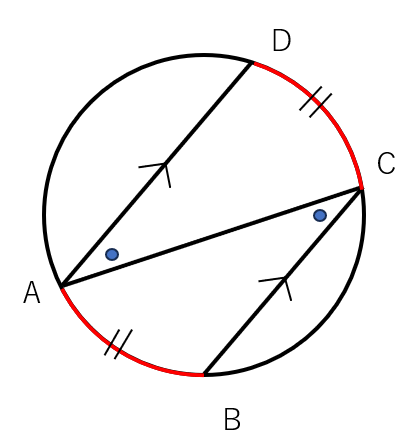
• ・∠Cは\(\overset{\frown}{AB}\)に対する円周角
• ・∠Aは\(\overset{\frown}{CD}\)に対する円周角

だよね。

∠Aと∠Cの角度は等しいから、「円周角が等しいとき、それに対する弧の長さも等しい」という性質を使うと、

\(\overset{\frown}{AB}\)＝\(\overset{\frown}{CD}\)

となることがわかるね。

直径と円周角の定理

以前に円周角と中心角について学習したよね。ちょっと復習してみよう。

円周角の定理

１つの弧に対する円周角の大きさは、その弧の中心角の大きさの半分である。
∠APB＝\(\frac{１}{２}\)∠AOB

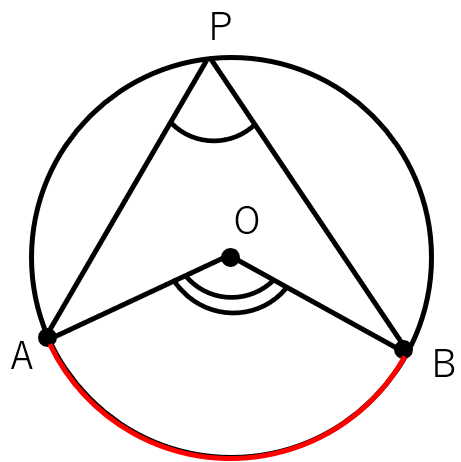
例えば、∠AOBが６０°だったら∠APBは３０°になるってことだったよね。

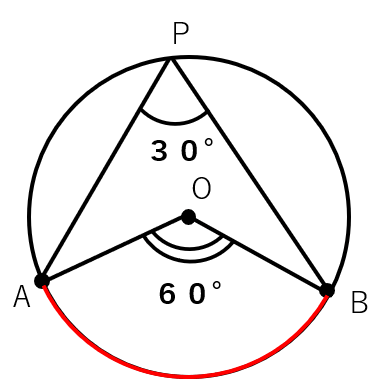
では、もし中心角が１８０°だったら円周角は何度になるか考えよう。

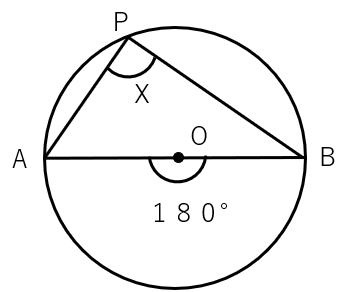
同じ弧に対する中心角の半分が円周角になるから、
円周角は１８０°÷２＝９０°と求まるね。

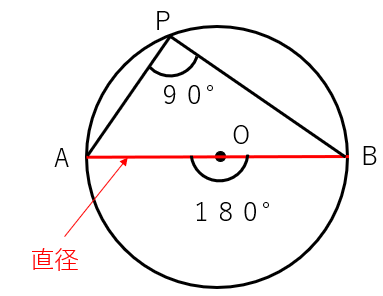
ここで気づいてほしいんだけれど、中心角が１８０°になるときって、直径しかありえないよね。

中心角が１８０°になったら、円周角は９０°になるから、次の関係が成り立つんだ。

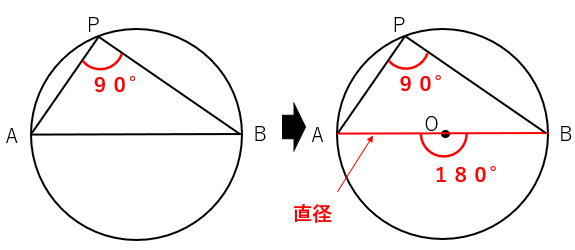
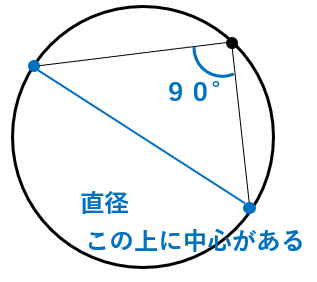
直径と円周角の定理

線分ABを直径とする円の円周上に点Pを取ると、∠APB＝９０°になる

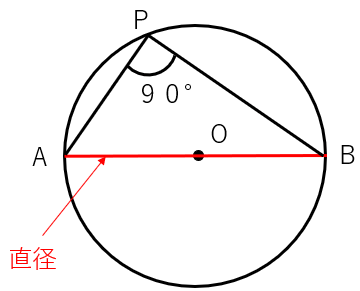
この関係を使って問題を解いてみよう。

直径と円周角の定理を使った練習問題

次の図で、線分ABが円Oの直径であるとき、ｘの角度を求めなさい。

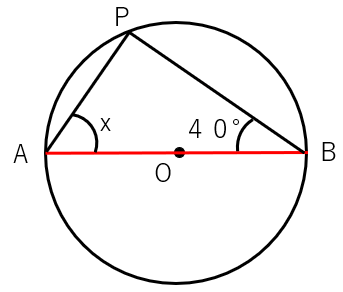
直径と円周角の関係を使うと、線分ABは直径だから中心角は１８０°になるよね。

このときの円周角∠Pは１８０°÷２＝９０°になるよね。

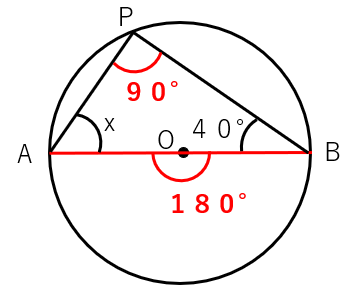
△ABPに注目すると、内角の和が１８０°になるから、残ったｘは５０°とわかるね。

直径と円周角の定理の逆

直径と円周角の定理には逆が存在するんだ。

直径と円周角の定理の逆

∠APB＝９０°ならば、線分ABは円Oの直径になる

この定理は円の中心を三角定規を使って求めるときに役立つよ。

次のような円があるとき「円の中心」を三角定規を使って求めなさい。

コンパスを使って中心を求める方法は１年生の時に学習したよね。
３年生になると三角定規だけで円の中心を求めるようになるんだよ。

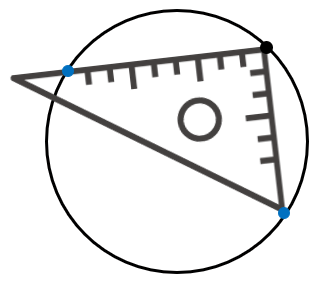
STEP１　三角定規の直角部分が円周に重なるように置いて、円周と交わる点を２つ取る

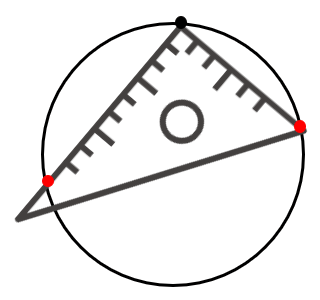
STEP２　赤い点同士を結ぶ

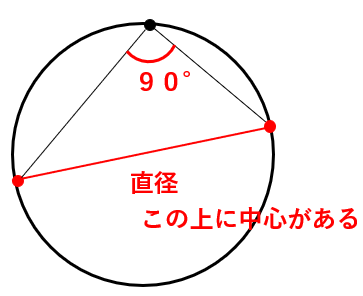
結ぶと次のようになって、円周角が９０°だから、赤線は直径ということがわかるよ。

つまり、円の中心は赤線の上にあるってことだね

STEP３　さらに三角定規の直角部分が円周に重なるように置いて、円周と交わる点を２つ取る

STEP４　青い点同士を結ぶ

結ぶと次のようになって、円周角が９０°だから、青線は直径ってことがわかるよ。

つまり、円の中心は青線の上にあるってことだね。

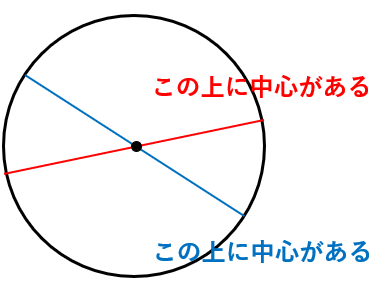
STEP５　赤線と青線が交わったところが中心

赤線も直径、青線も直径でどちらともの上に中心があるってことになるよ。

だから交わっているところが中心になるね。

「円周角と弧の定理」「直径と円周角の定理」まとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。

1. もっちゃん より:

   2025年7月26日 11:33 AM

   また、教えてください。

   円周を全て適当な長さの円弧で分割した時、各円弧の中心角の総和は360度なのでその円周角の総和は180度となって、円周角は中心角の半分になるということとつじつまが合います。

   友達に聞かれてよくわからなくなったのですが、一つの円弧の中心角がどんどん大きくなって360度に近づくにつれ、円周角も限りなく180度に近づくのがわかります。
   でも、中心角が360度になってしまうと、円弧の両端と円周角の頂点は完全に一つの点になってしまう…円周角は出来ない？？
   このことは0,999……=1になるという無限の考え方と同じで、179.999…..=180度にするんだろうなという話で終わっているのですが？？

   返信
   • yumineko より:

     2025年7月26日 1:21 PM

     もっちゃんさんの疑問は、

     ・円周角と中心角の関係（円周角は中心角の半分）の基本
     ・中心角が360度に近づくにつれて、円周角はどうなるのか？
     ・中心角がちょうど360度になってしまったときの円周角の扱い
     ・「179.999… = 180度」という無限の考え方との関連

     という４つのポイントに整理できますね。一つずつ、分かりやすく説明していきます。

     円周角と中心角の関係について（基本）
     まず、もっちゃんさんの基本的な理解は正しいです。
     中心角: 円の中心を頂点とし、円周上の2点を通る2本の線分（半径）が作る角です。
     円周角: 円周上の1点を頂点とし、円周上の他の2点を通る2本の弦が作る角です。
     関係: 同じ円弧に対する円周角の大きさは、その円弧に対する中心角の大きさの半分になります。
     （中心角） = 2 × （円周角）

     もっちゃんさんがおっしゃるように、円周をいくつかの円弧に分割して、それぞれの中心角を足すと360度になるのはその通りです。そして、それぞれの円弧に対する円周角も、中心角の半分なので、それらを足し合わせると必ず180度になります。これは、円周角の定理の基本的な性質ですね。

     中心角が360度に近づくとき、円周角はどうなる？
     ここからが、もっちゃんさんの核心的な疑問ですね。
     円周をたくさんの小さな円弧に分割していくと、それぞれの中心角は小さくなります。
     しかし、逆に 「円弧がどんどん大きくなって、中心角が360度に近づく」 という状況を考えてみましょう。
     たとえば、円周を「2つの円弧」に分割するのではなく、「1つの円弧」だけを考えた場合を想像してみてください。
     中心角が、例えば270度になったとします。
     このとき、円周上の頂点A、B、Cがあるとします。中心O、弧ABに対する円周角は∠ACBです。
     中心角が360度に近づくということは、円弧が円周全体に近づいていく、ということです。
     もし、中心角が360度に近い角度（例えば359度）だったとしましょう。
     このとき、円周角の頂点（仮にCとします）は、中心角を作る2つの半径の「すぐ近く」にあります。
     中心角が360度に近いということは、円周角の頂点Cは、中心角を作る2つの半径の「始点」と「終点」がほぼ重なる、円周上の「ある一点」に非常に近づいている状態です。
     中心角が360度に近づくにつれて、円周角も中心角の半分なので、180度に近づきます。
     このときの円周角の頂点は、円周上のどこか一点に位置しますが、中心角が360度に近づくにつれて、その円周角の「両端」となる点（中心角を作る2つの半径が円周と交わる点）が、円周上の「一点」にどんどん近づいていくイメージです。

     中心角がちょうど360度になってしまったとき、円周角はできない？
     もっちゃんさんのご指摘は鋭いです。
     中心角がちょうど360度になるということは、円周上の2点（中心角の始点と終点）が、円周上の「同じ一点」に重なってしまう ということになります。
     この場合、円周角の定義を厳密に考えると、「円周上の2点を通る弦」 が必要ですが、2点が一点に重なってしまうと、弦は定義できなくなります。
     また、中心角が360度ということは、円周角の頂点も、中心角を作る2つの半径の「始点」と「終点」が重なる円周上の「一点」に位置することになります。
     そうなると、円周角の「頂点」と、円周角を作る「2つの弦の端」がすべて同じ点になってしまうため、「角」として意味をなさなくなります。

     数学では、このような「極限の状態」や「定義が曖昧になる場合」は、「定義されない」 とする場合があります。

     「179.999… = 180度」という無限の考え方との関連
     ここでもっちゃんさんが「179.999…..=180度にするんだろうな」とおっしゃったのは、まさにこの「極限」という考え方とつながります。
     数学では、ある値に限りなく近づくことを「極限」と言います。
     中心角が360度に「限りなく近づく」とき、円周角は180度に「限りなく近づきます」。
     この「限りなく近づく」という状態を考えると、数学的には180度とみなすことができるのです。
     ただし、中心角が 「ちょうど360度」 になった瞬間に、円周角の定義から外れてしまうため、「179.999…度」のように「限りなく180度に近づく」という状態とは少し異なります。

     「円周角はできない？」という疑問について、もう少し補足すると、
     中心角が360度になった場合、円周角の頂点が一点に集まってしまうため、私たちがイメージする「角」としては定義されなくなります。
     しかし、数学では、こうした「境界線」のような状態を考えるときに、「極限」という考え方を使って、その値に「限りなく近い」状態を考えることがあります。
     円周角の定理を考える上では、「中心角が360度未満の範囲」で考えていることがほとんどです。
     もし「中心角が360度」という状況をあえて考えるならば、それは「円周角」というよりは、線分が一点に重なった「退化（たいか）した状態」と考えることもできます。
     もっちゃんさんが友達との会話で「179.999…..=180度にするんだろうな」という結論になったのは、「中心角が360度に近づく」という現象から、円周角が180度に近づくことの「極限」としての意味合いにたどりついたという点で、非常に鋭い考えだと思います。

     返信
2. もっちゃん より:

   2025年7月26日 3:16 PM

   ありがとうございます。
   先生の話をまとめると、次の理解で良いのでしょうか？

   極限の世界として１つの円弧の中心角が360度に限りなく近づく時、円周角は179.999… = 180度と考えることが出来るが、１つの円弧の中心角が360度となるときは、円周角は定義されない。

   返信
   • yumineko より:

     2025年7月26日 3:26 PM

     もっちゃんさん、ご自身の言葉でまとめくださりありがとうございます。
     中心角が360度に近づく場合と、ちょうど360度になった場合の区別を、明確に理解されているのがよく分かります。
     このまとめ方で良いと思います！

     返信
     • もっちゃん より:

       2025年7月26日 5:10 PM

       先生のこのサイトを知る事が出来てとてもよかった思ってます。これからもよろしくお願いいたします。

       返信
       • yumineko より:

         2025年7月26日 11:28 PM

         そんな風に言っていただけてとても嬉しいです！
         ありがとうございます。

         返信
3. もっちゃん より:

   2025年7月27日 10:15 AM

   このページを読みながらちょっと思い出したこと

   1、円周角と弧の定理
   　練習問題において四角形ABCDは台形であり、また円周角と弧の定理の関係から円に内接する台形ABCDは必ず等脚台形になる。
   ２、直径と円周角の定理
   　円に内接する長方形の対角線はその円の直径になる。

   返信