「ｙはｘの二乗に比例する」関数の変化の割合の求め方・変域とは？

中学３年生の数学で学習する「ｙはｘの二乗に比例する関数（y=ax²）」について、ｘが増加に対して、ｙがどのように増加するかの「変化の割合」がどういう仕組みになっているのか、変化の割合の求め方・変域の求め方をわかりやすく解説するよ。

「ｙはｘの二乗に比例する」関数の 変化の割合の求め方・変域とは？のPDF（10枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• y=ax²の値の変化
• y=ax²の変化の割合の求め方
• y=ax2の変域
• まとめ

y=ax²の値の変化

「ｙはｘの二乗に比例する関数（y=ax²）」の値が、どのように変化していくのか見ていこう。

y=2x²の「ｘ」と「ｙ」の対応表を作成してみたよ。

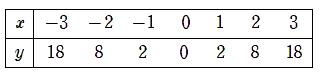
この対応表を見ると、「x=0」からｘが１ずつ増えると、ｙは２、６、１０と増えていっているよね。

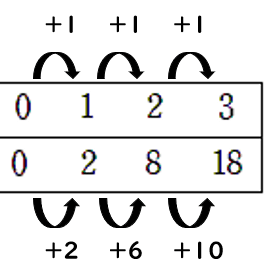
ｙの増え方はずっと同じでではないよね。

ずっと同じことを「一定」というから、
「y=ax²の値の変化は一定ではない」といえるね。

２年生で勉強した一次関数「y=ax+b」の値の変化はどうだったのか復習してみよう。

一次関数「y=ax+b」の値の変化

一次関数「y=2x+1」の「ｘ」と「ｙ」の対応表を確認してみよう。

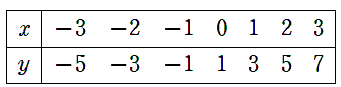
対応表を見ると「x=0」からｘが１ずつ増えると、ｙは２ずつ増えているよね。

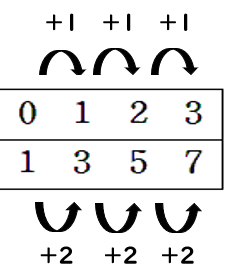
ｙは２ずつ増えているから、「y=ax+b」の値の変化は一定だとわかるね。

y=ax²の変化の割合の求め方

「変化の割合」という言葉を覚えているかな？
変化の割合とは、「どのくらい変化したか」を表すものだったよね。

ｙはｘの二乗に比例する関数「y=2x²」の変化の割合\(\frac{yの増加量}{xの増加量}\)は、次のようになるよ。

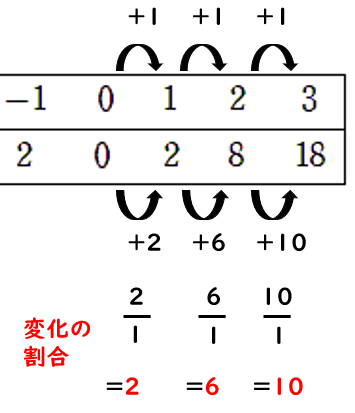
変化の割合はだんだんと大きくなっていて、一定ではないことがわかるね。

ｙはｘの二乗に比例する関数（y=ax²）の変化の割合は、ｘの範囲によって変わってくるんだ。
実際に問題で確かめてみよう.

y=ax²の変化の割合を求める問題

変化の割合は、\(\frac{yの増加量}{xの増加量}\)で求めることができるので

ｘとｙの対応表を考えてみよう。

y=3x²で

x=1のとき、
y=3x²
=3×x²
=3×1²
=3×1
=3

x=4のとき、
y=3x²
=3×x²
=3×4²
=3×16
=48

ｘとｙの対応表を作ってみよう。関係のないところは「…」と書いてあるよ。

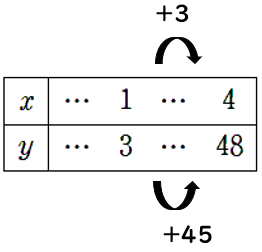
対応表から、ｘの増加量＝＋３、ｙの増加量＝＋４５とわかるから、

=\(\frac{yの増加量}{xの増加量}\)
=\(\frac{+45}{+3}\)
=15

変化の割合は「15」と求めることができたね。

じゃあ次に、ｘの範囲を変えてみるよ。

変化の割合は\(\frac{yの増加量}{xの増加量}\)で求めることができるので、

ｘとｙの対応表を考えてみよう。

y=3x²で

x=-2のとき、
y=3x²
=3×x²
=3×(-2)²
=3×4
=12

x=1のとき、
y=3x²
=3×x²
=3×1²
=3×1
=3

ｘとｙの対応表を作ってみよう。関係のないところは「…」と書いてあるよ。

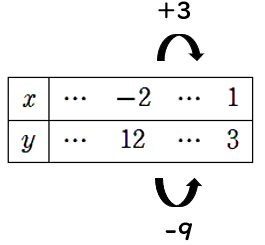
対応表から、ｘの増加量＝＋３、ｙの増加量＝－９とわかるので、

=\(\frac{yの増加量}{xの増加量}\)
=\(\frac{-9}{+3}\)
=-3

変化の割合は「-3」と求めることができたね。

ｙはｘの二乗に比例する関数（y=ax²）の変化の割合は、ｘの範囲によって変わってくることをしっかり覚えておこう。

一次関数「y=ax+b」の変化の割合

一次関数の変化の割合はどうなっていうのか、復習もかねて確認しておこう。

y=2x+1の変化の割合\(\frac{yの増加量}{xの増加量}\)は次のようになるよ。

変化の割合はずっと「２」になるから、一定だとわかるね。

一次関数の変化の割合は一定になるよ。

y=ax²の変域

ｙはｘの二乗に比例する関数の変域を考えてみよう。

「変域」とは、「範囲のこと」だと思っていればＯＫだよ。
変域について解説しているページもあるので、参考にしてね。

まず、y=x²のグラフの形を思い出してみよう。

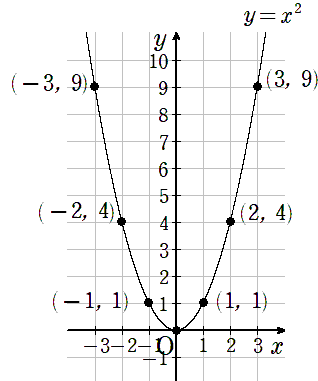
(1)

1≦x≦3の範囲だけグラフを書いてみると次のようになるよ。

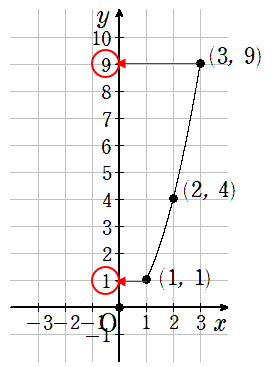
ｙの値は、y=x²の式にｘを代入してそのつど求めることができるね。

ｙの最小値はｙ＝１のとき、
ｙの最大値はｙ＝９のときだから

1≦y≦9

とｙの変域が求まるよ。

(2)

-2≦x≦1の範囲だけグラフを書いてみると次のようになるよ。

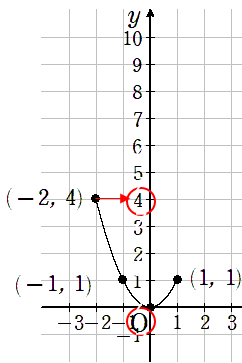
ｙの最小値はｙ＝０のとき、
ｙの最大値はｙ＝４のときだから

0≦y≦4

とｙの変域が求まるよ。

よくある間違い

y=x²でxの変域が-2≦x≦1のときのｙの変域を求める問題は間違えやすいので、注意が必要だよ。

なぜなら、ｘの変域に「０」が含まれているから。
（－２から１の範囲に、「０」がふくまれているよね）

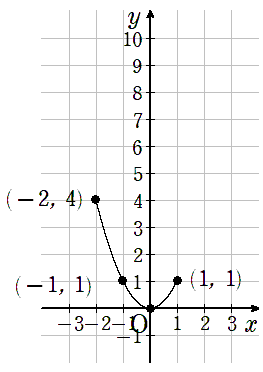
最大値はｙ＝４のときだというのは間違えようがないんだけれど、問題は最小値。

グラフを書けば、最小値はｘが「０」のときのｙ＝０のときだとわかるんだけれど、
グラフを書かずに式と変域だけで見てしまうと、つい最小値はｘ＝１のときのｙ＝１と早とちりしてしまうんだよ。

ミスをふせぐために、ｙはｘの二乗に比例する関数（y=ax²）のｘ変域が「０」をはさむ場合は、簡単でいいのでグラフを書いてｙの変域を確かめるのが確実で安全だね。

「ｙはｘの二乗に比例する関数の変化の割合・変域」まとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。