「二次方程式の解の公式」とは?解の公式の証明と問題の解き方
中学3年生の数学で学習する「二次方程式の解の公式」について、解の公式とはどんなものか、なぜ学習する必要があるのか、二次方程式の解の公式がなぜ成り立つのか、解の公式を使って問題を解く方法をわかりやすく解説するよ。
二次方程式の解の公式とは
「二次方程式の解の公式」だなんて言葉だけを聞くと、なんだかとっても難しそうで身構えてしまうよね。
まず、「二次方程式の解の公式」とはなんなのか、何のためにそれを学ぶのかを説明するよ。
まず「公式」についてなんだけれど、今までも公式はいろいろなものを学習してきたよね。
たとえば、「円の面積を求める公式」。
円の面を求める公式は、「πr2」だね。
この「円の面積を求める公式」を覚えてしまえば、あとは円の半径(r)が分かれば、すぐに円の面積を計算することができて、とても便利だよね。
公式は、ざっくり説明すると、「空欄(文字になっているところ)に必要な情報を当てはめれば、答えが分かってしまう便利なツール」というイメージかな。
さて、二次方程式の話に戻って、二次方程式の一般形は、「ax²+bx+c=0」だね。
問題では、たとえば「二次方程式 2x2+3x+1=0 を解きなさい」なんていうように登場するよね。
これまで、xがいくつになるかを解くために、式の部分を平方根で考えてみたり、因数分解を使って考えてみたりしてきたよね。
でも、これらの方法って、たまたま平方根で考えることができる形だったとか、たまたま因数分解を使って考えることができる形だったときにしか通用しないよね。
では、それらの方法が通用しないとき、どうすればいいのかというと、そこで大活躍するのが「解の公式」なんだよ。
「二次方程式の解の公式」は、どんな問題でも必ず通用する必殺アイテムなんだ。
「二次方程式の解の公式」を覚えておけば、「ax²+bx+c=0」の「a」「b」「c」が分かれば、その公式に当てはめてあげることで、xがいくつか分かってしまうんだよ。
そんな便利アイテム「二次方程式の解の公式」を紹介するよ。
二次方程式の解の公式
x=\(\frac{-b±\sqrt{b^2-4ac}}{2a}\)
なにこれ!!!
初めて見ると、びっくりしてしまうよね。
たしかにかなり複雑な公式なんだけれど、バンバン使うし、なんなら高校数学でも使うので、なんとしても絶対に覚えよう。
解の公式の覚え方について
解の公式を覚えるための語呂合わせもいくつかあるのだけれど、みんな言うのは「結局そのまま覚えるのが一番速い」ということ。
この公式、たしかに複雑だけれど、口に出して見ると結構リズムが良いというか、何度も何度も口ずさむうちに、案外覚えてしまったりするよ。
「にーえーぶんのまいなすびーぷらすまいなするーとびーにじょうまいなすよんえーしー」
これを地道に復唱してみよう。かけざんの九九と同じ感覚だね。
なんだか呪文みたいで楽しいという意見もあるよ。せっかくなら楽しんでしまおう!
二次方程式「ax²+bx+c=0」を解いてみよう
二次方程式の解の公式はx=\(\frac{-b±\sqrt{b^2-4ac}}{2a}\)だと紹介したけれど、「一体なんでこんな公式になるの?」と思うかもしれないね。
公式は、「なぜその公式が成り立つのか」を考えることも大切だよ。
そこで、ここではなぜ二次方程式の解がx=\(\frac{-b±\sqrt{b^2-4ac}}{2a}\)となるのか、確かめてみよう。
どうやって確かめるのかというと、「ax²+bx+c=0」を、xについて解いてみればいいんだ。
では、ここから実際に「ax²+bx+c=0」を解いていくよ。
「ax²+bx+c=0」を解くので、数字ではなく文字で考えるから計算は結構ややこしくなってしまうよ。
ゆっくりひとつずつ確認していってね。
➀ax²+bx+c=0の両辺をaで割る
以前、x2+ax+b=0を(x+○)2=△みたいな形にしたよね。(平方完成)
同じようにやるためには「ax²+bx+c=0」の両辺を「a」で割って、x2の係数を1にしよう。
まず、x2の係数「a」がじゃまだから、両辺を「a」で割ろう。
(ax²+bx+c)÷a=0÷a
x2+\(\frac{b}{a}\)x+\(\frac{c}{a}\)=0
x2の係数が「1」になったね。
➁(x+○)2=△の形にする
x2+\(\frac{b}{a}\)x+\(\frac{c}{a}\)=0を(x+○)2=△にするために、まずは+\(\frac{c}{a}\)を右辺に移項しよう。
x2+\(\frac{b}{a}\)x+\(\frac{c}{a}\)=0
x2+\(\frac{b}{a}\)x =-\(\frac{c}{a}\)
ここまでできたら次がすごく重要。
(x+○)2=△にするために、両辺にある数を足すんだけどいくつかわかるかな?
答えは\(\frac{b^2}{4a^2}\)を両辺に足すよ。
以前学習した(x+○)2=△のポイントを復習してみよう。
(x+○)2=△の形にするポイント
x2+ax+b=0の両辺に「aを2で割った数の2乗」を足す。
つまり「xの前の係数を2で割った数の2乗」を足すってことだったよね。
今回の問題「x2+\(\frac{b}{a}\)x =-\(\frac{c}{a}\)」でいったら
- xの前の係数は\(\frac{b}{a}\)
- xの前の係数を2で割った数は、\(\frac{b}{a}\)÷2=\(\frac{b}{2a}\)
- xの前の係数を2で割った数の2乗は、(\(\frac{b}{2a}\))2=\(\frac{b^2}{4a^2}\)
になるよ。
だからx2+\(\frac{b}{a}\)x =-\(\frac{c}{a}\)の両辺に\(\frac{b^2}{4a^2}\)を足してみよう。
x2+\(\frac{b}{a}\)x=-\(\frac{c}{a}\)
x2+\(\frac{b}{a}\)x +\(\frac{b^2}{4a^2}\)=-\(\frac{c}{a}\)+\(\frac{b^2}{4a^2}\)
ここまでついてこられたかな?すごく複雑な式になっているね。
(左辺)と(右辺)に分けて考えよう。
(左辺)=x2+\(\frac{b}{a}\)x +\(\frac{b^2}{4a^2}\)
x2+\(\frac{b}{a}\)x +\(\frac{b^2}{4a^2}\)は(x+○)2の形にできるんだけど、○に入る文字式はわかるかな?
○に入る式は「xの係数を2で割ったもの」だから、\(\frac{b}{a}\)÷2=\(\frac{b}{2a}\)が入るよ。
だから
(左辺)
=x2+\(\frac{b}{a}\)x +\(\frac{b^2}{4a^2}\)
=(x+\(\frac{b}{2a}\))2
になるよ。
(右辺)=-\(\frac{c}{a}\)+\(\frac{b^2}{4a^2}\)
2つの分数の足し算を考えよう。
分母は「a」と「4a2」だから、「4a2」にそろえよう。
そのために
-\(\frac{c}{a}\)の分母と分子に「4a」をかけよう
=-\(\frac{c×4a}{a×4a}\)
=-\(\frac{4ac}{4a^2}\)
だから
(右辺)
=-\(\frac{c}{a}\)+\(\frac{b^2}{4a^2}\)
=-\(\frac{4ac}{4a^2}\)+\(\frac{b^2}{4a^2}\) ←分母が同じだから1つの分数にまとめるよ。
=\(\frac{-4ac+b^2}{4a^2}\) ←分子の-4acとb2の順番を入れ替えるよ。
=\(\frac{b^2-4ac}{4a^2}\)
③(x+○)2=△の形にする
(左辺)と(右辺)の計算から
x2+\(\frac{b}{a}\)x +\(\frac{b^2}{4a^2}\)=-\(\frac{c}{a}\)+\(\frac{b^2}{4a^2}\)は次のように表せるよ。
x2+\(\frac{b}{a}\)x +\(\frac{b^2}{4a^2}\)=-\(\frac{c}{a}\)+\(\frac{b^2}{4a^2}\)
(x+\(\frac{b}{2a}\))2=\(\frac{b^2-4ac}{4a^2}\)
無事に(x+○)2=△の形に変形することができたね。
xの値を求める
いよいよxの値を求めてみるよ。その前にちょっと復習をしてみよう。
ちょっと復習
(x+3)2=5の解を求めよ。
(x+3)をAとおいて
A2=5
Aは2乗して5になる数なんだけど、整数では存在しないからルートを使って
A=-\(\sqrt{5}\)
A=\(\sqrt{5}\)
と求めるんだったよね。
Aってx+3のことだから、もとにもどして
x+3=-\(\sqrt{5}\)
x+3=\(\sqrt{5}\)
になるから「3」を移項して
x=-\(\sqrt{5}\)-3
x=\(\sqrt{5}\)-3
が解になるんだったよね。
本題にもどって
(x+\(\frac{b}{2a}\))2=\(\frac{b^2-4ac}{4a^2}\)のxの値を求めよう。
(左辺)の「x+\(\frac{b}{2a}\)」を「A」と置くと
(x+\(\frac{b}{2a}\))2=\(\frac{b^2-4ac}{4a^2}\)
A2=\(\frac{b^2-4ac}{4a^2}\)
Aは2乗して、\(\frac{b^2-4ac}{4a^2}\)になる数なんだけど、整数では存在しないからルートを使おう。
A2=\(\frac{b^2-4ac}{4a^2}\)
A=±\(\sqrt{\frac{b^2-4ac}{4a^2}}\) ←「±」というのは、+と-を合わせた表し方だよ。
あえて、ルートを分母と分子にわけると次のようになるよ。
A=±\(\sqrt{\frac{b^2-4ac}{4a^2}}\)
A=±\(\frac{\sqrt{b^2-4ac}}{\sqrt{4a^2}}\)
\(\sqrt{4a^2}\)は
\(\sqrt{4a^2}\)
=\(\sqrt{2a×2a}\)
だからルートを外すことができて、「2a」になるよね。
だから
A=±\(\frac{\sqrt{b^2-4ac}}{\sqrt{4a^2}}\)
A=±\(\frac{\sqrt{b^2-4ac}}{2a}\)
と表せるよ。
「A」を「x+\(\frac{b}{2a}\)」にもどそう
x+\(\frac{b}{2a}\)=±\(\frac{\sqrt{b^2-4ac}}{2a}\)
xの値を求めたいので、(左辺)の+\(\frac{b}{2a}\)を移項して
x=-\(\frac{b}{2a}\)±\(\frac{\sqrt{b^2-4ac}}{2a}\)
-\(\frac{b}{2a}\)の「-(マイナス)」を分子にもってくると
x=\(\frac{-b}{2a}\)±\(\frac{\sqrt{b^2-4ac}}{2a}\)
(右辺)は2つとも分母が「2a」だから1つの分数にして
x=\(\frac{-b}{2a}\)±\(\frac{\sqrt{b^2-4ac}}{2a}\)
x=\(\frac{-b±\sqrt{b^2-4ac}}{2a}\)
とxの値を求めることができたね。
解の公式を使って2次方程式を解いてみよう
さっき、ax²+bx+c=0の解が求まったね。
どんな2次方程式でも形は「ax²+bx+c=0」になるから、その解は
x=\(\frac{-b±\sqrt{b^2-4ac}}{2a}\)
と表されるんだよ。
実際にどのように解の公式を使うか問題を使って確かめてみよう。
(1)2x2+3x+1=0を解の公式を使って解きなさい。
ax²+bx+c=0と比べると
a=2、b=3、c=1であることがわかるね。
この3つの値を解の公式に代入しよう。
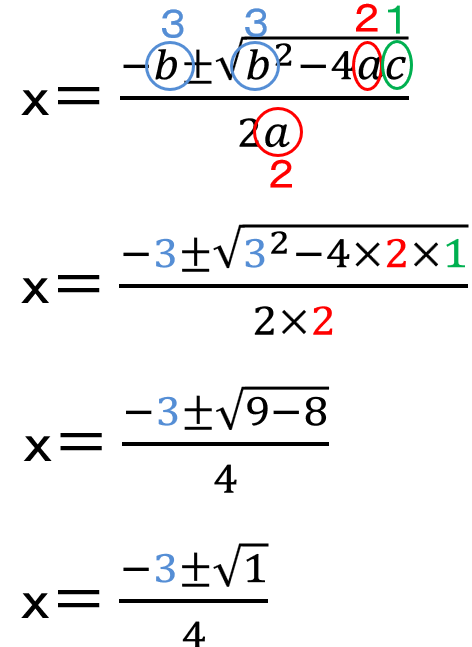
\(\sqrt{1}\)=1になるから、もう少し計算することができるね。

(2)x2-3x+1=0を解の公式を使って解きなさい。
ax²+bx+c=0と比べると
a=1、b=-3、c=1であることがわかるね。
この3つの値を解の公式に代入しよう。
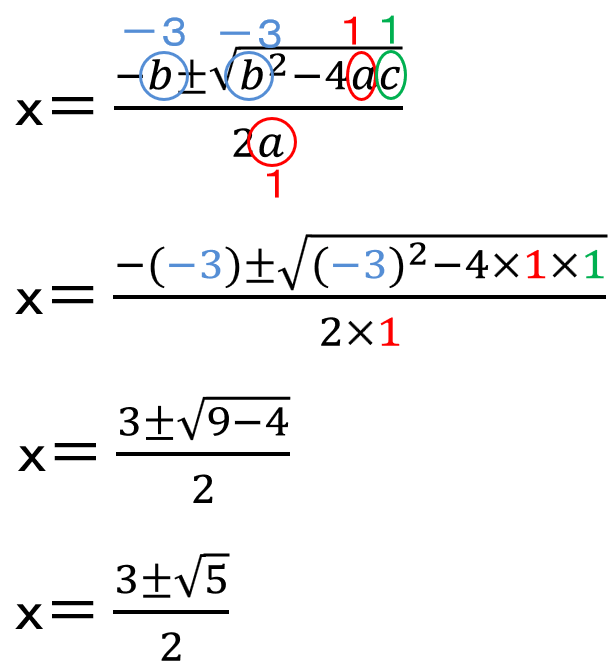
解の公式で気を付けること
・「-(マイナス)」を代入するときは、かっこをつける。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。

-
至急!解の公式いい覚え方ありますか?語呂合わせで、お願いします!



至急❗️解の公式いい覚え方ありますか?語呂合わせで!お願いします